An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
![An infinite cylindrical wire of radius R and having current density varying with its radius r as, J = J(0)[1-(r//R)]. Then answer the following questions. Graph between the magnetic field and radius is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_MCA_E01_140_Q01.png)
Graph between the magnetic field and radius is
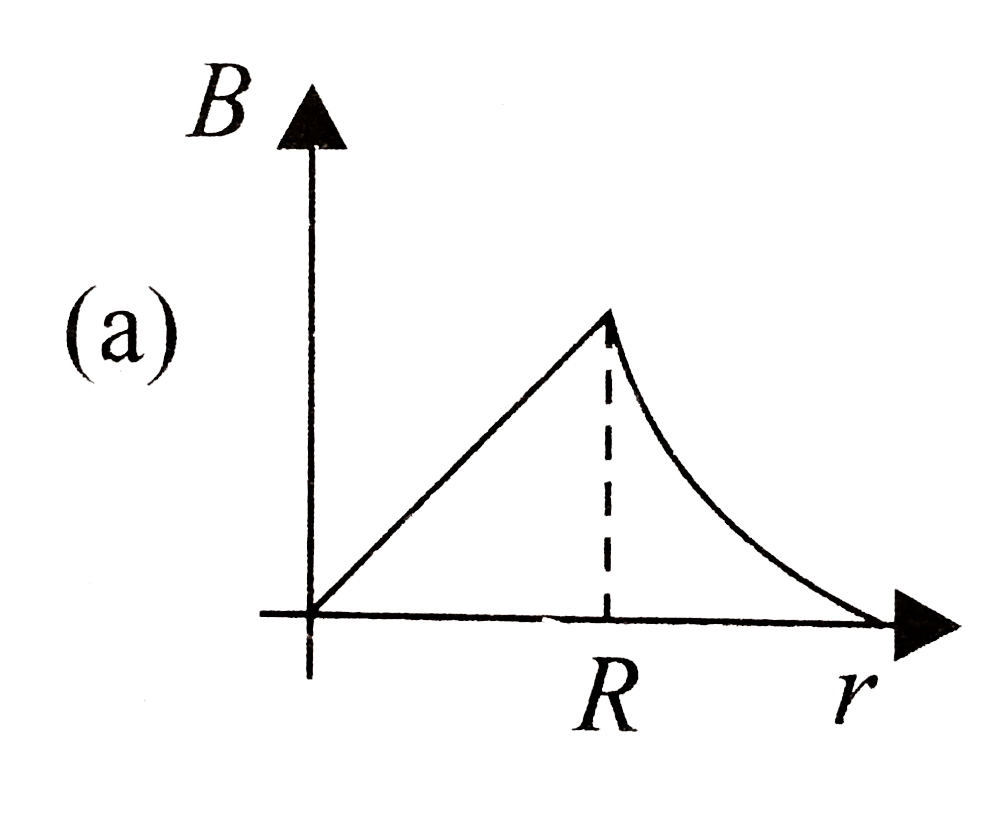
The correct Answer is:D
Current with in radius r:I=∫rJdA
⇒I=∫r0J0[1−RR]2πrdr=2πj0[r22−r33R]
Apply ampere's law B2πr=μ0I
B2πr=μ02πJ0(r22−r33R)⇒B=μ0J0[r2−r23R]
to find max B: dBdr=0⇒r=3R/4
Bmax=μ0J90[3R/42−(3R/4)23r]=3R16μ0J0.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Multiple Correct
Explore 34 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- Moving charges and magnetismBook:CENGAGE PHYSICSChapter:Moving charges and magnetismExercise:Question Bank
Explore 20 Videos
Similar Questions
A non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View Solution
Knowledge Check
An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Magnitude of maximum magnetic field isAJ0R6μ0B316J0Rμ0C516J0Rμ0D56J0Rμ0An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Position where magnetic field strength is maximum.ARB3R/4Cr/2DR/4A cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
AπJ0R22B2πJ0R23C4πJ0R23Dnone of these
There are two separate long cylindrical wires having uniform current density. The radius of one of the wires is twice that of the other. The fig. shows the plot of magni- tude of magnetic field intensity versus radial distance (r) from their axis. The curved parts of the two graphs are overlapping. Find the ratio B1:B2.

View SolutionAn infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
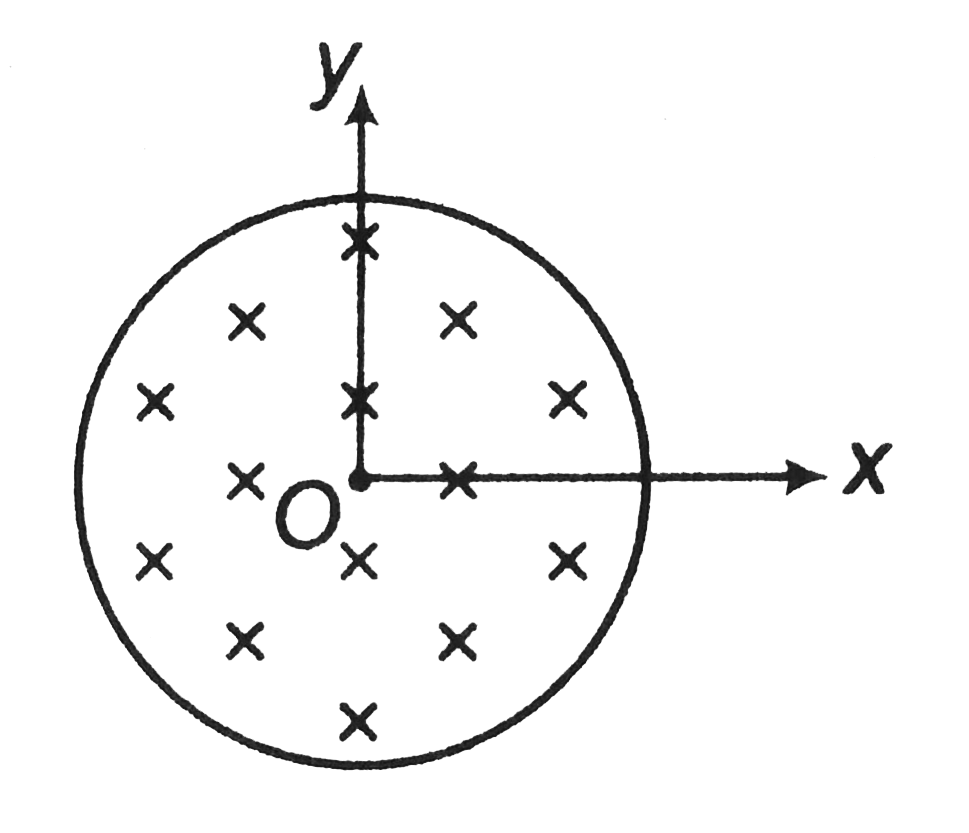
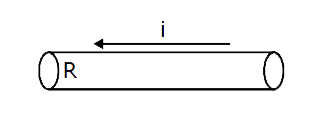
View SolutionA long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r1(r1<R) is
View SolutionConsider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=αr where a is a constant. Find the magnetic field for inside and outside prints.
View Solution

