ABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m
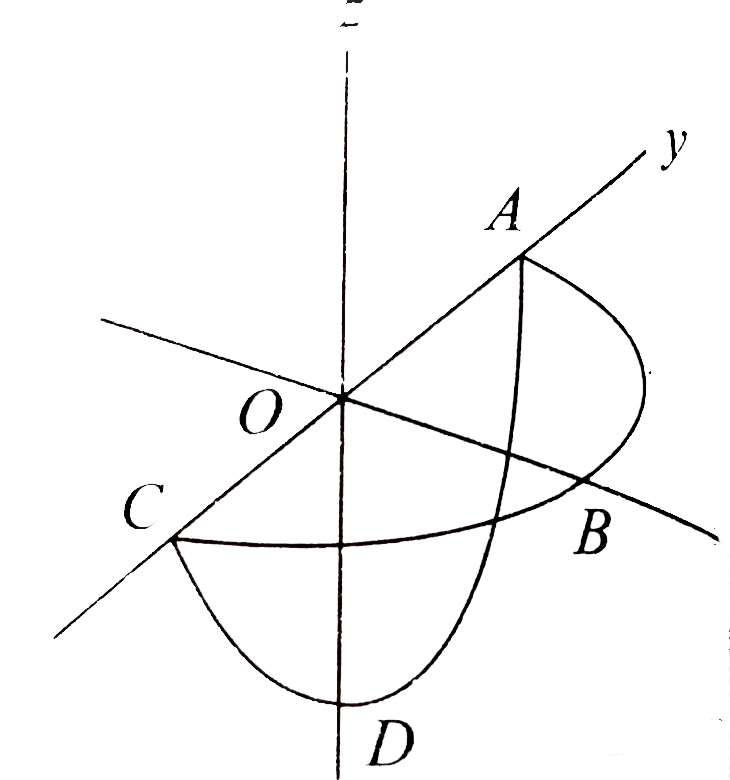
If →B be directed along (+→i−→k) and decreases at the rate of 10−2Tesla/second, the magnitude and the sense of the induced emf in the loop, as seen along the magnetic field direction will be
zero
5π4√2 mV in the counterclockwise sense
5π4√2 mV in the clockwise sense
5π2√2mV in the clockwise sense.
The correct Answer is:D
it is given →B=(→i−→k√2)|B|and∣∣∣dBdt∣∣∣=10−2T/s
It is obvious that B is directed perpendicular to y-axis. Components BxandBz of the field B are Bx=B√2andBz=−B√2.
Then the flux (at instant t) through ABC=ϕ1=(πa22)Bz

Hence emf e1 induced in loop ABC is
e1=−dϕ1dt=−πa22⋅dBzdt=+πa22√2(dBdt)
This emf will be directed clockwise (looking along negative z axis) −−−→ABC.
Similarly the flux (at instant t) throght ADC=(ϕ2=)=πa22Bx.
Hence emf e2 induced in loop ADC is
e2=−dϕ2dt=−πa22dBxdt=−πa22√2(dBdt)
this emf will be directed clockwise (looking along positive x axis ) −−−→CDA.
It is easy to see that these two emfs along the two semicircles will add up.
Hence induced emf in the closed loop will be
e=|e1|+|e2|=πa22√2dBdt+πa22√2dBdt
It is given dBdt=10−2T/s and a=0.5m.
Hence e=π(0.5)2√2⋅10−2V=5π2√2×10−3V=5π2√2mV
This will be in clokwise sence, when looking along B.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
ABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m
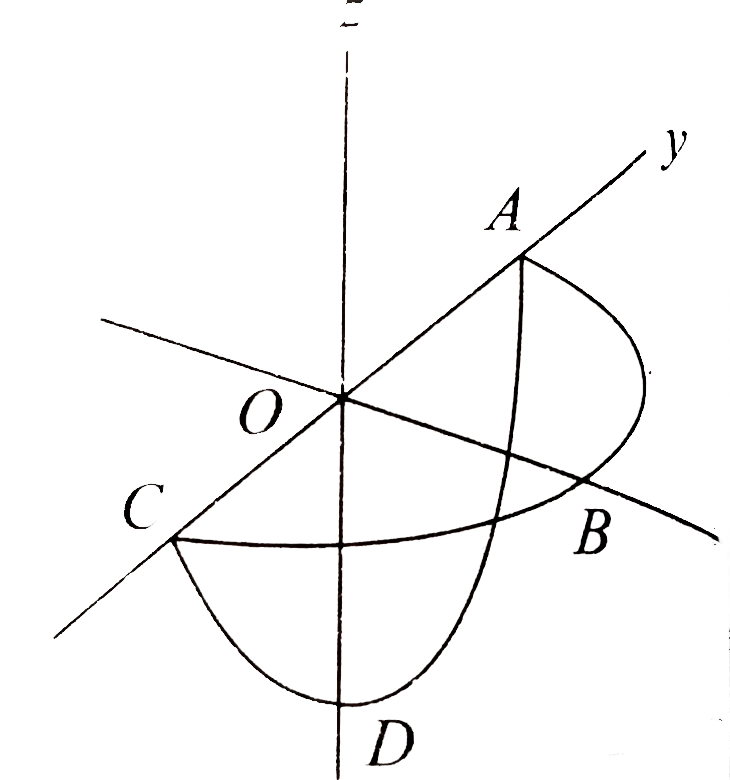
If →B be directed along the vector (→i−→j) and decreases at the rate of 10−2Teslasecond. The magnitude and sense of the induced emf in the loop as seen along the positive x-axis will beAzeroB5π4√2 mV in the counterclockwise senseC5π4√2 mV in the clockwise senseD5π2√2mV in the clockwise sense.ABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m
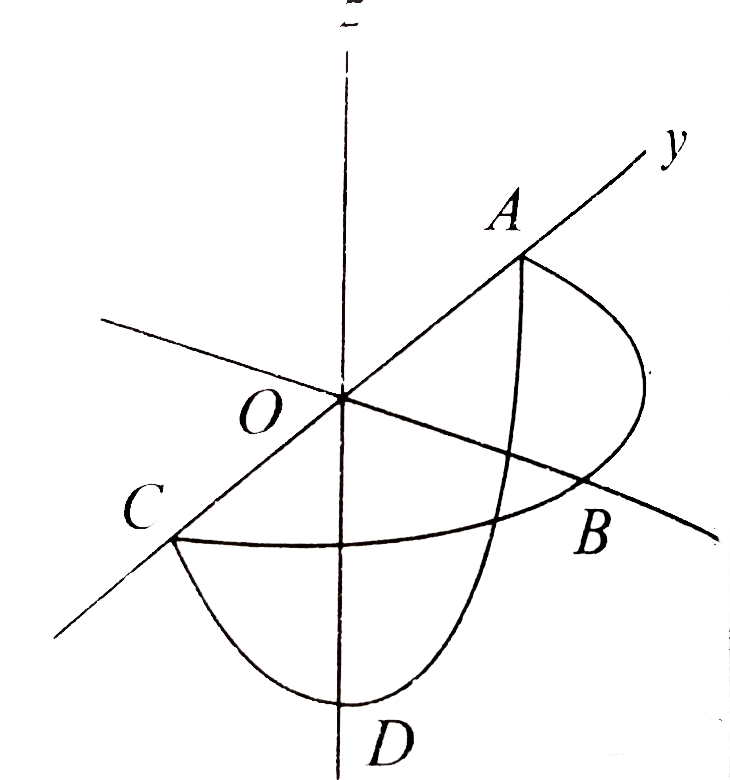
If →B be directed along the +z axis and increases at the rate of 10−2Teslasecond. the magnitude and sense of the induced emf in the loop as seen along the field direction will beAzeroB5π4√2 mV in the counterclockwise senseC5π4√2 mV in the clockwise senseD5π2√2mV in the clockwise sense.In Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is
 Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)

The number of atoms lying in the same plane for the anionic part of compound B are
View SolutionFind the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R
View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
View SolutionA current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-y plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
View SolutionA current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common centre is
View Solution
