A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-y plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
μ0i2√2R
μ0i2R
μ0i4R
μ0i√2R
The correct Answer is:A
To solve the problem of finding the resultant magnetic field at the common center of two identical semicircular current loops, we will follow these steps:
Step 1: Understanding the Configuration
We have two semicircular loops, each of radius R. One loop lies in the x-y plane, and the other lies in the x-z plane. The current i flows through both loops.
Step 2: Determine the Magnetic Field due to Each Semicircular Loop
Using the formula for the magnetic field at the center of a semicircular loop of radius R carrying a current i:
B=μ0i4R
where μ0 is the permeability of free space.
Step 3: Calculate the Magnetic Field Direction
1. For the semicircular loop in the x-y plane (B1):
- By the right-hand rule, if the current flows counterclockwise when viewed from above, the magnetic field B1 will point in the positive z-direction.
- Therefore, B1=μ0i4R^k.
2. For the semicircular loop in the x-z plane (B2):
- Again, using the right-hand rule, if the current flows counterclockwise when viewed from the positive y-axis, the magnetic field B2 will point in the negative y-direction.
- Therefore, B2=−μ0i4R^j.
Step 4: Resultant Magnetic Field Calculation
The resultant magnetic field Bnet at the common center is the vector sum of B1 and B2:
Bnet=B1+B2=μ0i4R^k−μ0i4R^j
Step 5: Final Result
Thus, the resultant magnetic field at the common center due to the two semicircular parts is:
Bnet=μ0i4R^k−μ0i4R^j
We have two semicircular loops, each of radius R. One loop lies in the x-y plane, and the other lies in the x-z plane. The current i flows through both loops.
Using the formula for the magnetic field at the center of a semicircular loop of radius R carrying a current i:
B=μ0i4R
where μ0 is the permeability of free space.
1. For the semicircular loop in the x-y plane (B1):
- By the right-hand rule, if the current flows counterclockwise when viewed from above, the magnetic field B1 will point in the positive z-direction.
- Therefore, B1=μ0i4R^k.
- Again, using the right-hand rule, if the current flows counterclockwise when viewed from the positive y-axis, the magnetic field B2 will point in the negative y-direction.
- Therefore, B2=−μ0i4R^j.
The resultant magnetic field Bnet at the common center is the vector sum of B1 and B2:
Bnet=B1+B2=μ0i4R^k−μ0i4R^j
Thus, the resultant magnetic field at the common center due to the two semicircular parts is:
Bnet=μ0i4R^k−μ0i4R^j
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)
1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)
1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions
2 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions
1 Video
Similar Questions
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude to →B at the origin.
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
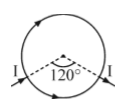
View Solution
Knowledge Check
A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common centre is
Aμ0i2√2RBμ0i2RCμ0i4RDμ0i√2RA 4 A current carrying loop consists of three identical quarter circles of radius 5 cm lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin joined together, value of B at the origin is
Aμ010(ˆi+ˆj−ˆk)TBμ010(−ˆi+ˆj+ˆk)TCμ05(ˆi+ˆj+ˆk)TD10μ0(ˆi+ˆj+ˆk)TIn Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is
 Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
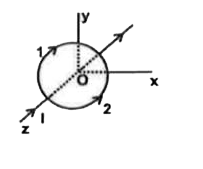
A current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is
View SolutionTwo similar coils of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and 2I, respectively. The resultant magnetic field induction at the centre will be
View SolutionTwo similar circular loops of radius R are lying concentrically with their planes at right angles to each other. The currents flowign in them are l and l√3 respectively. The magnetic field at the centre of the coil is
View SolutionA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
View SolutionA current of 10A is passing through a long wire which has semicircular loop of the radius 20cm as shown in the figure. Magnetic field produced at the centre of the loop is

View Solution