An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
![An infinite cylindrical wire of radius R and having current density varying with its radius r as, J = J(0)[1-(r//R)]. Then answer the following questions. Magnitude of maximum magnetic field is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_MCA_E01_139_Q01.png)
Magnitude of maximum magnetic field is
J0R6μ0
316J0Rμ0
516J0Rμ0
56J0Rμ0
The correct Answer is:B
Current with in radius r:I=∫rJdA
⇒I=∫r0J0[1−RR]2πrdr=2πj0[r22−r33R]
Apply ampere's law B2πr=μ0I
B2πr=μ02πJ0(r22−r33R)⇒B=μ0J0[r2−r23R]
to find max B: dBdr=0⇒r=3R/4
Bmax=μ0J90[3R/42−(3R/4)23r]=3R16μ0J0.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Multiple Correct
Explore 34 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- Moving charges and magnetismBook:CENGAGE PHYSICSChapter:Moving charges and magnetismExercise:Question Bank
Explore 20 Videos
Similar Questions
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View Solution
Knowledge Check
An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Position where magnetic field strength is maximum.ARB3R/4Cr/2DR/4An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Graph between the magnetic field and radius isA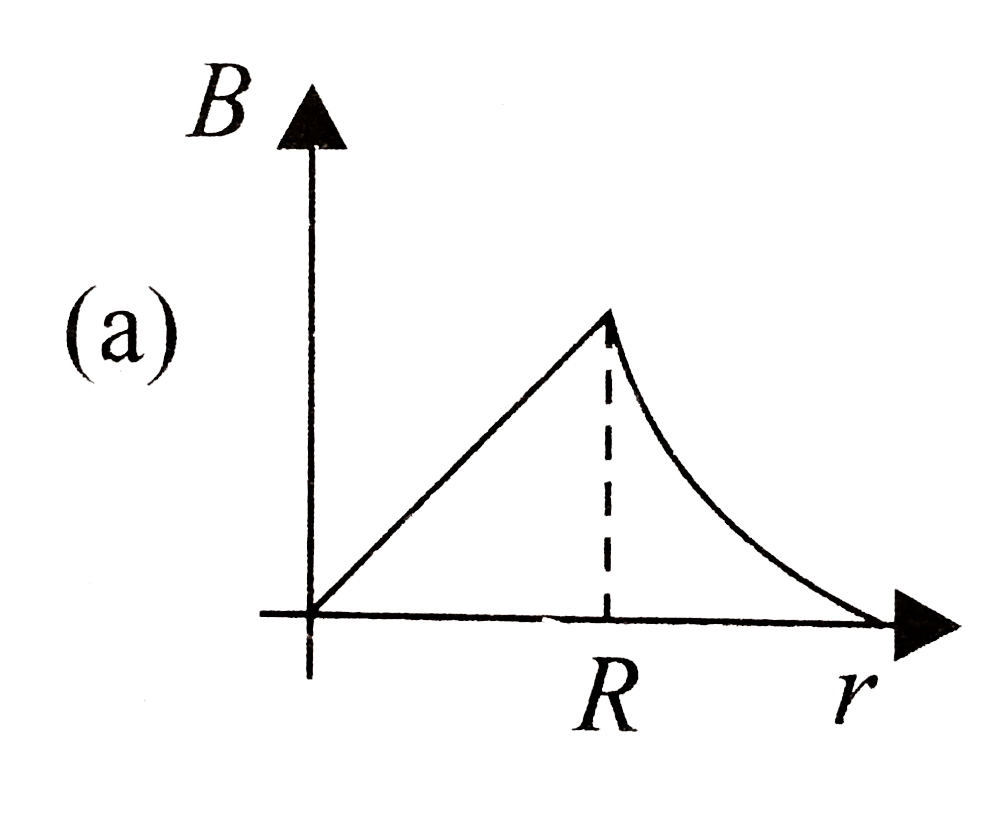 B
B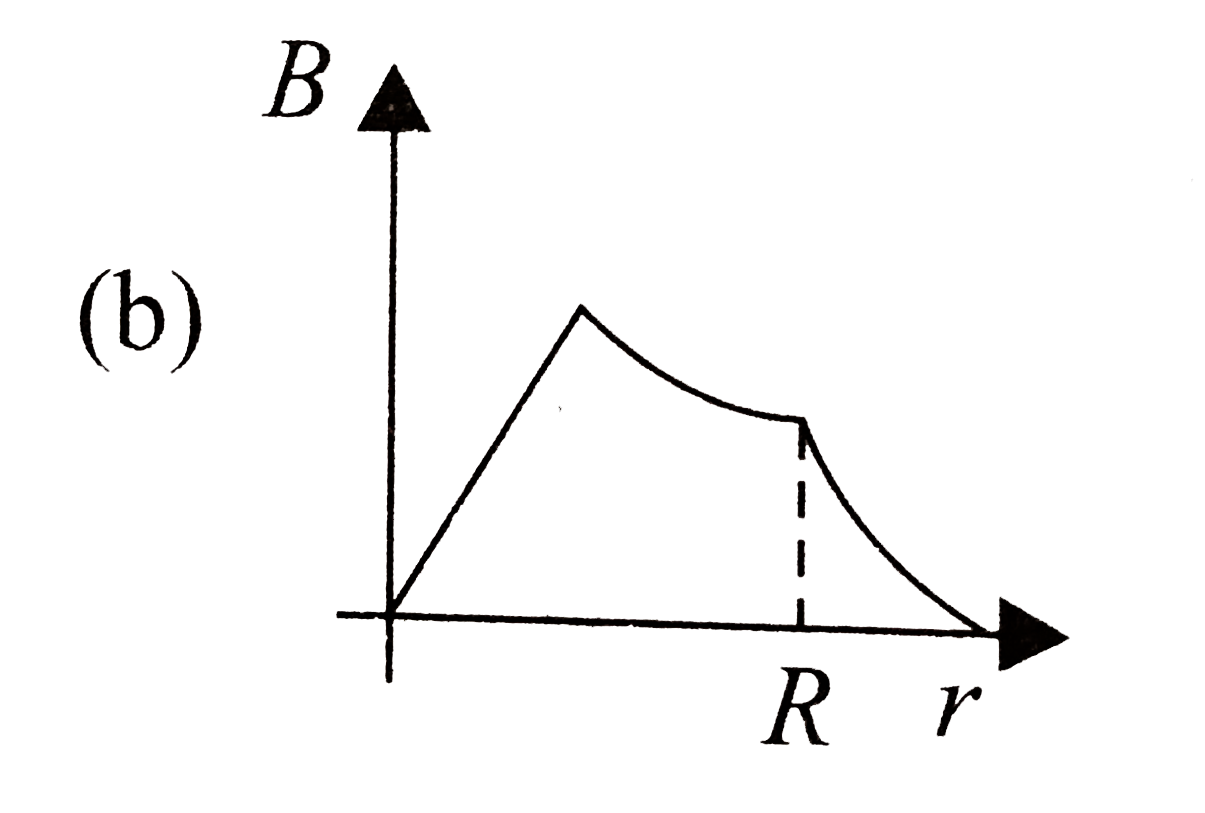 C
C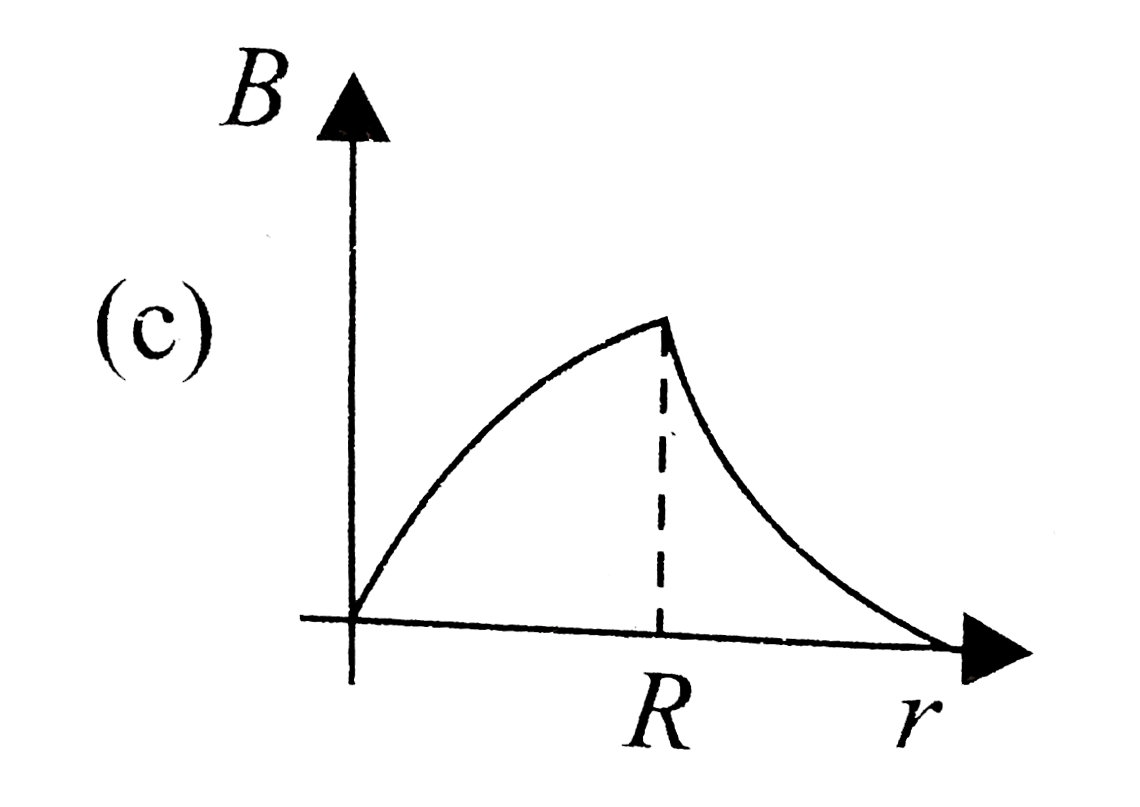 D
D
A cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
AπJ0R22B2πJ0R23C4πJ0R23Dnone of these
A non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View SolutionAn infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
View SolutionA long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r1(r1<R) is
View Solution

