A conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
(a) The emf will be maximum at the moment when flux is zero
(b) The emf will be 0 at the moment when flux ismaximum
( c) The emf will be maximum at the moment when plane of the loop is parallel to the magnetic field
(d) The phase difference between the flux and the emf π/2
The correct Answer is:A, B, C, D
(a,b,c,d): ϕ=Bacosθ,θ=ωt
e=−dϕdt=Baωsinθ
at θ=π2,ϕ=0 and e is maximum. At θ=0,ϕ is maximum and e is zero. Emf is maximum where θ=π2 and for this plane of loop is parallel to magnetic field. Clearly phase difference between flux and emf is π/2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension
36 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
Knowledge Check
When a 'J' shaped conducting rod rotating in its own plane with constant angular velocity omega, avout one of its end P, in a uniform magnetic field →B directed normally into the plane of paper) then magnetic of emf induced across it will be
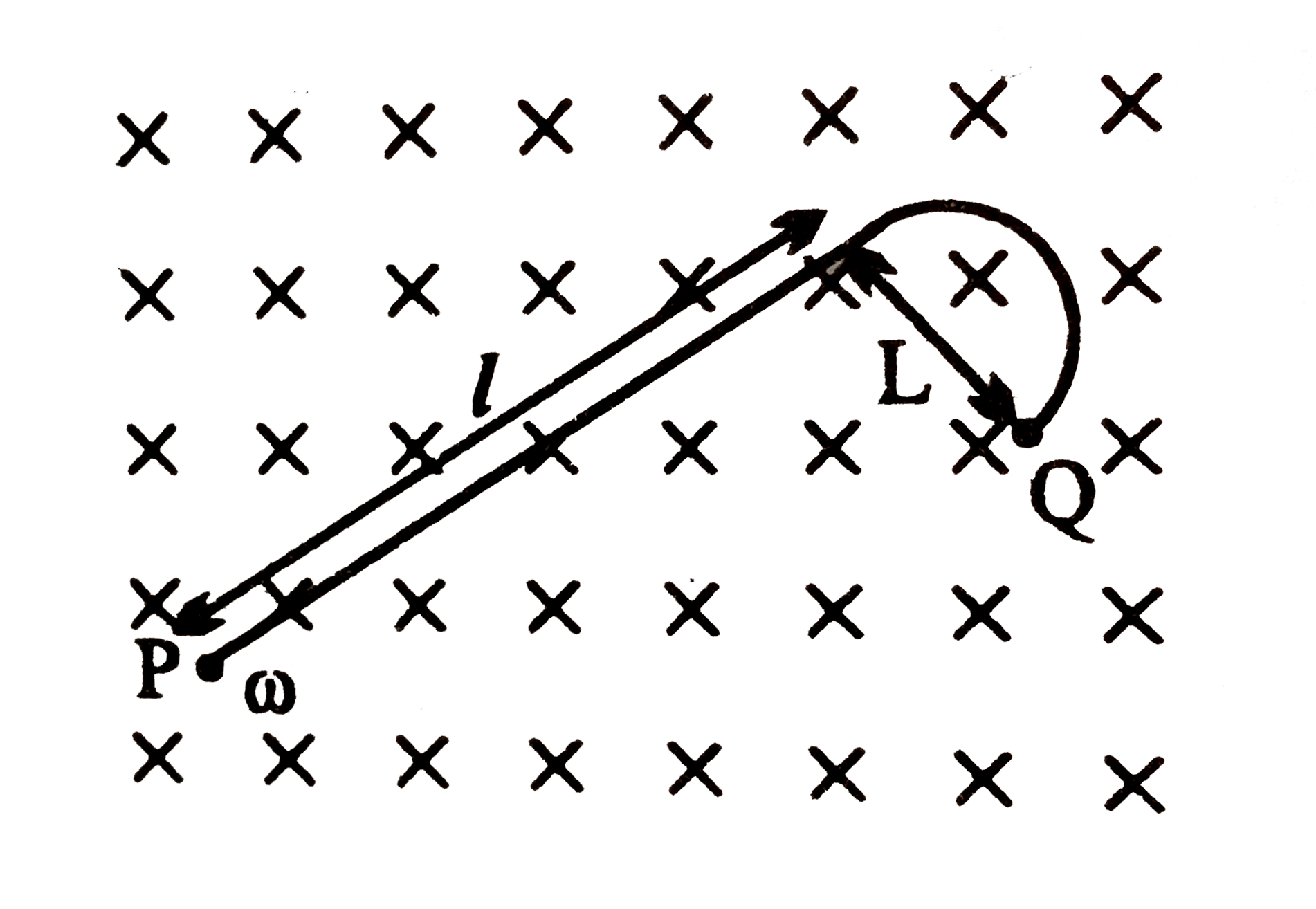 ABω√L2+l2B12BωL2C1Bω(L2+l2)D12Bωl2
ABω√L2+l2B12BωL2C1Bω(L2+l2)D12Bωl2When a 'j' shaped conducting rod is rotating in its own plane with constant angular velocity ω about one of its ends P in a uniform magnetic field →B ( directed normally into the plane of paper ) the magnitude of emf induced across it will be
 ABω√L2+l2B12BωlL2C12Bω(L2+l2)D12Bωl2
ABω√L2+l2B12BωlL2C12Bω(L2+l2)D12Bωl2A conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
 ABωl2B12Bωl2C18Bωl2Dzero
ABωl2B12Bωl2C18Bωl2Dzero
A conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA circular conducting ring is rotated about one its diameter in a magnetic field
View SolutionA conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
View Solution
