A charge q coulomb moves in a circle at n revolution per second and the radius of the circle is r metre. Then magnetic feild at the centre of the circle is
The correct Answer is:C
To solve the problem of finding the magnetic field at the center of a circular path along which a charge q is moving, we can follow these steps:
1. Identify the Given Parameters:
- Charge q (in coulombs)
- Frequency n (in revolutions per second)
- Radius r (in meters)
2. Determine the Current I:
- The charge q completes n revolutions in one second. Therefore, the total charge passing through a point in one second (which is the definition of current) can be calculated as:
I=qT
- Here, T (the time period for one revolution) is given by:
T=1n seconds
- Substituting T into the current equation gives:
I=q⋅n
3. Use the Formula for Magnetic Field at the Center of a Circular Loop:
- The magnetic field B at the center of a circular loop carrying current I is given by:
B=μ0I2r
- Here, μ0 is the permeability of free space.
4. Substitute the Current I into the Magnetic Field Formula:
- Now, substituting I=qn into the magnetic field formula:
B=μ0(qn)2r
5. Final Expression for the Magnetic Field:
- Therefore, the magnetic field at the center of the circle is:
B=μ0qn2r
6. Direction of the Magnetic Field:
- According to the right-hand rule, the direction of the magnetic field at the center of the circle is out of the plane of the circle (towards the observer).
Final Answer:
The magnetic field at the center of the circle is given by:
B=μ0qn2r
with the direction being out of the screen.
---
- Charge q (in coulombs)
- Frequency n (in revolutions per second)
- Radius r (in meters)
- The charge q completes n revolutions in one second. Therefore, the total charge passing through a point in one second (which is the definition of current) can be calculated as:
I=qT
- Here, T (the time period for one revolution) is given by:
T=1n seconds
- Substituting T into the current equation gives:
I=q⋅n
- The magnetic field B at the center of a circular loop carrying current I is given by:
B=μ0I2r
- Here, μ0 is the permeability of free space.
- Now, substituting I=qn into the magnetic field formula:
B=μ0(qn)2r
- Therefore, the magnetic field at the center of the circle is:
B=μ0qn2r
- According to the right-hand rule, the direction of the magnetic field at the center of the circle is out of the plane of the circle (towards the observer).
The magnetic field at the center of the circle is given by:
B=μ0qn2r
with the direction being out of the screen.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
An electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View SolutionA particle moving in uniform circle makes 18 revolutions in 1 minutes. If the radius of the circle is 10 cm, the speed of the particle is
View Solution
Knowledge Check
An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is
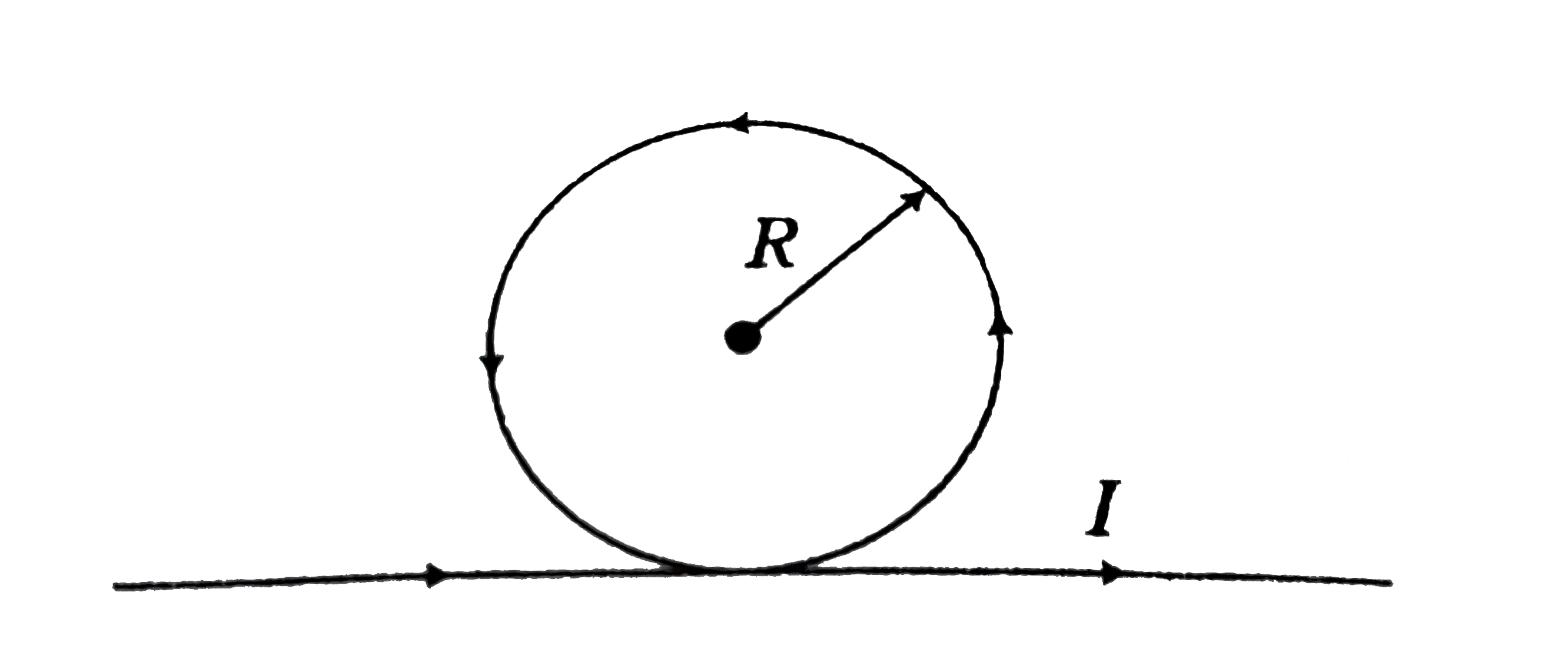 Aμ02I4πR(π+1)Bμ02I4πR(π−1)Cμ0I8πR(π+1)Dzero
Aμ02I4πR(π+1)Bμ02I4πR(π−1)Cμ0I8πR(π+1)DzeroA charge of 10−6C is describing a circular path of radius 1cm making 5 revolution per second. The magnetic induction field at the centre of the circle is
Aπ×10−10TBπ×10−9TCπ2×10−10TDπ2×10−9TIn total, 10 charges (5 of them are +q each and other 5 are −q each) are placed randomly on the circumference of a circle. The radius of the circle is R. The electric potential at the center of this circle due to these charges will be
A0B10Kq/RC5Kq/RDCannot be calculated unless the positions of the charges on the circle are specified.
A charge 'e' moves round a circle of radius 'r' with a uniform speed 'v'. The magnitude of the magnetic induction at the centre of the circle is
View SolutionA helium nucleus makes a full rotation in a circle of radius 0.8 metre in two seconds. The value of the magnetic field B at the centre of the circle will be
View SolutionA circle touches the x-axis and also touches the circle with centre (0,3) and radius 2. The locus of the centre of the circle is :
View SolutionA circle touches the x-axis and also touches the circle with centre (0,3) and radius 2. The locus of the centre of the circle is
View SolutionA helium nucleus makes full rotation in a circle of radius 0.8 m in 2.5 seconds. The value of magnetic field B at the centre of the circle will be
View Solution
