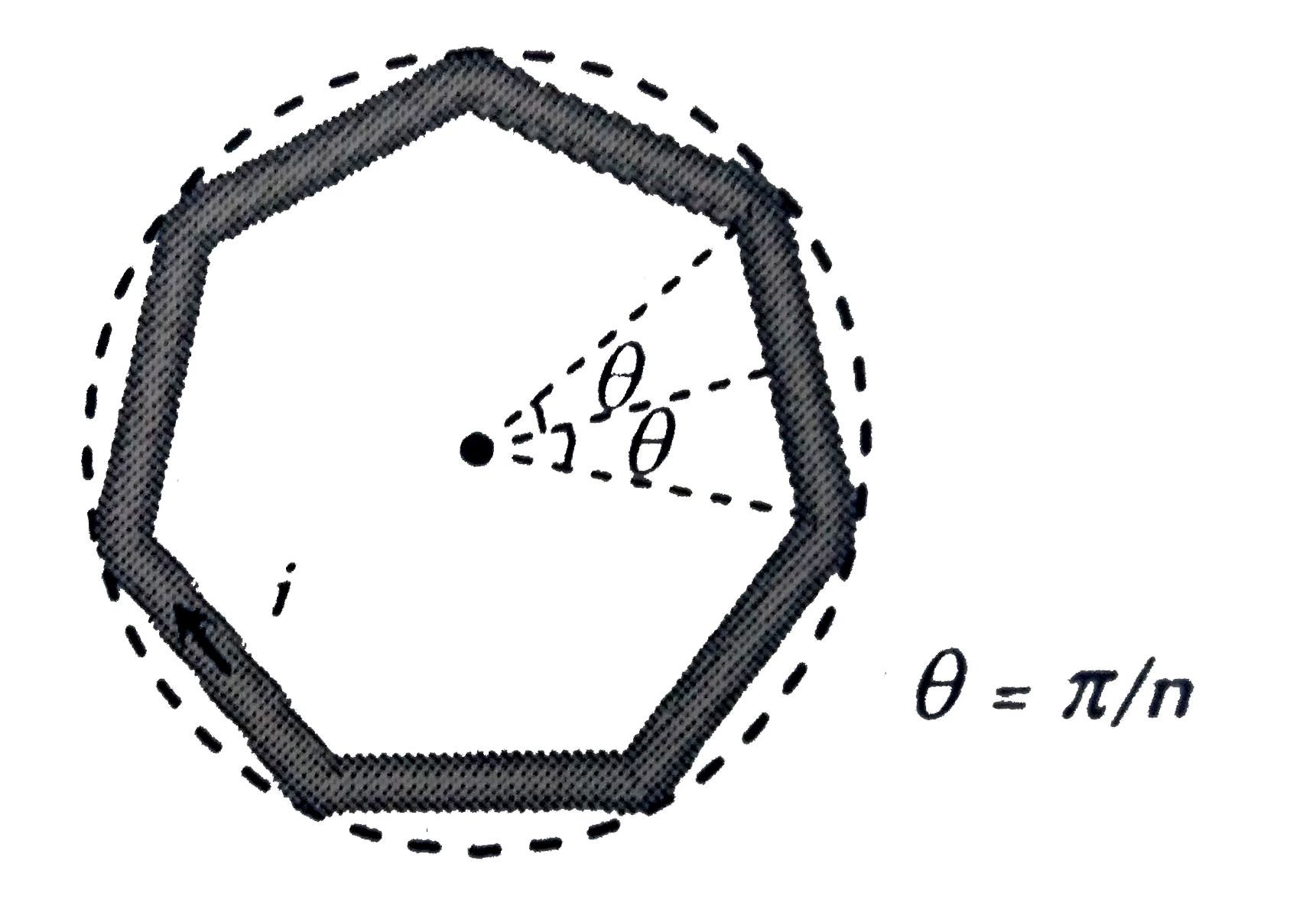
A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is

A

$\frac{μ_{0} I}{π R} (\frac{tan π}{n})$

B

$\frac{μ_{0} I}{4 π R} \frac{tan π}{n}$

C

$\frac{μ_{0} I}{2 π R} (\frac{tan π}{n})$

D

$\frac{μ_{0} I}{2 π R} (\frac{cos π}{n})$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To find the magnetic field induction at the center of a regular polygon with $n$ sides, inscribed in a circle of radius $R$ , due to one side of the polygon, we can follow these steps:
1. Identify the Geometry:
- A regular polygon with $n$ sides is inscribed in a circle of radius $R$ . The center of the polygon coincides with the center of the circle.
2. Calculate the Angle Subtended by One Side:
- The total angle around a point is $360^{\circ}$ or $2 π$ radians. Therefore, the angle subtended by one side of the polygon at the center is:
$θ = \frac{2 π}{n}$
3. Determine the Perpendicular Distance:
- When we bisect the angle $θ$ , we get two angles of $\frac{θ}{2} = \frac{π}{n}$ . The perpendicular distance $D$ from the center to the midpoint of one side is given by:
$D = R cos (\frac{π}{n})$
4. Use the Formula for Magnetic Field due to a Finite Wire:
- The magnetic field $B$ at a distance $D$ from a straight wire carrying current $I$ is given by:
$B = \frac{μ_{0} I}{4 π D} (sin θ_{1} + sin θ_{2})$
- Here, $θ_{1}$ and $θ_{2}$ are the angles from the wire to the endpoints of the segment, which in this case are both $\frac{π}{n}$ .
5. Substitute Values:
- Since $sin θ_{1} = sin θ_{2} = sin (\frac{π}{n})$ , we have:
$B = \frac{μ_{0} I}{4 π D} (2 sin (\frac{π}{n}))$
- Substituting $D = R cos (\frac{π}{n})$ :
$B = \frac{μ_{0} I}{4 π R cos (\frac{π}{n})} (2 sin (\frac{π}{n}))$
6. Simplify the Expression:
- This simplifies to:
$B = \frac{μ_{0} I}{2 π R} \cdot \frac{sin (\frac{π}{n})}{cos (\frac{π}{n})}$
- Which can be expressed as:
$B = \frac{μ_{0} I}{2 π R} tan (\frac{π}{n})$
7. Direction of the Magnetic Field:
- Using the right-hand thumb rule, the direction of the magnetic field due to the current flowing in the wire will be inside the plane of the polygon.
Final Result:
The magnetic field induction at the center of the polygon due to one side is:
$B = \frac{μ_{0} I}{2 π R} tan (\frac{π}{n})$

Updated on:7/8/2024

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$ . Net magnetic field at centre will be

A $\frac{μ_{0} i}{2 π a} tan \frac{π}{n}$
B $\frac{μ_{0} n i}{2 π a} tan \frac{π}{n}$
C $\frac{2}{π} \frac{n i}{a} μ_{0} tan \frac{π}{n}$
D $\frac{n i}{2 a} μ_{0} tan \frac{π}{n}$
A current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when $n \to \infty$ is (R is the radius of its circumcircle)
A $\frac{μ_{0} n i}{2 π R} tan \frac{π}{6}$
B $\frac{μ_{0} n i}{2 π R} tan \frac{π}{R}$
C $\frac{μ_{0} i}{2 R}$
Dzero
A loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex, then the magnitude of the magnetic induction vector $\to B$ at the centre of the loop is –
A $n \frac{μ_{0} I}{2 π R} tan . \frac{π}{n}$
B $\frac{μ_{0} I}{2 R}$
C $n \frac{μ_{0} I}{2 π R} tan . \frac{2 π}{n}$
D $\frac{μ_{0} I}{π R} tan . \frac{π}{n}$

CENGAGE PHYSICS-SOURCES OF MAGNETIC FIELD-Exercise (single Correct )

Home
Ask Doubt
Profile