Figure shows three cases: in all case the circular part has radius r and straight ones are infinitely long. For the same current the ratio of field B at centre P in the three case B1:B2:B3 is
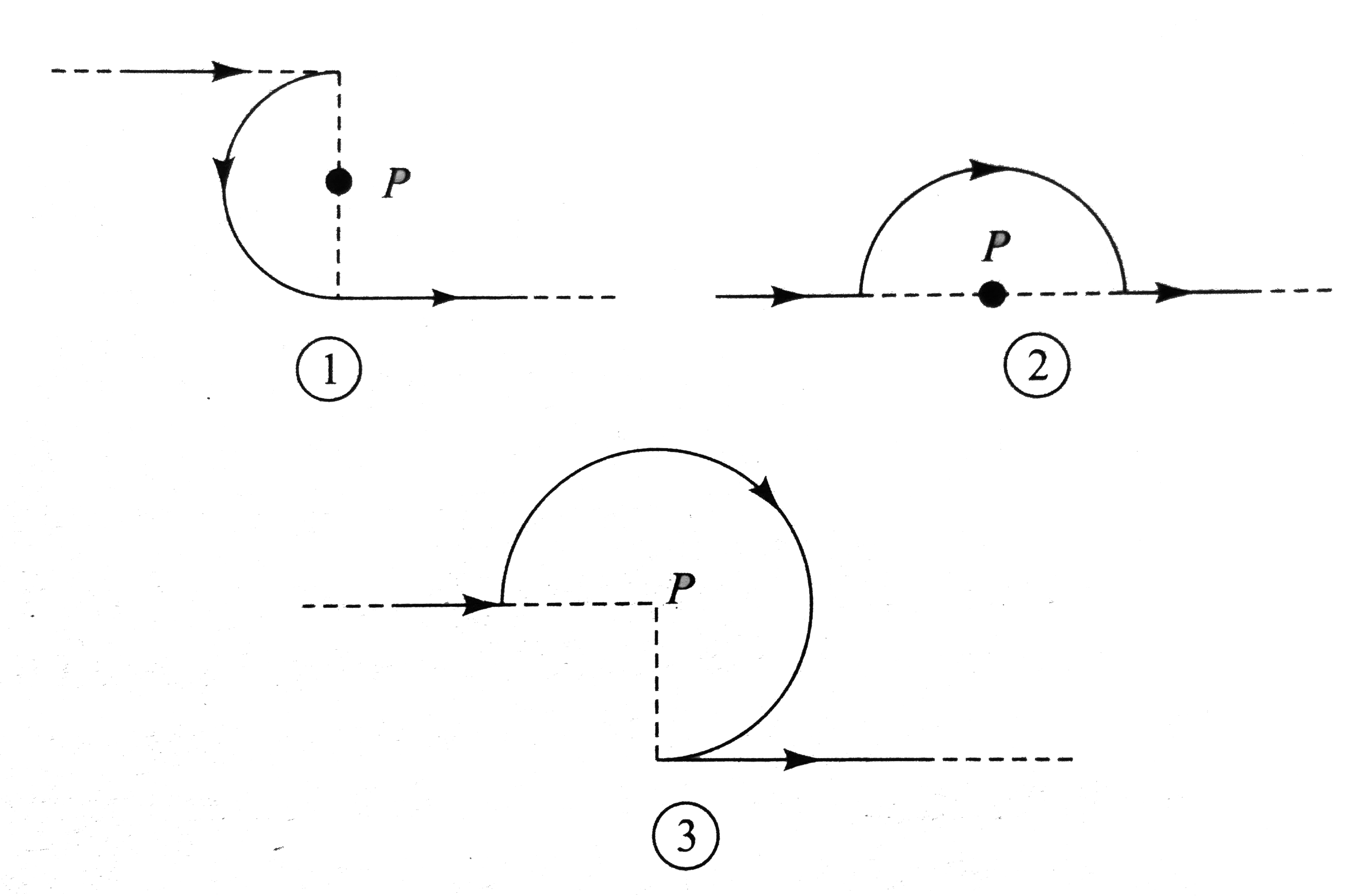
(−π2):(π2):(3π4−12)
(−π2+1):(π2+1):(3π4+12)
(−π2):(π2):(3π4)
(−π2−1):(π2−14):(3π4+12)
The correct Answer is:A
(a) →B1=μ0I4r⊙,→B2=μ0I4r⊗
→B3=μ0I2r(34)⊗+μ0I4πr⊙=μ0I4r[32⊗+1π⊙]
=μ0I4r[3π−22π]⊗=μ0I4r(2π)(3π4−12)⊗
B1:B2:B3=−(π2):(π2):(3π4−12)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
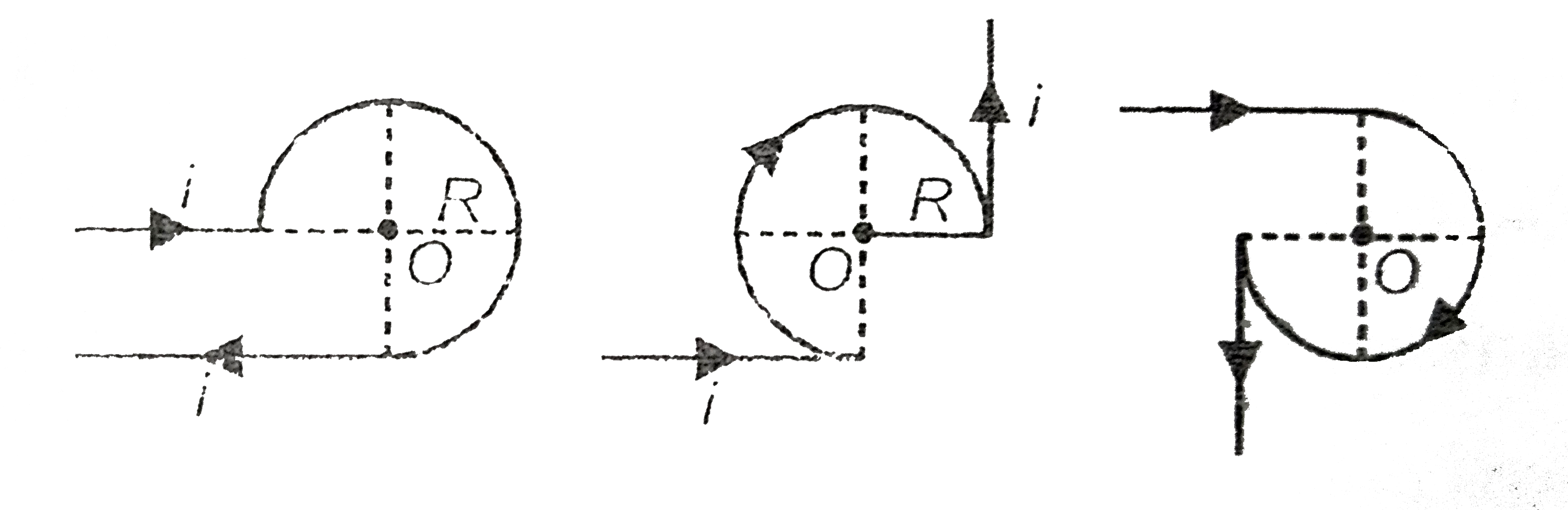
The figure shows three long straight current carrying conductors. The straight parts are long and the circular part in each case in (34)th of a complete circle, Let Ba,BbandBc represents the strength of field at the centre O in the three cases, then
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 21is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View Solution
Knowledge Check
The magnetic field at the centre of a circular coil of radius r is π time that due to a long straight wire at a distance r from it for equal currents. The following figure show three cases. In all cases the circular part has radius r and straight ones are infinitely long. For same current, the B field at the centre P in cases 1, 2, 3, has the ratio
 A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C−π2:π2:3π4D(−π2−1):(π1−14):(3π4+12)
A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C−π2:π2:3π4D(−π2−1):(π1−14):(3π4+12)(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
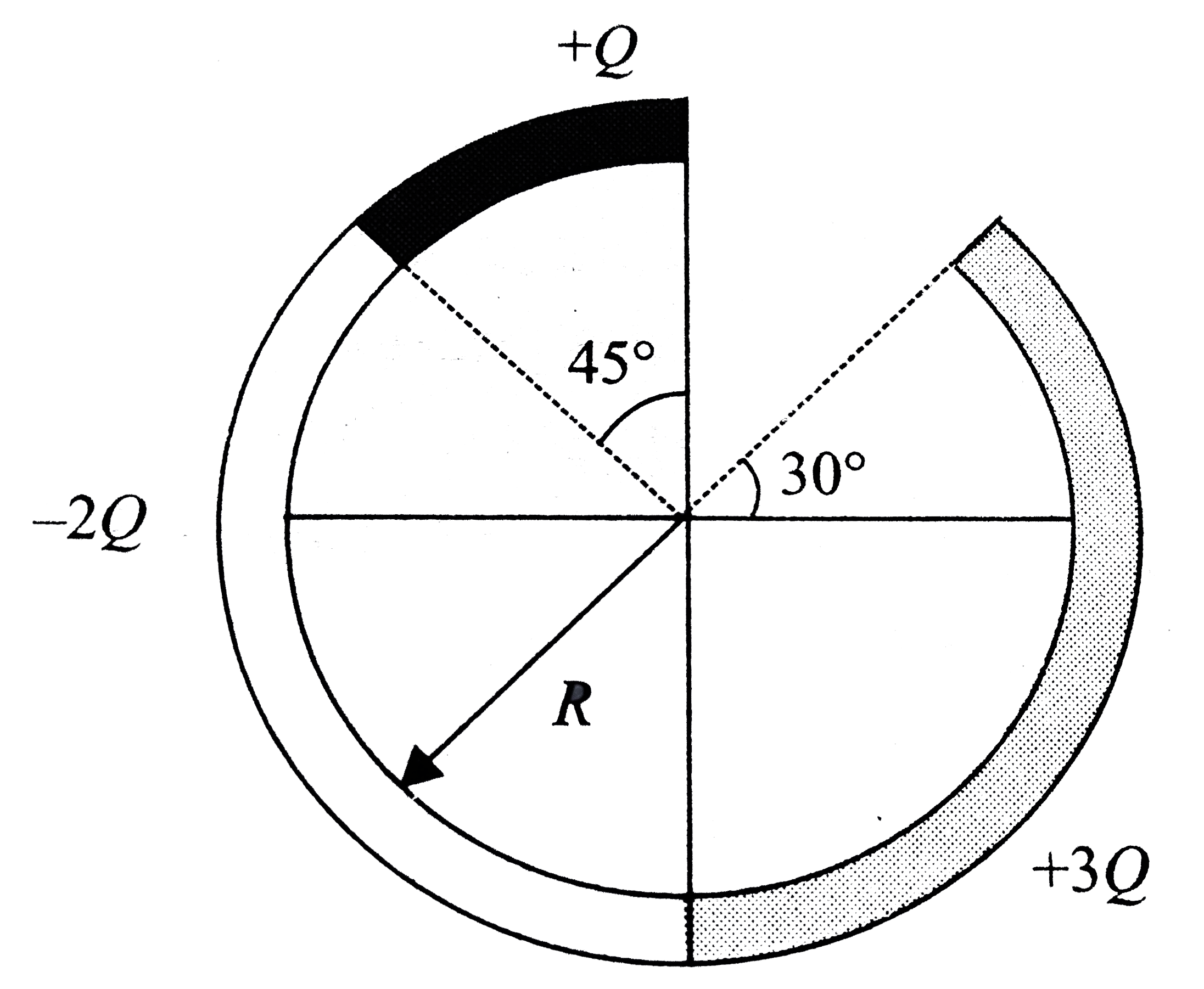 .AQ2πε0RB5Q12πε0RC3Q32πε0RDnone of these
.AQ2πε0RB5Q12πε0RC3Q32πε0RDnone of theseA circular coil A has a radius R and current flowing through it is I. Another circular coil B has a radius 2R and if 2I is the current flowing throgh it, then the magneitc field at the centre of the circular coil are in the ratio (i.e, BA to BB) of
A4:1B2:1C3:1D1:1
A circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 21is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA long wire is first bent into a circular coil of one turn and then into a circular coil of smaller radius, having n identical turns. If the same current passes in both the cases, find the ratio of the magnetric fields produced at the centre in the two cases.
View SolutionA conductor has three segments, two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?

View Solution

