A current of 1/(4π) ampere is flowing in a long straight conductor. The line integral of magnetic induction around a closed path enclosing the current carrying conductor is
10−7Wbm−1
4π−7Wbm−1
16π2×10−7Wbm−1
zero.
The correct Answer is:A
To solve the problem, we will use Ampere's Circuital Law, which relates the magnetic field around a closed loop to the current passing through the loop. The law states that the line integral of the magnetic field B around a closed path is equal to μ0 times the current I enclosed by that path.
1. Identify the Given Values:
- Current I=14π A
- Permeability of free space μ0=4π×10−7T m/A
2. Apply Ampere's Circuital Law:
- According to Ampere's Circuital Law:
∮B⋅dl=μ0Ienc
- Here, Ienc is the current enclosed by the closed path.
3. Substitute the Values:
- Substitute μ0 and I into the equation:
∮B⋅dl=(4π×10−7)(14π)
4. Simplify the Expression:
- The 4π terms cancel out:
∮B⋅dl=10−7T m
5. Final Result:
- The line integral of magnetic induction around the closed path is:
∮B⋅dl=10−7T m
- Current I=14π A
- Permeability of free space μ0=4π×10−7T m/A
- According to Ampere's Circuital Law:
∮B⋅dl=μ0Ienc
- Here, Ienc is the current enclosed by the closed path.
- Substitute μ0 and I into the equation:
∮B⋅dl=(4π×10−7)(14π)
- The 4π terms cancel out:
∮B⋅dl=10−7T m
- The line integral of magnetic induction around the closed path is:
∮B⋅dl=10−7T m
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
Magnetic induction at point P from shown current-carrying long conductors is given by-
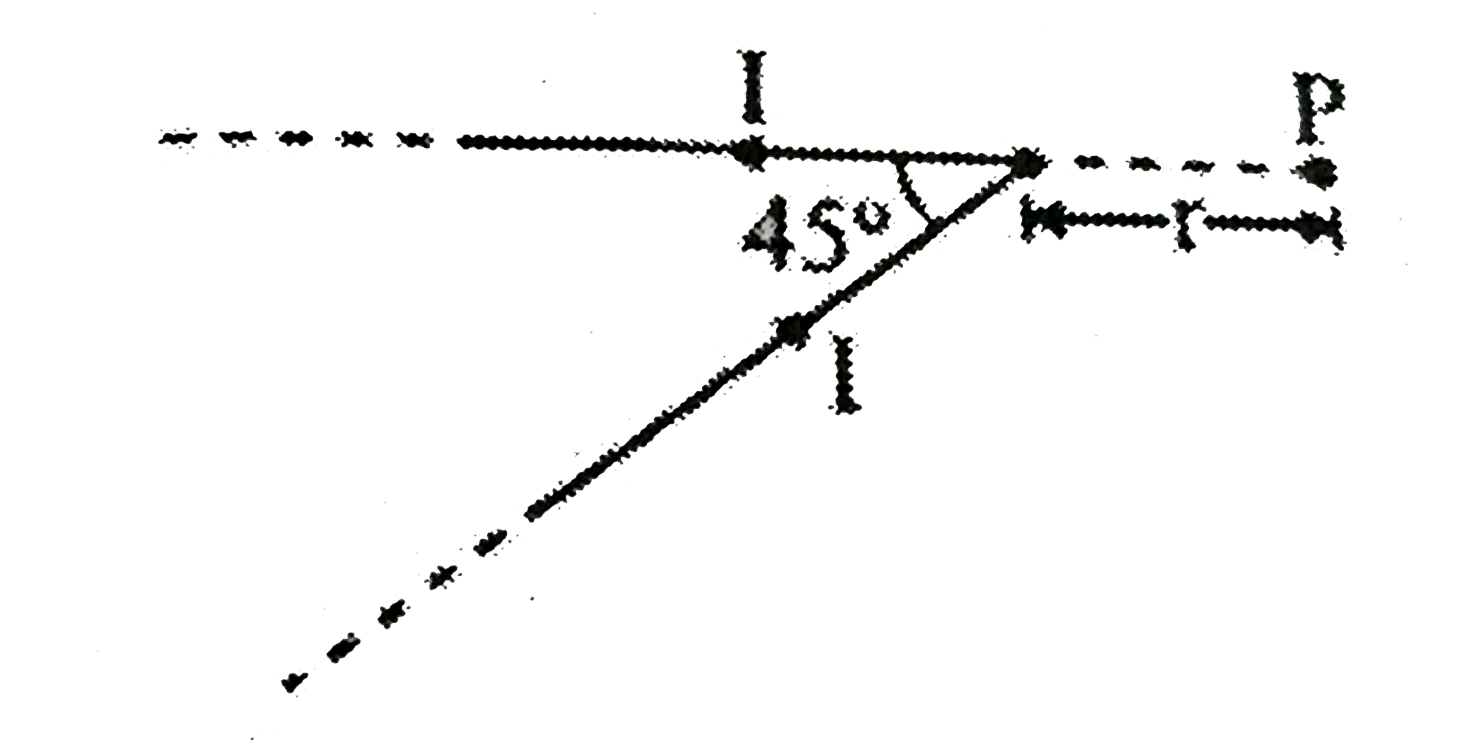 A5μ0I2√2πr(√2−1)Bμ0I√2πr(√2−1)C8μ0I2πr(√2−1)Dμ0I4πr(√2−1)
A5μ0I2√2πr(√2−1)Bμ0I√2πr(√2−1)C8μ0I2πr(√2−1)Dμ0I4πr(√2−1)Magnetic field at a point on the line of current carrying conductor is
AmaximumBinfinityCzeroDfinite valueThe magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distance
Magnetic Force On A Current Carrying Conductor
View SolutionWhat is the shape of magnetic field lines due to a straight current - carrying conductor ?
View SolutionWhat is the shape of the magnetic field lines due to a straight current carrying conductor ?
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View Solution
