A straight wire lies along a body diagonal of an imaginary cube of side $a = 20 c m,$ and carries a current of 5 A (as shown in Fig. 1.61). Find the force on it due to a uniform field $\to B = 0.6 ˆ j T .$

Video Solution

Text Solution

Verified by Experts

In order to use equation $\to F = i \to l \times \to B$ , we would need to find the
angle between $\to l and \to B$ . We avoid this task by using unit vector
notation. Form the problem figure, we see that
$\to l = a ˆ i - a ˆ j + a ˆ k$
Thus, the force is $\to F = I \to l \times \to B = I a B (ˆ i - ˆ j + ˆ k) \times (ˆ j)$
$= I a B (- ˆ i + ˆ k)$
The force lies in the xz plane and has a magnitude
$F = \sqrt{2} I a B = 0.85 N$

Updated on:21/07/2023

The magnetic force per unit length on a wire carrying a current of 10 A and making an angle of $45^{\circ}$ with the direction of a uniform magnetic field of 0.20 T is
A $2 \sqrt{2} N m^{- 1}$
B $\frac{2}{\sqrt{2}} N m^{- 1}$
C $\frac{\sqrt{2}}{2} N m^{- 1}$
D $4 \sqrt{2} N m^{- 1}$
The rigid conducting thin wire frame carries an electric current I and this frame is inside a uniform magnetic field $\to B$ as shown in Fig. 1.146. Then,

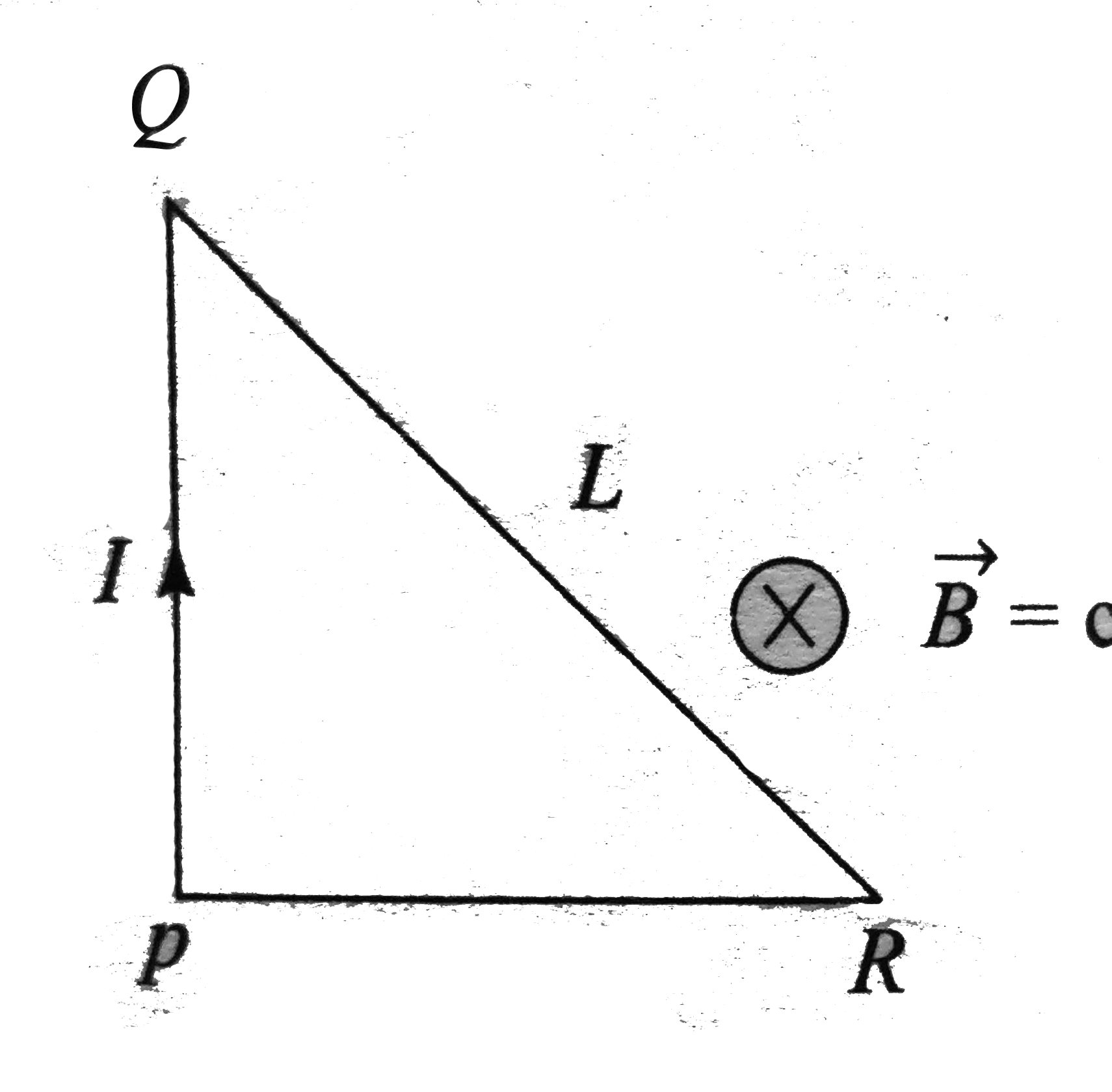AThe net magnetic force on the frame is zero but the torque is not zero
BThe net magnetic force on the frame and the torque due to magnetic field are both zero.
Cthe net magnetic force on the frame is not zero and the torque is also not zero.
DNone of these
The magnetic force per unit length on a wire carrying a current of 10 A and making an angle of $45^{\circ}$ with the direction of a uniform magnetic field of 0.20 T is
A $2 \sqrt{2} N m^{- 1}$
B $\frac{2}{\sqrt{2}} N m^{- 1}$
C $\frac{\sqrt{2}}{2} N m^{- 1}$
D $4 \sqrt{2} N m^{- 1}$