Shows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

(a) The force on the wire due to the magnetic field is
→F=i→l×→BorF=ilb
It acts towards right in the figure provided. If the wire does not
slide on the rails, the force of friction by the rails should be
equal to F. If μ0 be the minimum coefficient of friction which
can prevent sliding, this force is equal to μ0mg. Thus,
μ0mg=ilBorμ0=ilBmg
(b) If the friction coefficient is μ=μ02=ilB2ng, the wire will
slide towards right. The frictional force by the rails is f=μmg=ilB2→wards≤ft
The resultant force is ilB−ilB2=ilB2 towards right. The
accleration will be a=ilB2m. The wire will slide towards
right with this acceleration.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise1.3
14 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A circular coil with area A and N turns is free to rotate about a diameter that coincides with the x-axis. Current I is circulating in the coil. There is a uniform magnetic field →B in the the positive y direction. Calculate the magnitude and direction of the torque →τ and the value of the potential energy U, when the coil is oriented as shown in parts (a) through (d) of Fig. 1.79.




View SolutionAn α−particle is describing a circle of radius 0.45 m in a field of magnetic induction of 1.2 T. Find its speed, frequency of rotation and kinetic energy. What potential difference will be required to accelerate the particle so as to give this much of the energy to it? The mass of α−particle is 6.8×10−27kg and its charge is twice the charge of proton, i.e.,3.2×10−19C.
View SolutionA charged particle of mass 5 mg and charge q=+2μC has velocity →v=2ˆi−3ˆj+4ˆk. Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field →B=3ˆj−2ˆk.→vand→B are in ms−1andWbm−2 , respectively.
View SolutionAir is filled at 60 ∘ C in a vessel of open mouth. The vessel is heated to a temperature T so that 14 part of air escapes. The value of T(in 0C) is
View SolutionA closely wound solenoid of 3000 turns and area of cross-section 2×10−4m2, carrying a current of 6A, is suspended through its center allowing it to turn in a horizontal plane. The magnetic moment (in (J)(T)−1 ) associated with the solenoid is
View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is mu . (a) What should be the minimum value of mu which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of mu is half the value found in the previous part.
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA metal wire PQ of mass 10g lies at rest on two horizontal metal rails separated by 5cm as shown in Fig. A vertically downward magnetic field of magnitude 0.80T exist in the space. The resistance of the circuit is slowly decreased and it is found that when the resistance goes below 20.0Omega the wire PQ starts sliding on the rails. The coefficient of friction between wires and rails is found. The coefficient of friction between wires and rails is found to be n//25 . find n
View SolutionA metal wire of mass m slides without friction on two horizontal rails spaced distance d-apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upwards, and a battery is sending a current I through them. Find the velocity of the wire as a function of time, assuming it to be at rest initially.
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
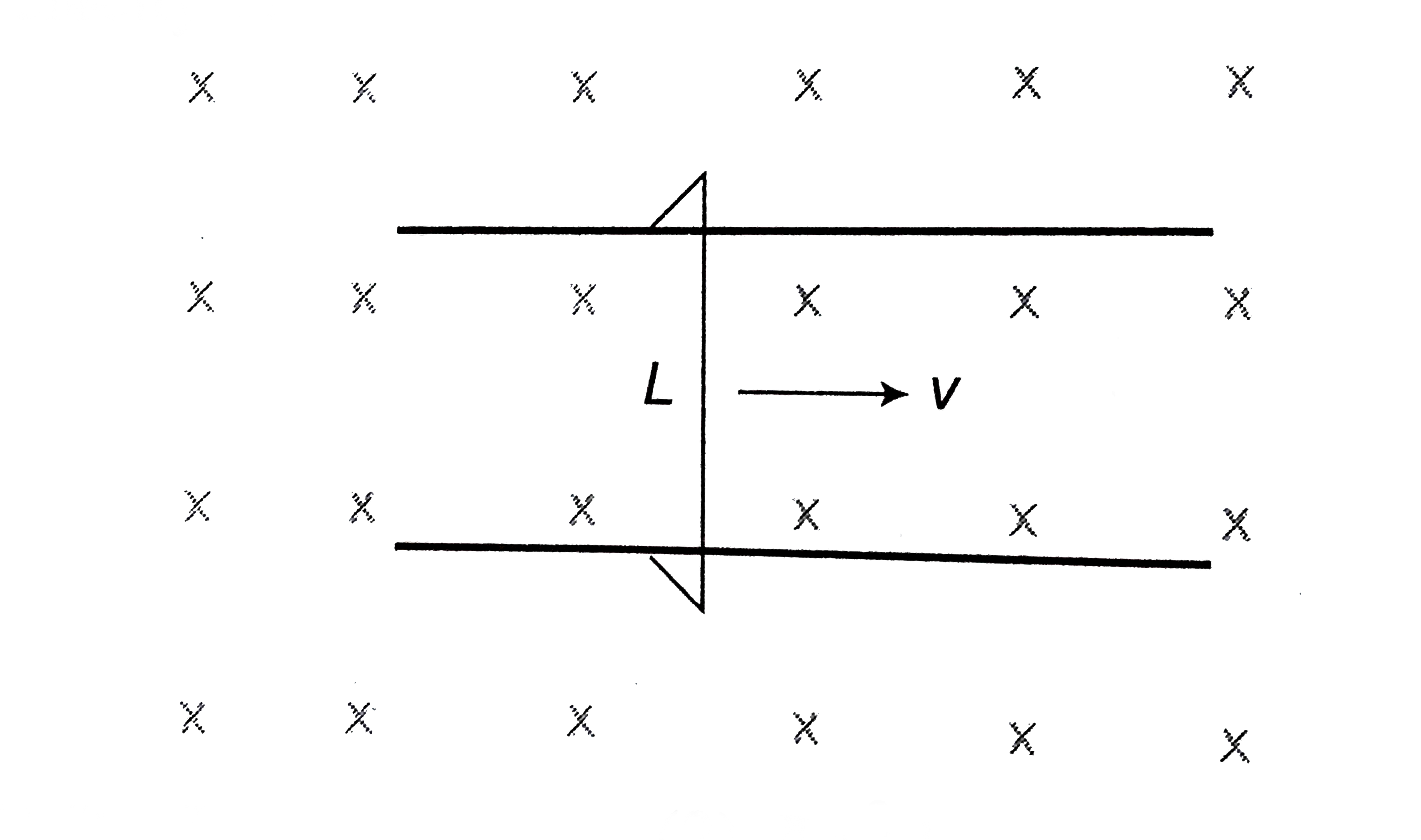
View SolutionIn a metal wire of mass m=24.1 mg can slide with negligible friction on two horizontal parallel rails separated by distance d=2.56 cm . The track lies in a vertical uniform magnetic field of magnitude 56.3 m. At time t=0 , device G is connected to the rails . producing a constant current i=9.13 mA in the wire and rails (even as the wire moves). At t=61.1 ms , what are the wire's (a) speed and (b) direction of motion (left or right)?
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
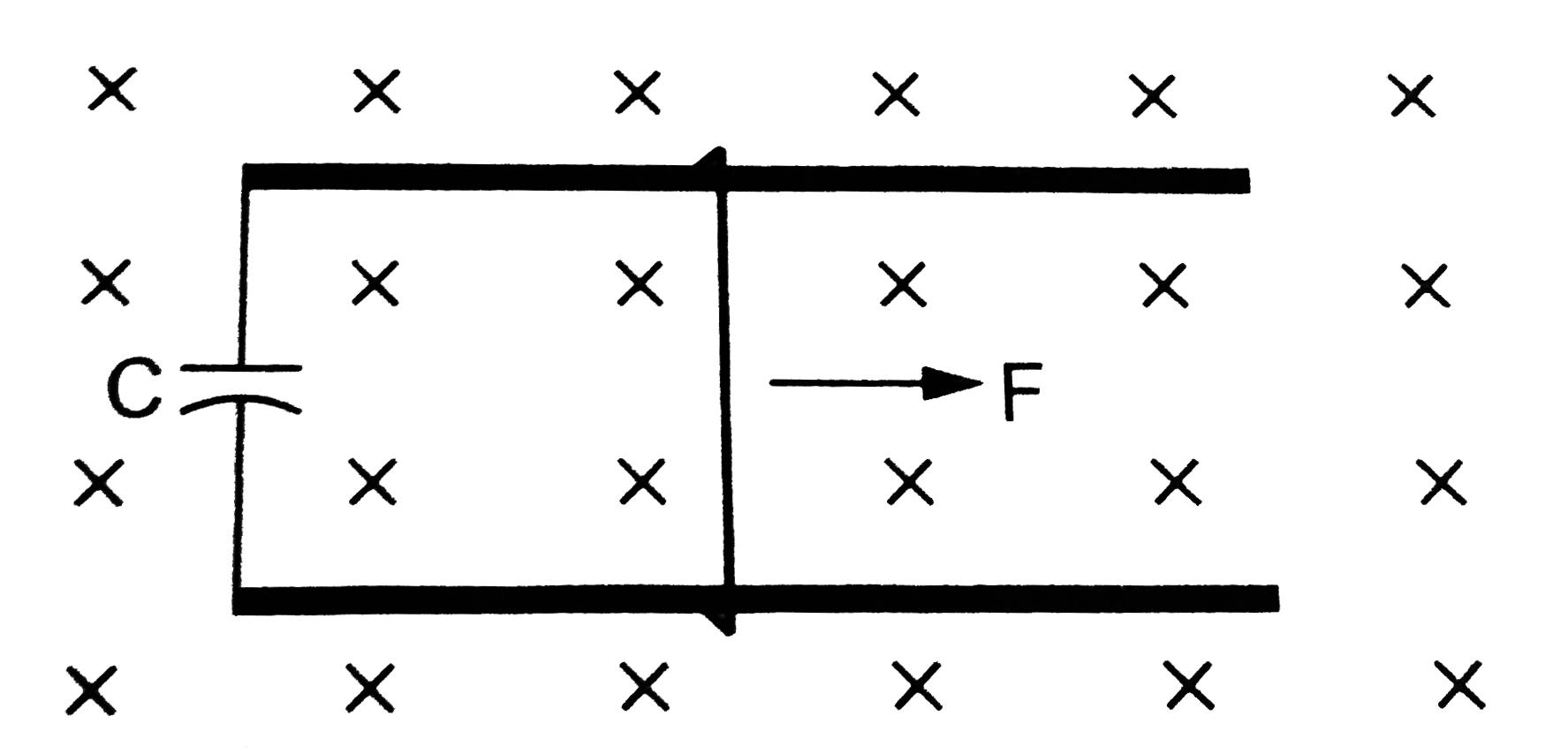
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?

View Solution
