In Fig., find the resultant magnetic force and torque about C, and P.

→Fnet=I2RB . The wire is equivalent to
Forces on each element is radially outward, τC=0
Torque about point P=τp=∫π0[I(RdθBsin90∘]Rsinθ
=2IBR2

Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercise1.3
Explore 14 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercises Subjective
Explore 10 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercise 1.1
Explore 22 Videos
- KINETIC THEORYBook:CENGAGE PHYSICSChapter:KINETIC THEORYExercise:Question Bank
Explore 31 Videos
- Magnetism and MatterBook:CENGAGE PHYSICSChapter:Magnetism and MatterExercise:Question Bank
Explore 50 Videos
Similar Questions
In the figure shown find the resultant magnetic force and torque about ‘C’, and ‘P’.
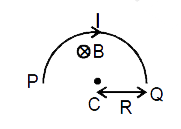
View SolutionIn the figure shown find the resultant magnetic force and torque about 'C' and 'P'.
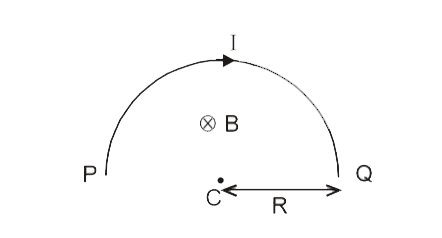
View SolutionFind the resultant magnetic force and torque on the loop.
View SolutionIn Fig., a semicircular wire is placed in a uniform field →B directed towards right. Find the resultant magnetic force and torque on it.

View SolutionMagnetic Moment and Torque
View SolutionFind resultant magnetic field at C in Fig
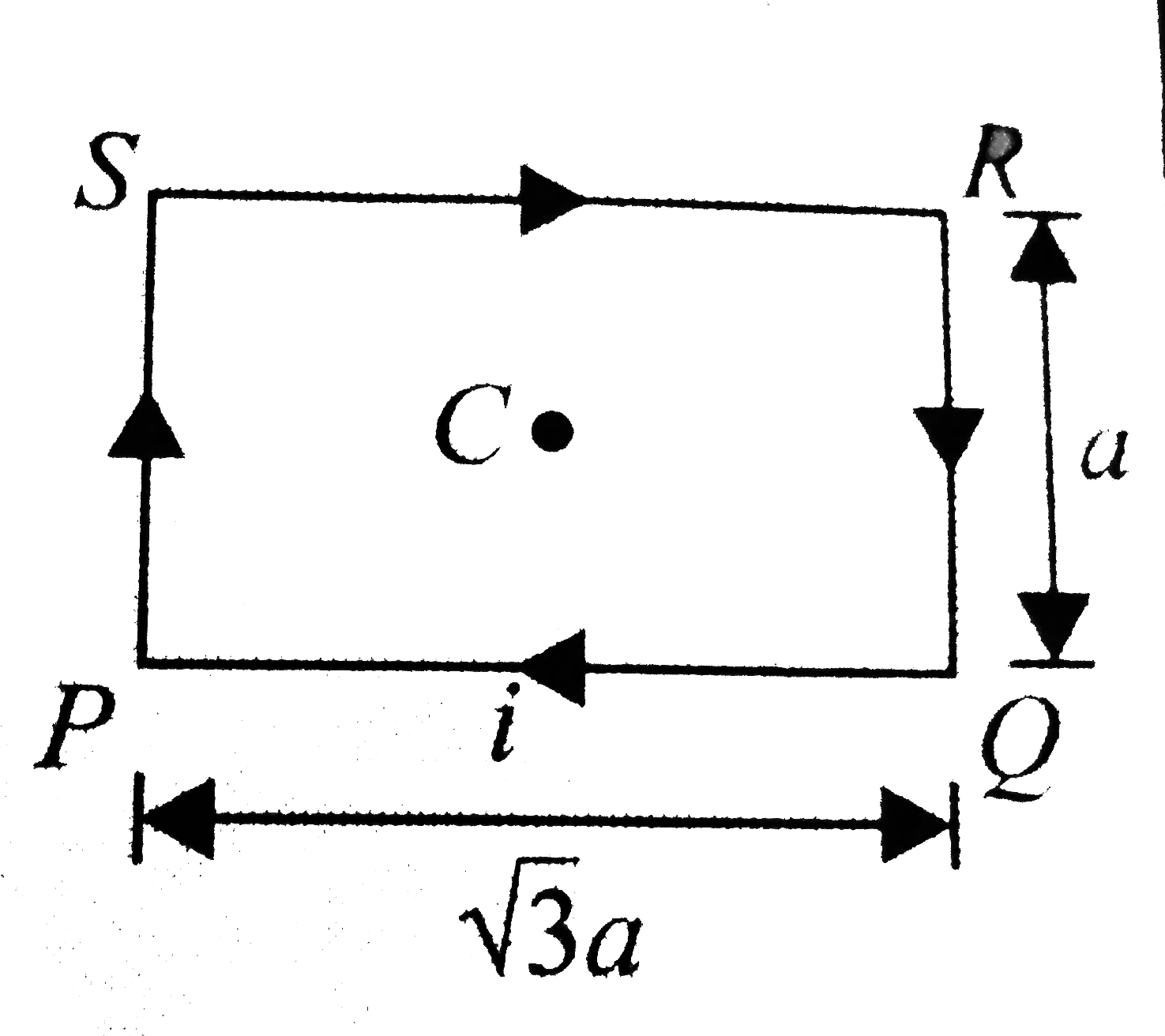
View SolutionWrite down torque about A, B, C
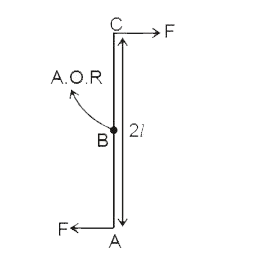
View SolutionIn Fig, find the magnetic field at point P.

View SolutionIn Fig. Find the magnetic field at common centre.

View SolutionIf several forces act on a particle, the total torque on the particle mauy be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces actin on difeent partivles of a body in such a way that their lines of acting intersect at a common point?
View Solution

