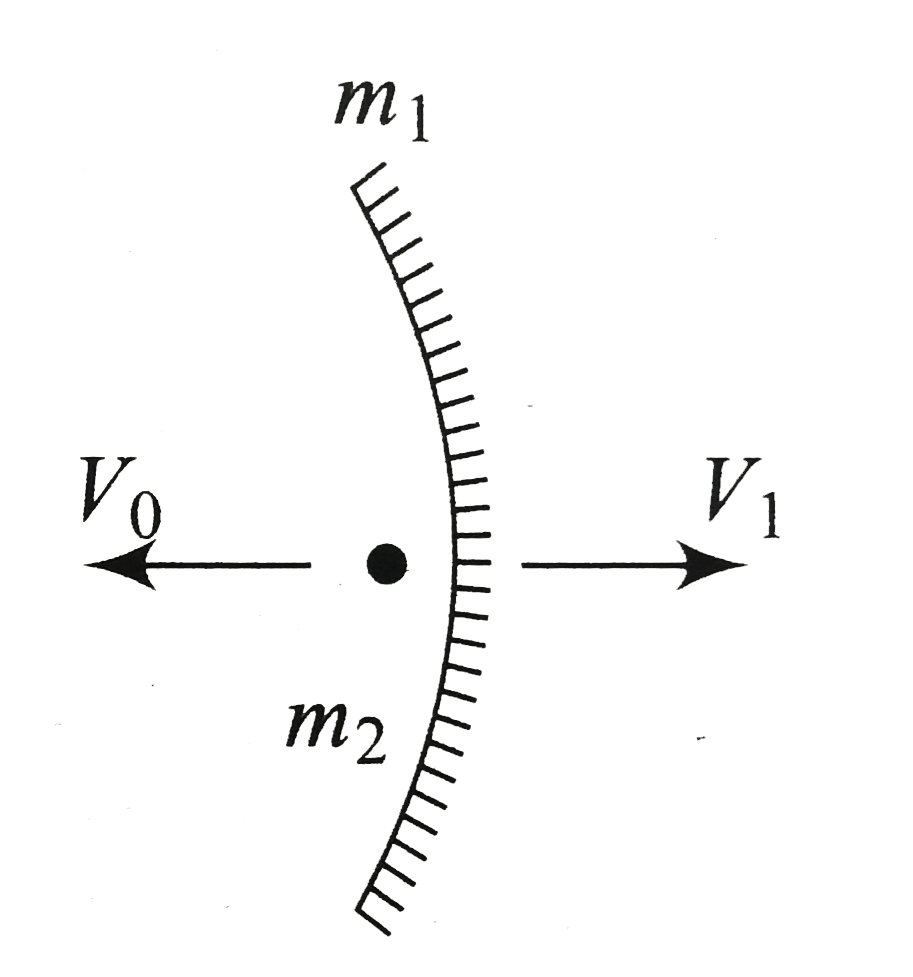
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
(1+m2m1)v0
2(1−m2m1)v0
2(1+2m2m1)v0
2(1+m2m1)v0
The correct Answer is:D
Let v1 be the speed of gun (or mirror) just after the firing of bullet. From conservation of linear momentum,
m2v0=m1v1
v1=m2v0m1 (i)
Now rate at which distance between mirror and bullet is increasing,
dudt=v1+v0 (ii)
dvdt=(v2u2)dudv
Here, v2u2=m2=1
(as at the itme of firing, the bullet is at pole).
dvdt=dudt=v1+v0 (iii)
Here, dv/dt is the rate at which distance between image (of bullet) and mirror is increasing . So, if v2 is the absolute velocity of image (towards right), then
v2−v1=dvdt=v1+v0
or v2=2v1+v0 (iv)
Therefore, speed of separation of the bullet and the image will be
vr=v2+v0=2v1+v0+v0
vr=2(v1+v0)
Substituting value of v1 from Eq. (i), we have
vr=2(1+m2m1)v0
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
View SolutionA gun of mass 1kg fires a bullet of mass 10gm with a Kinetic energy 200J .The velocity of recoil of the gun is?
View Solution
Knowledge Check
A loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
A(a) moves with velocity vMmB(b) moves with velocity vmmcosθ in the horizontal directionC(c) does not move in horizontal directionD(d) moves with velocity v(M−m)M+m in the horizontal directionA gun of mass 20 kg has bullet of mass 0.1 kg in it. The gun is free to recoil and 804 J of recoil energy is released on firing the gun. The speed of bullet (in ms−1) is
A√804×2010B√2010804C√8042010D√804×4×103A man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. By what velocity the gun rebounds backwards
A0.1m/sB10m/sC1m/sD0.01m/s
A gun of mass 4 kg initially at rest fires a bullet of mass 4g with a speed of 50m/s as seen by an observer on ground. Find the impulse on bullet and recoil speed of the gun.
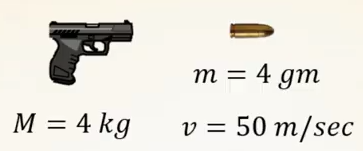
View SolutionA gun fires a bullet of mass 50 g with a velocity of 30 m s−1 because of which the gun recoils with a velocity 1 m s−1. Find the mass of the gun.
View SolutionA gun fires a bullet of mass 50 g with a velocity of 30 m s−1 because of which the gun recoils with a velocity 1 m s−1. Find the mass of the gun.
View SolutionA gun fires a bullet of mass 50g with a velociy of 30m/s. Due to this, the gun is pushed back with a velocity of 1m/s, then the mass of the gun is :
View SolutionA gun fires two bullets at 60∘and30∘ with the horizontal. The bullets strike at some horizontal distance. The ratio of maximum height for the two bullet is
View Solution
