A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
The correct Answer is:A, B
Let v1be the speed of gun (or mirror ) just after the firing of bullet . From conservation of linear momentum,
m2v0=m1v1
or v1=m2v0m1 ...(i)
Now , dudt is the rate at which distance vetween mirror and bullet is increasing =v1+v0 ...(ii)
We have already read in extra points that:
∴dvdt=(v2u2)dudt
Here, v2u2=m2=1 (as at the time of firing,bullet is at pole.)
∴dvdt=dudt=v1+v0

Here, dvdt is the rate at which distance between image (of bullet) and mirror is increasing. So, if
v2is the absolute velocity of image (towards right), then
v2−v1=dvdt
=v1+v0
or v2=2v1+v0
Therefore, speed of separation of bullet and image will be
vr=v2+v0
=2v1+v0+v0
vr=2(v1+v0)
Substituting value of v1 from Eq. (i) we have
vr=2(1+m2m1)v0.
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise 30.1
2 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Introductory Exercise
1 Video
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Example Type 9
2 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
View SolutionA gun of mass 1kg fires a bullet of mass 10gm with a Kinetic energy 200J .The velocity of recoil of the gun is?
View Solution
Knowledge Check
A loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
A(a) moves with velocity vMmB(b) moves with velocity vmmcosθ in the horizontal directionC(c) does not move in horizontal directionD(d) moves with velocity v(M−m)M+m in the horizontal directionA gun of mass 20 kg has bullet of mass 0.1 kg in it. The gun is free to recoil and 804 J of recoil energy is released on firing the gun. The speed of bullet (in ms−1) is
A√804×2010B√2010804C√8042010D√804×4×103A man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. By what velocity the gun rebounds backwards
A0.1m/sB10m/sC1m/sD0.01m/s
A gun of mass 4 kg initially at rest fires a bullet of mass 4g with a speed of 50m/s as seen by an observer on ground. Find the impulse on bullet and recoil speed of the gun.
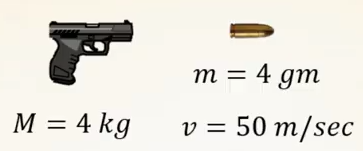
View SolutionA gun fires a bullet of mass 50 g with a velocity of 30 m s−1 because of which the gun recoils with a velocity 1 m s−1. Find the mass of the gun.
View SolutionA gun fires a bullet of mass 50 g with a velocity of 30 m s−1 because of which the gun recoils with a velocity 1 m s−1. Find the mass of the gun.
View SolutionA gun fires a bullet of mass 50g with a velociy of 30m/s. Due to this, the gun is pushed back with a velocity of 1m/s, then the mass of the gun is :
View SolutionA gun fires two bullets at 60∘and30∘ with the horizontal. The bullets strike at some horizontal distance. The ratio of maximum height for the two bullet is
View Solution