An object is placed in front of a convex mirror at a distance of 50cm. A plane mirror is introduced covering the lower half of the convex mirror. If the distance between the object and the plane mirror is 30cm, it is found that there is no parallax between the images formed by the two mirrors. What is the radius of curvature of the convex mirror?
25cm
7cm
18cm
27cm
The correct Answer is:a.
To solve the problem step by step, we will follow the information given in the question and the principles of optics.
Step 1: Understand the setup
We have an object placed in front of a convex mirror at a distance of 50 cm. A plane mirror is placed such that it covers the lower half of the convex mirror, and the distance from the object to the plane mirror is 30 cm.
Step 2: Determine the position of the plane mirror
Since the object is 50 cm from the convex mirror and the distance from the object to the plane mirror is 30 cm, we can find the distance from the convex mirror to the plane mirror:
- Distance from the convex mirror to the plane mirror = Distance from the object to the convex mirror - Distance from the object to the plane mirror
- Distance from the convex mirror to the plane mirror = 50 cm - 30 cm = 20 cm
Step 3: Find the image formed by the plane mirror
A plane mirror forms an image at the same distance behind the mirror as the object is in front of it. Therefore, the image formed by the plane mirror will be:
- Image distance (V_plane) = - Distance from the plane mirror to the object = -30 cm (the negative sign indicates that the image is virtual and located behind the mirror).
Step 4: Find the image formed by the convex mirror
The image formed by the convex mirror can be calculated using the mirror formula:
1f=1v+1u
where:
- u=−50 cm (object distance for the convex mirror, negative as per sign convention),
- v is the image distance for the convex mirror (which we need to find),
- f is the focal length of the convex mirror.
Step 5: Establish the condition of no parallax
Since there is no parallax between the images formed by the two mirrors, the image distance from the convex mirror must equal the distance of the image formed by the plane mirror:
- Therefore, v=−10 cm (the image distance from the convex mirror).
Step 6: Substitute values into the mirror formula
Now we can substitute the known values into the mirror formula:
1f=1−10+1−50
Calculating the right-hand side:
1f=−110−150
Finding a common denominator (which is 50):
1f=−550−150=−650=−325
Thus,
f=−253 cm≈−8.33 cm
Step 7: Calculate the radius of curvature
The radius of curvature R is related to the focal length f by the formula:
R=2f
Substituting the value of f:
R=2×−253=−503 cm≈−16.67 cm
Since the radius of curvature is taken as a positive quantity, we can state:
R=503 cm≈16.67 cm
Final Answer:
The radius of curvature of the convex mirror is approximately 16.67 cm.
We have an object placed in front of a convex mirror at a distance of 50 cm. A plane mirror is placed such that it covers the lower half of the convex mirror, and the distance from the object to the plane mirror is 30 cm.
Since the object is 50 cm from the convex mirror and the distance from the object to the plane mirror is 30 cm, we can find the distance from the convex mirror to the plane mirror:
- Distance from the convex mirror to the plane mirror = Distance from the object to the convex mirror - Distance from the object to the plane mirror
- Distance from the convex mirror to the plane mirror = 50 cm - 30 cm = 20 cm
A plane mirror forms an image at the same distance behind the mirror as the object is in front of it. Therefore, the image formed by the plane mirror will be:
- Image distance (V_plane) = - Distance from the plane mirror to the object = -30 cm (the negative sign indicates that the image is virtual and located behind the mirror).
The image formed by the convex mirror can be calculated using the mirror formula:
1f=1v+1u
where:
- u=−50 cm (object distance for the convex mirror, negative as per sign convention),
- v is the image distance for the convex mirror (which we need to find),
- f is the focal length of the convex mirror.
Since there is no parallax between the images formed by the two mirrors, the image distance from the convex mirror must equal the distance of the image formed by the plane mirror:
- Therefore, v=−10 cm (the image distance from the convex mirror).
Now we can substitute the known values into the mirror formula:
1f=1−10+1−50
Calculating the right-hand side:
1f=−110−150
Finding a common denominator (which is 50):
1f=−550−150=−650=−325
Thus,
f=−253 cm≈−8.33 cm
The radius of curvature R is related to the focal length f by the formula:
R=2f
Substituting the value of f:
R=2×−253=−503 cm≈−16.67 cm
Since the radius of curvature is taken as a positive quantity, we can state:
R=503 cm≈16.67 cm
The radius of curvature of the convex mirror is approximately 16.67 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Assertion-Reasoninig
Explore 2 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Linked Comprehension
Explore 51 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Subjective
Explore 26 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
A convex mirror and a plane mirror are arranged facing an object as shown in the figure below. If there is no parallax between the images formed by the two mirrors, then find the radius of curvature of the convex mirror?
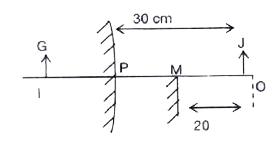
View SolutionAn object is placed on the principal axis of a convex mirror of focal length 15 cm. If the distance of the object from the mirror is 30 cm, where should a plane mirror be placed such that the images produced by the two mirrors coincide?
View Solution
Knowledge Check
An object is placed in front of a convex mirror at a distance of 50cmA p[lane mirror is introduced covering the lower half of the convex mirror.If the distance between the images formed by the two mirrors .The radius of the convex is :
A12.5cmB25cmC50cmD100cmAn object of height 0.5 m is placed in front of convex mirror. Distance of object from the mirror is equal to the focal length of the mirror. Height of the image of the object is
AinfiniteB1 mC0.25 mD0.5 mAn object is placed in front of a convex mirror at a point between infinity and the pole of the mirror . The image formed is
Areal and enlarged.Bvirtual and enlargedCreal and diminshedDvirtual and diminished
An object is placed in front of a convex mirror of a radius of curvature 20 cm. Its image is formed 8 cm behind the mirror. The object distance is
View SolutionAn object is placed 10 cm in front of a convex mirror of focal length 20 cm . The distance of the image from the mirror is
View SolutionAn object is placed at a distance of 10 cm in front of a plane mirror, then the distance of image from mirror is:
View SolutionAn object is placed in front of a convex mirror at a distance equal to the focal length of the mirror. If its focal length is 20 cm, the distance of the image from the mirror is ______ cm
View SolutionAn object is placed at a large distance in front of a convex mirror of radius of curvature 40 cm . What is the distance of image from the mirror ?
View Solution

