The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
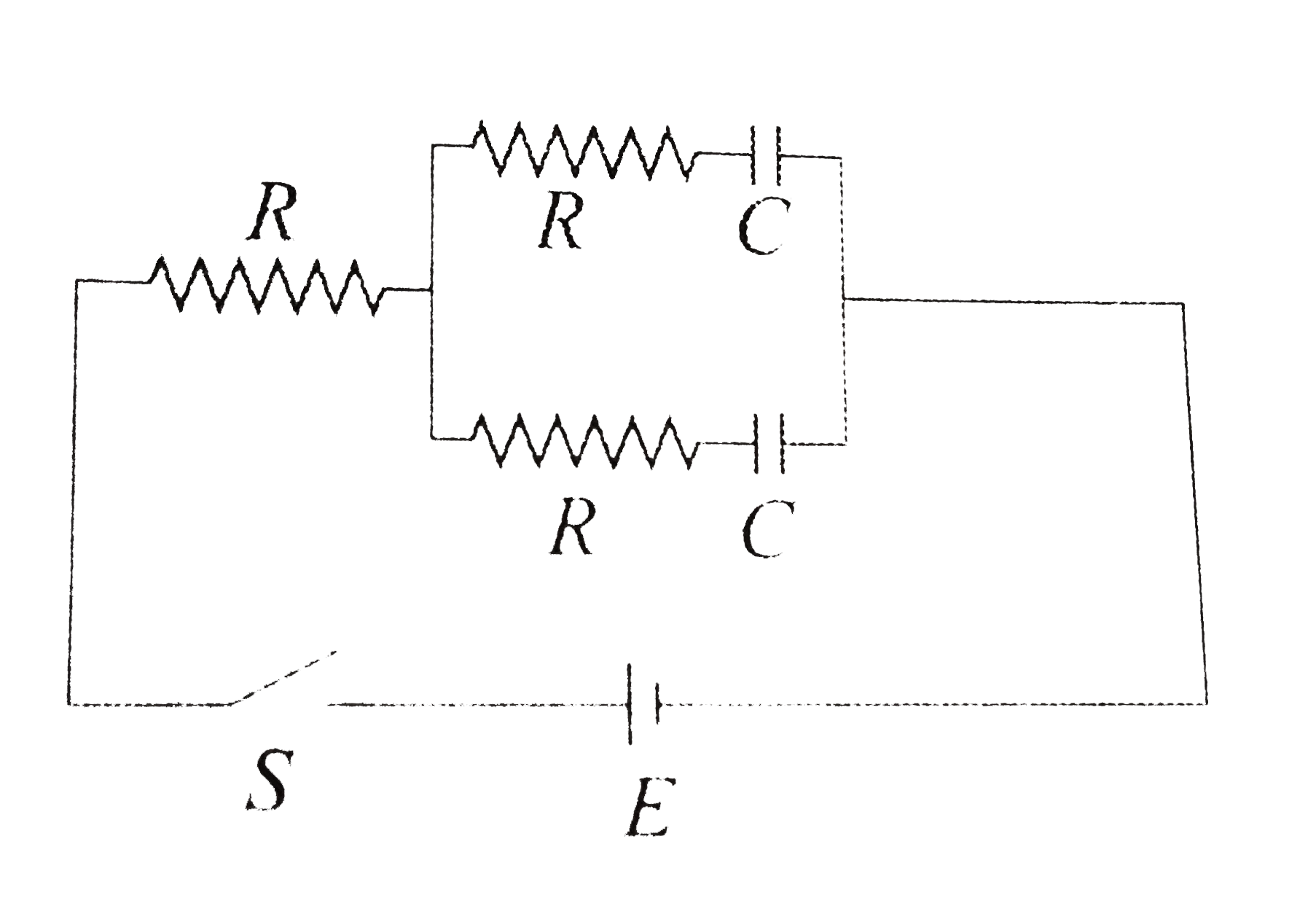
qt=EC(1−e−2t/3RC)
qt=EC(1−e−t/2RC)
qt=EC(1−e−t/3RC)
qt=EC(1−e−3t/2RC)
The correct Answer is:C
c. Applying KVL, we get
12=dqdtorI=2dqdt
E−IR−12R−qC=0
or E−32IR−qC=0
or E−32×2dqdtR−qC=0
qt=EC(1−e−t/3RC).
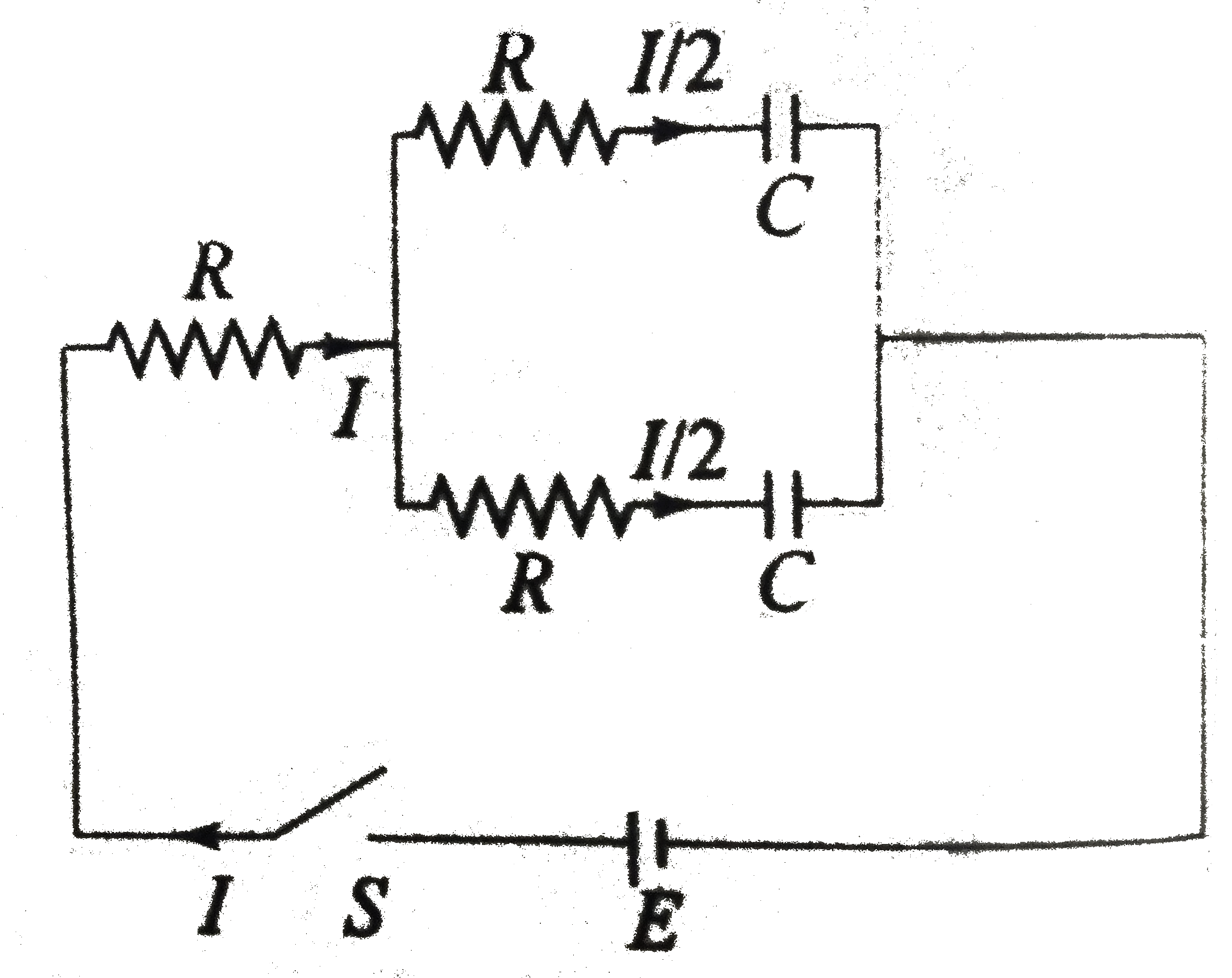
Similar Questions
In the given circuit, the switch S is closed at time t = 0 . The charge Q on the capacitor at any instant t is given by Q(t)=Q(1−e−αt). Find the value of Q0 and α in terms of given parameters as shown in the circuit.
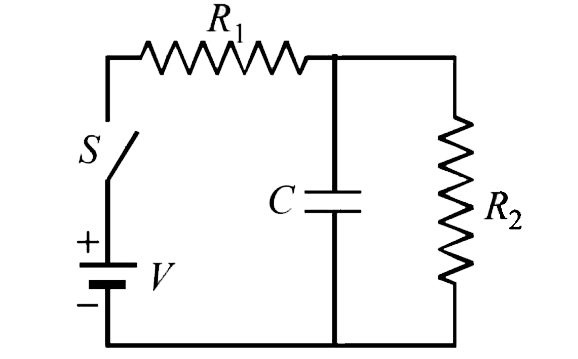
. View SolutionIn the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by (Ceq=C1C2C1+C2)
View Solution
Knowledge Check
- Question 1 - Select One
The switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
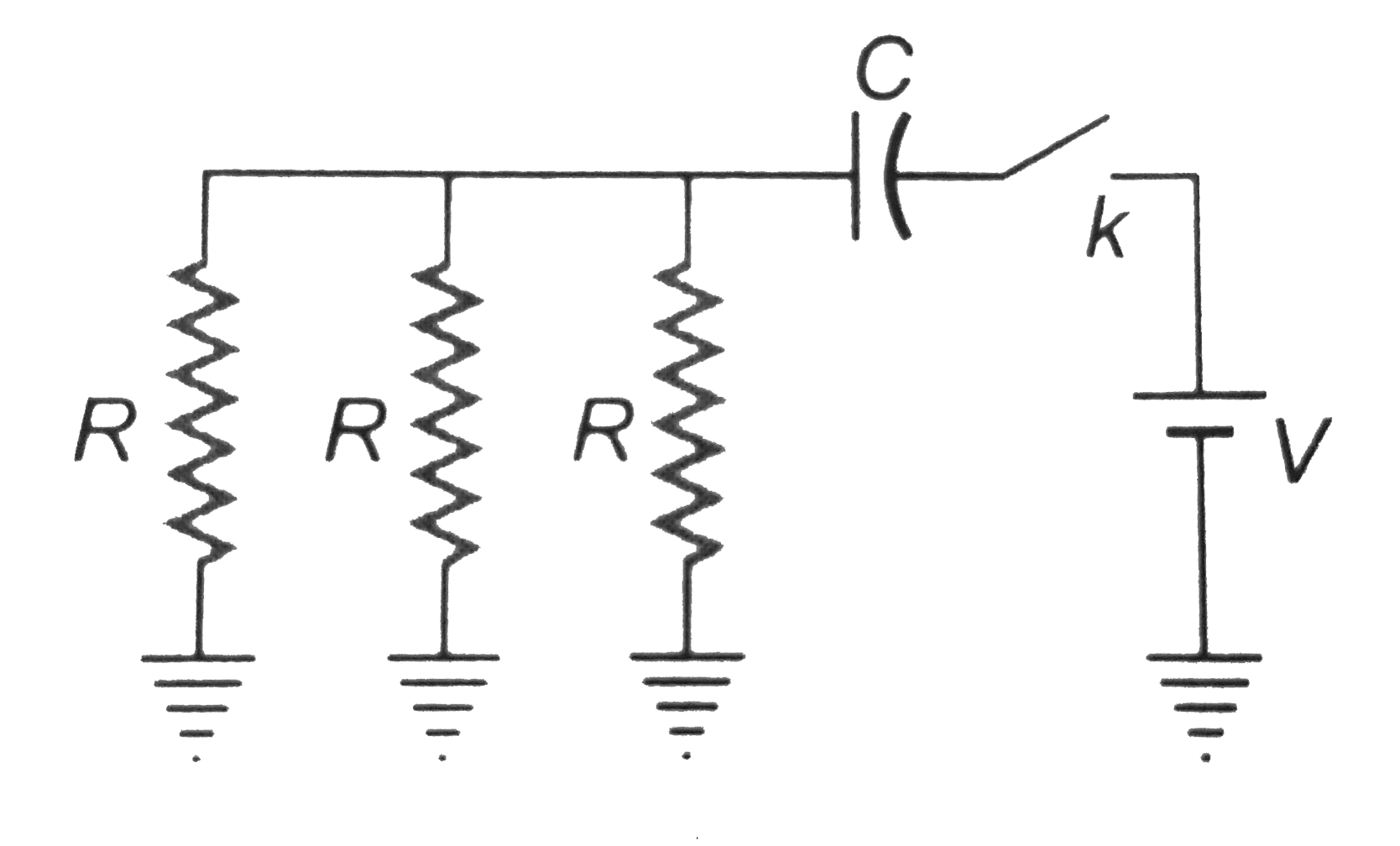ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC) - Question 2 - Select One
In given circuit, switch S is closed at t=0 . The charge on the capacitor ar steady state will be
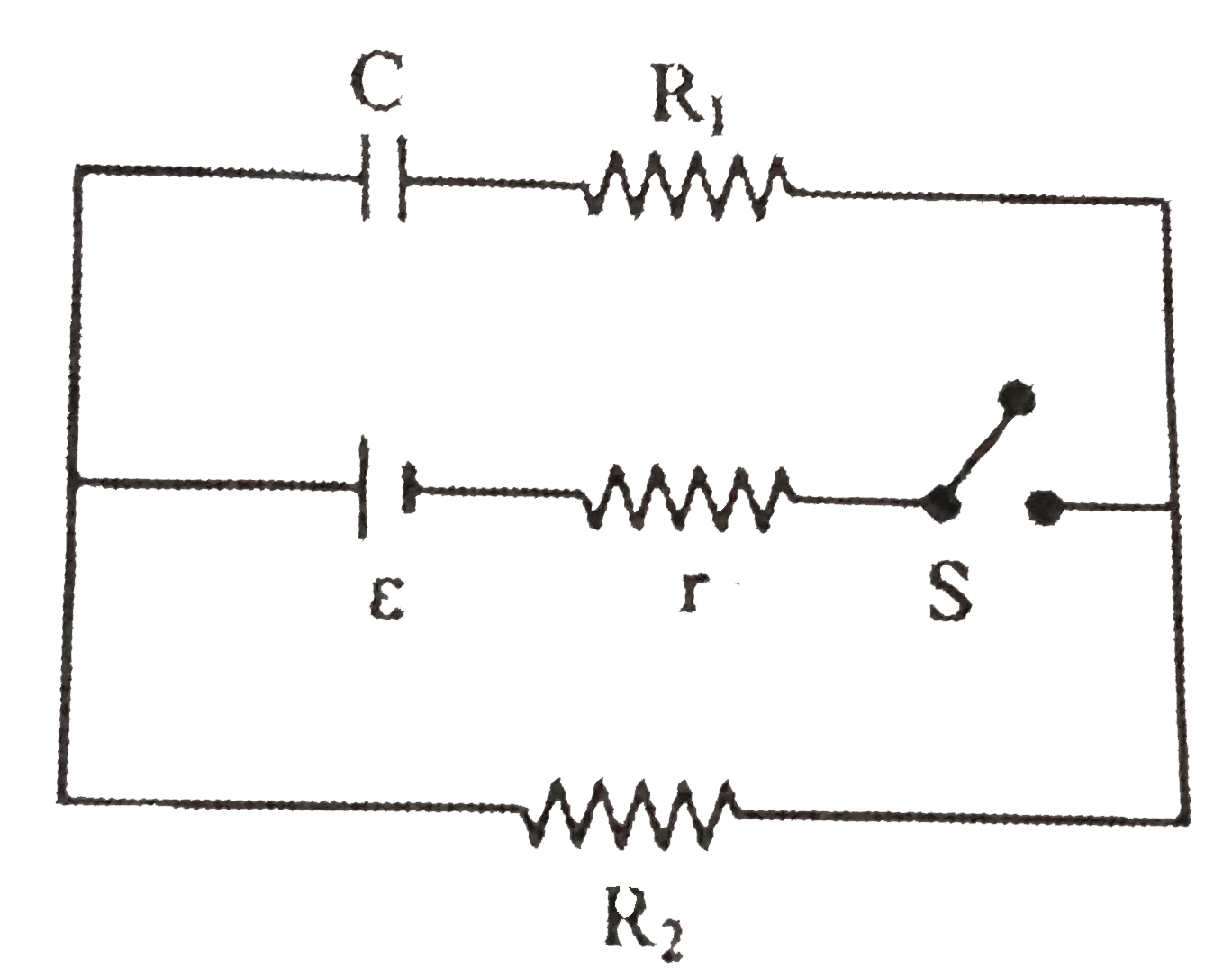ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2 - Question 3 - Select One
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
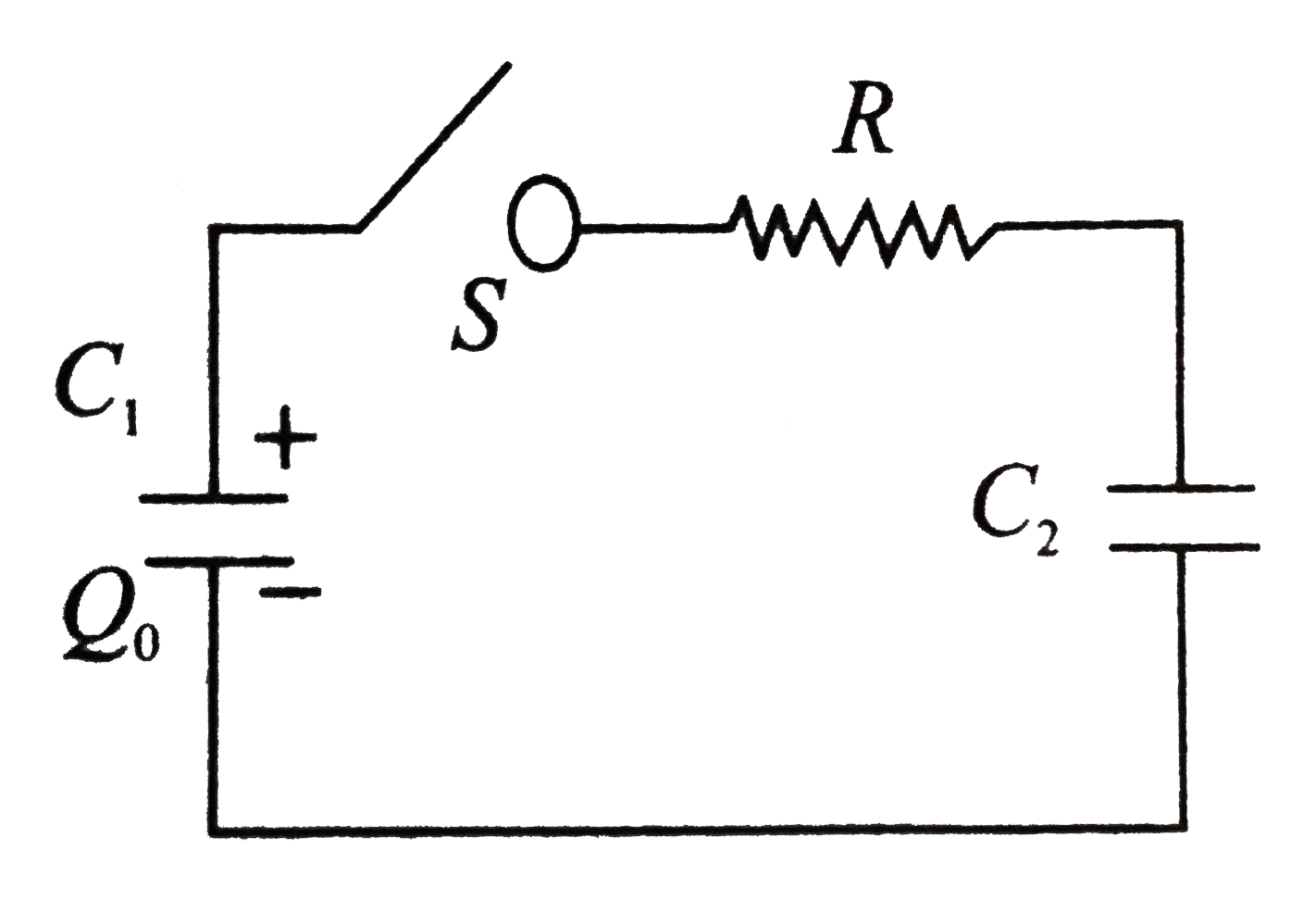Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
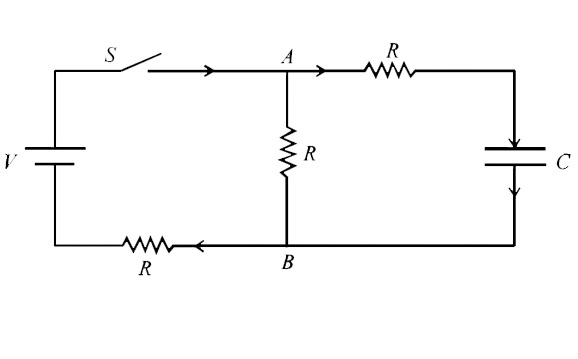
In the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
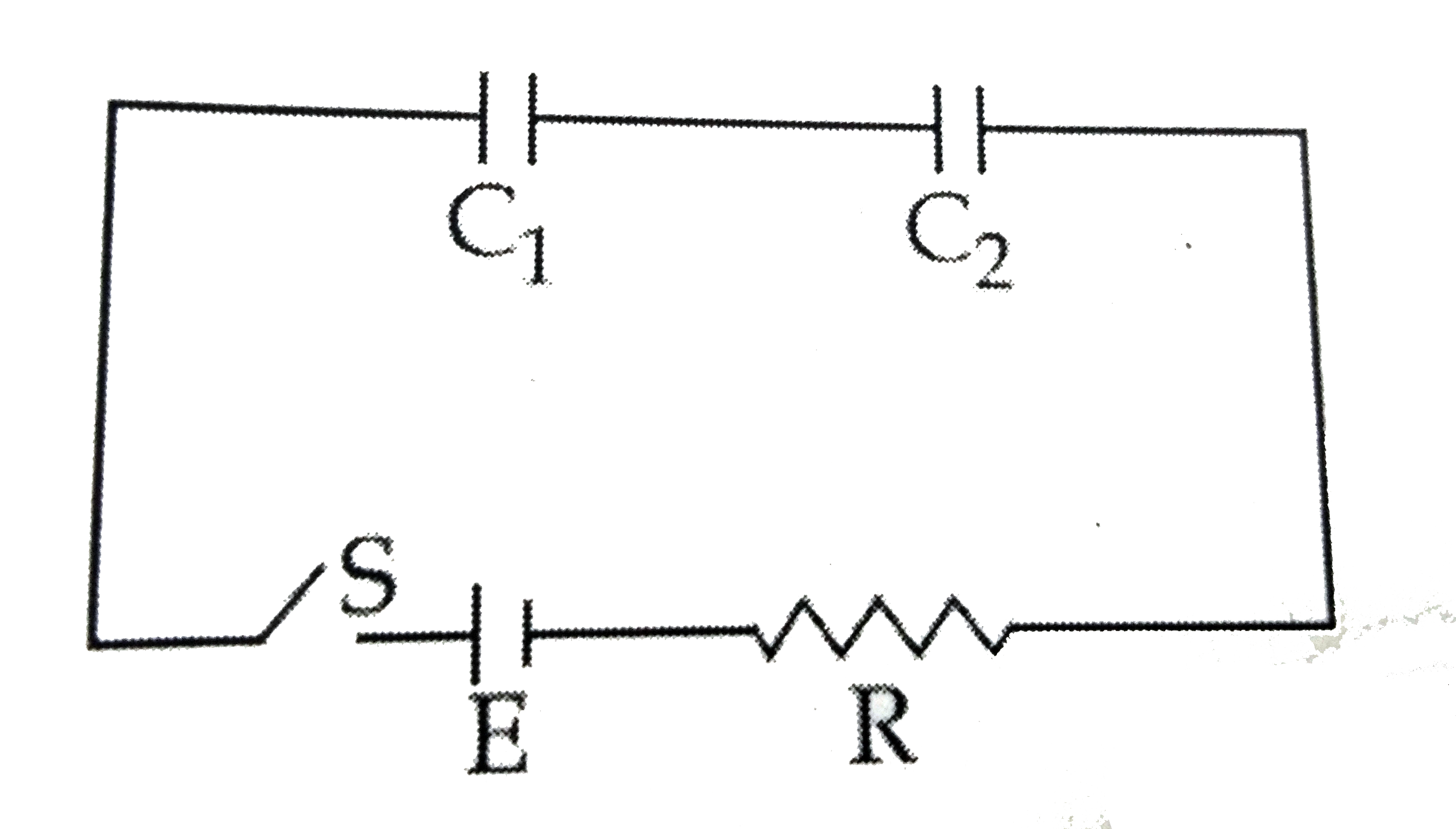
. View SolutionThe switch S of the circuit is closed at t = 0. Find the current (in Amp.) through the capacitor when the switch S is closed at t = 0
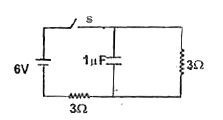
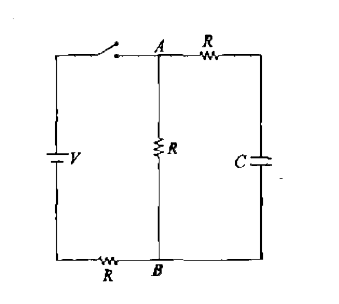
View SolutionIn the circuit shown in figure-3.244, the battery is an ideal one with emf V. The capacitor is initially uncharged. The switch S is closed at time t=0.
(a) Find the charge Q on the capacitor at time l
(b) Find the current in branch AB at time just after closing the switch.
View SolutionConsider two circuits given below. When switches S1andS2 are closed at t=0, the charge on capacitors C1 and C2 change with time as shown in graph 1 and 2 respectively. The current i1 and i2 in the two circuits change as shown in graph 1' & 2' respectively. Write the variation of current in the second circuit as function of time after the switch is closed at t=0.e−1=0.37
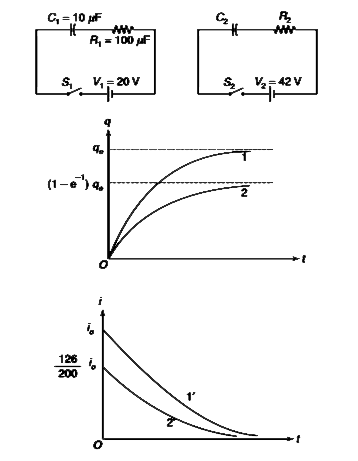
View SolutionTwo plates of a charged capacitor are connected to each through a resistance and a switch which is kept open initially. The switch is closed at t= 0. If q is charge on capacitor and I is the current in the circuit at time t then the curves that correctly represent the variation of the change and current with time are:
View Solution