A cubical region of side a has its centre at the origin. It encloses three fixed point charges, −q at (0,−a/4,0), +3q at (0,0,0) and −q at (0,+a/4,0). Choose the correct options(s)
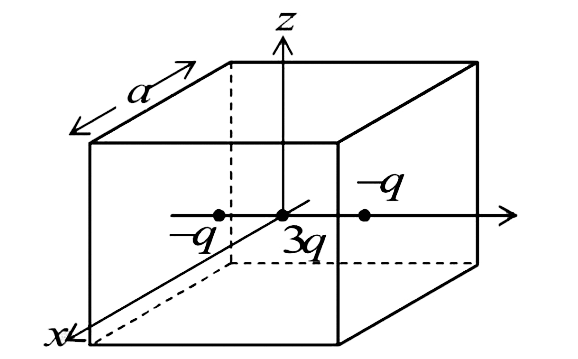
The net electric flux crossing the plane x=+a/2 is equal to the net electric flux crossing the plane x=−a/2 .
The net electric flux crossing the plane y=+a/2 is more than the net electric flux crossing the plane y=−a/2.
The net electric flux crossing the entire origin is q/ε0.
The net electric flux crossing the plane z=+a/2 is equal to the net electric flux crossing the plane x=+a/2 .
Position of all the charges are symmetric about the planes x=+a/2 and x=−a/2. So net electric flux then will be same. Similarly, flux through y=+a/2is equal to flux through y=−a/2/
ϕ=q∈ε0=3q−q−qε0=qesπlon0
By symmetry flux through z=+q/2 is equal to flux through x=+q/2
Similar Questions
Consider a spherical surface of radius 4 m cenred at the origin. Point charges +q and - 2q are fixed at points A( 2 m, 0,0) and B( 8 m, 0, 0), respectively. Show that every point on the shperical surface is at zero potential.
View SolutionA charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P (0,0,3 cm) to a point Q (0,4 cm, 0) via a point R (0,6 cm, 9cm).
View Solution
Knowledge Check
A cubical region of side a has its centre at the origin. It encloses three point charges , −q at (0,−a/4,0),+3qat(0,0,0) and −q at (0,+a/4,0).
Choose the correct option (s)
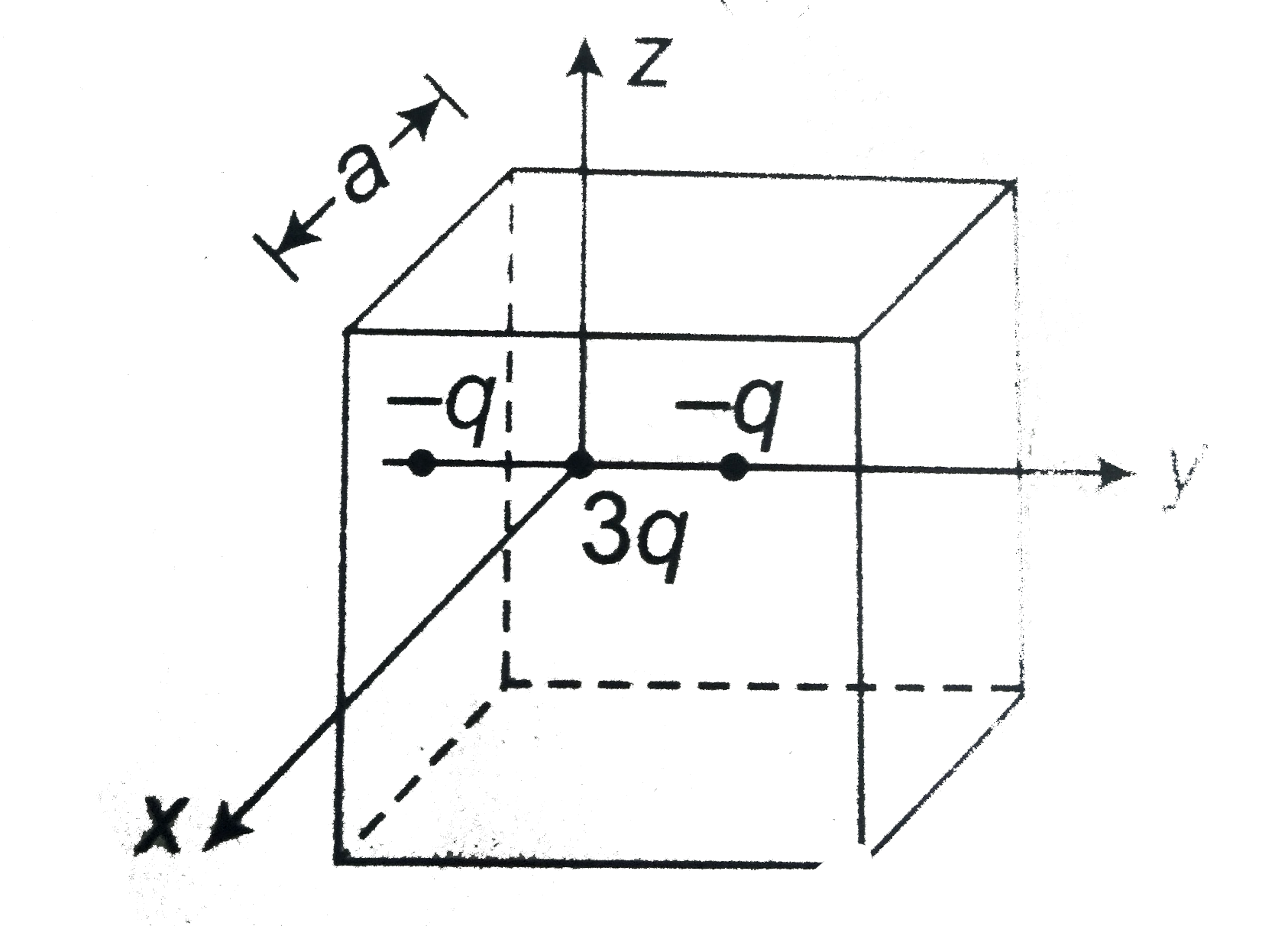
(i) The net electric flux crossing the plane x=+q2 is equal to the net electric flux crossing the plane x=−a2
(ii) The net electric flux crossing the plane y=+a2 is more than the net electric flux crossing the plane y=−a2
(iii) The net electric flux crossing the entire region is qε0
(iv) The net electric flux crossing the plane z=+a2 is equal to the net electric flux crossing the plane x=+a2A(i),(ii)B(i),(iii)C(i),(iii),(iv)D(ii),(iii),(iv)A regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
AZeroBkQaC12kQaD6kQaA point charge q1=−1.0μC is held stationary at the origin. A second point charge q2=+2.0μC moves from the point (1.0m,0,0) to (2.0m,0,0). How much work is done by the electric force on q2?
A9mJB−9mJC−18mJD18mJ
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9 from a point P(0,0,3cm) to a point Q (0,4cm,0) via a point R(0,6cm,9cm).
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA point charge q1=−5.8μC is held stationary at the origin. A second point charge q2=+4.3μC moves from the pont (0.26m0,0) to (0.38m,0,0). How much work is doen the electric force on q2?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
View Solution
