Two fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
Points where the electric potential due to the two charges is zero in x-y plane, lie on a circle radius 4a and centre (5a,0)
potential is zero at x=a and x=9a
both a and b are wrong
both a and b are correct
The correct Answer is:D
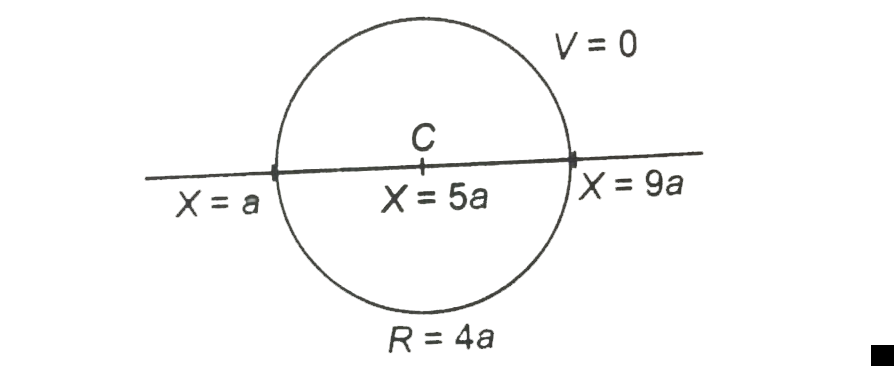
Let P=(x,y)
r1=√(x+3a)2+y2
r2=√(x−3a)2+y2
Vp=14πε0[Qr2−2Qr1]=0 ……..i
Sustituting vaues of r1 and r2 in eqn i we can see that equation is of a circle of radius 4a and centre of 5a.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Two fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
Show that all points in the x-y plane where the electric potential due to the two charge is zero , lie on a circle. If its radius is r = xa and the location of its centre is (ya,0) find x and y .
View SolutionTwo fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
If a particle of charge +q starts from rest at the centre of the circle , show by a short quantitavtive argument that the particle eventually crosses the circle . If its speed V=√Qqzπε0ma , then find z.
View Solution
Knowledge Check
Two fixed charges −2Q and Q are locatted at the points with coordinates ( -3 a, 0) and (+3 a, 0) prespectively in the X−Y plane .
All the points in the X−Y plane where the electric potential due to the two charges is zero , line on a .Astraight lineBcircleCparabolaDellipseTwo fixed charges −2Q and Q are locatted at the points with coordinates ( -3 a, 0) and (+3 a, 0) prespectively in the X−Y plane .
The expression for the potential V(x) at a general point on the x-axis is given by .AV(x)=14πɛ0[Q3a−x−2Q(3a+x)]for0<x<3aBV(x)=14πɛ0[2Q3a−x−2Q(3a+x)]for0<x<3aCV(x)=14πɛ0[Q3a−x−2Q(3a+x)]for0<x<3aDV(x)=14πɛ0[Q3a−x−2Q(3a+x)]for0<x<3aTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) resepctively.The electric potential at point (0,0,z)is (Z>a)
Aqa4πε0z2Bq4πε0aC2qa4πε0(z2−a2)D2qa4πε0(z2+a2)
Two charges of magnitude −2Qand+Q are located at points (a,0) and (4a, 0) respectively ,What is the electric flux due to these charges through a sphere of radius 3a with its centre at the origin?
View SolutionTwo charges of magnirude −2Qand+Q are located at points (a,0)and(4a,0) respectively .
What is the electric flux due to charges through a sphere of radius '3a' with its center at the origin.
View SolutionTwo charges −2Q abd Q are located at the points with coordinates (−3a,0) and (+3a,0) respectively in the x-y plane. (i) Show that all points in the x-y plane where the electric potential due to the charges is zero, on a circle. Find its radius and the location of its centre (ii) Give the expression V(x) at a general point on the x-axis and sketch the function V(x) on the whole x-axis. (iii) If a particle of charge +q starts from rest at the centre of the circle, shown by a short quantitative argument that the particle eventually crosses the circule. Find its speed when it does so.
View SolutionTwo charges of magnitudes +4Q and -Q and located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius '2a' with its centre at the orgin ?
View SolutionTwo charges - q and + q are located at points A(0, 0, -a) and B(0, 0, +a) respectively. How much work is done in moving a test charge from point P(7,0,0) to Q(-3,0,0) ?
View Solution
