It is desired to make a 20Ω coil of wire, which has a zero thermal coefficient of resistance. To do this, a carbon resitor fo resistane R1 is placed in series with an iron resistor of resistance R2 the proportions of iron and carbon are so chosen that R1+R2=20Ω for all temperatures near 20∘C. How long are R1andR2? αcarbon=−0.5×10−3.∘C−1,αiron=5×10−3.∘C(−1)
We need R−1(1+α1Δt)+R2(1+α2Δt)=20.BecauseR1+R2
=20whenΔt=0, we must have R1α1=−R2α2=−withα1=−0.5
×10−3andα2=5×10−3. Solving the two equations R1+R2
=20 and R1=10R2 simultaneously leads to R1=18.18Ω and
R2=1.82Ω
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.2
Explore 50 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Subjective
Explore 29 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
It is desired to make a 20Omega coil of wire which has a zero thermal coefficient of resistance. To do this, a carbon resistor of resistance R, is placed in series with an iron resistor of resistance R. The proportions of Iron and carbon are so chosen that R1,+R2=20Ω for all temperatures near20∘C. How large are Ri andR2 ? (a−(c)=−0.5×10−3/∘C,afe=5×10−3/∘C)
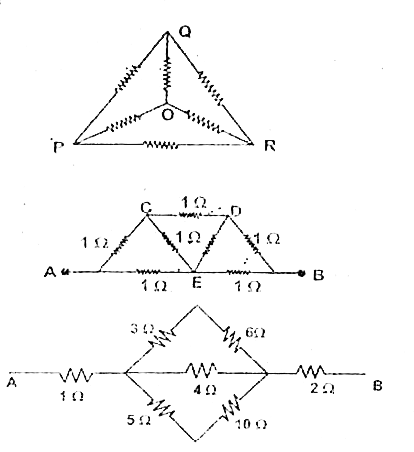
(b) Six equal resistances, each of resistance4Ω are connected to form the following figure. What is the resistance between any two corners?
(c) In the network shown in figuro, each resistance is 1Ω. What is the effective resistance between A and B.
(d) Find the equivalent resistance between points A and B of the network shown in the given diagram.
View SolutionIt is desired to make a 20.0Ω coil of wire whose temperature coefficient of resistance is zero. To do this, a carbon resistor of resistance R1 is placed in series with an iron resistor of resistance R2. The proportion of iron and carbon are so chosen that R1+R2=20Ω for all temperatures near 20∘C. Find the values of R1 and R2. Temperature coefficient of resistance for carbon, αC=−0.5×10−3/∘C and that of iron is αFe=5×10−3/∘C.
View Solution
Knowledge Check
Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>R1+R2BR1<R<R2CR2<R<(R1+R2)DR<R1It is desired to make a long cylindrical conductor whose temperature coefficient of resistivity at 20∘C will be close to zero. If such a conductor is made by assembling alternate disks of iron and carbon, find the ratio of the thickness of a carbon disk to that an iron disk. (For carbon,p=3500×10−8Ωmandα=−0.50×10−3.∘C−1for iron, p=9.68×10−8Ωmandα=6.5×10−3.∘C−1)
A0.36B0.036C1D2Two wires of resistance R1 and R2 have temperature coeficient of resistance α1 and α2 respectively. These are joined in series. The effeictive temperature coefficient of resistance is
Aα1+α22B√α1α2Cα1R1+α2R2R1+R2D√R1R2α1α2√R21+R22
A carbon and an aluminimum wire are connected in series.If the combination has resistance of 27 ohm at 0∘C,what is the resistance of each wire at 0∘C so that the resistance of the combination does not change with temperature ?
[αC=−0.5×10−3(.∘C)−1 and αA=4×10−3(.∘C)−1].
View SolutionWhen two resistors of resistances R1andR2 are connected in parallel, the net resistance is 3Ω. When connected in series, its value is 16Ω. Calculate the values of R1andR2.
View SolutionA potentiometer wire of length 1m has a resistance 20Omega .It is connected in series with a resistance R and a cell of emf 2 volts.If potential gradient is 1V/m .Find R
View SolutionEstablish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R1,R2andR3 connected in series.
(b) Calculate the equivalent resistance R of a combination of three resistors of 2Ω,3Ωand6Ω joined in parallel.
View SolutionA resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View Solution

