The voltage-current variations of two metallic wire X and Y at constant temperature is shown in fig Assumign that the wires have the same length and the same diameter, explain which of the two wires will have larger resisitivity.
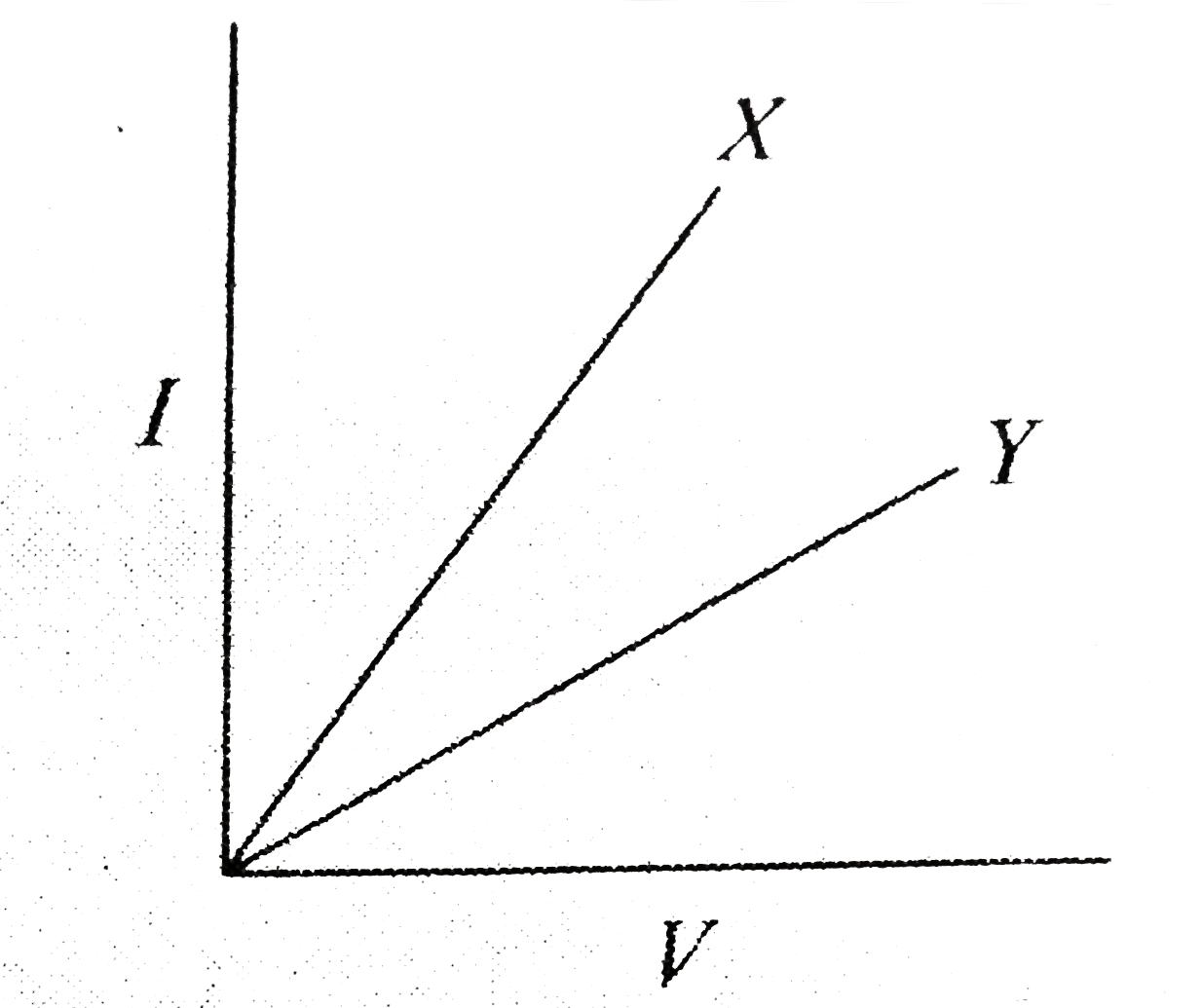
R=ρlA,so ρ∝R.ButRY>RX.
Because for same V, current in Y is less. So ρy>ρx.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.2
50 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
V-I graph for the metallic wires X and Y at constant temperature are as shown in figure:
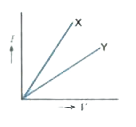
Assuming that the two wires have same length and same diameter, explain as to which of the two wires has higher resistivity and why?
View SolutionTwo copper wires of the same length have got different diameters
a. which wire has greater resistance?
b. greater specific resistance?
View Solution
Knowledge Check
The current (I) and voltage (V) graphs for a given metallic wire at two different temperature (T1) and (T2) are shown in fig. It is concluded that
 AT1=T2BT1>T2CT1<T2DNone of these
AT1=T2BT1>T2CT1<T2DNone of theseWhen two wires have current in same direction then force is
AAttractiveBRepulsiveCBoth attractive and repulsiveDCan't be determinedThe current -voltage - variation for a wire of copper of length (L) and area (A) is shown in fig. The slope of the line will be
 Aless if experiment is done at a heigher temperatureBmore if a wire of silver of same dimension is usedCwill be doubled if the lengths of the wire is doubledDwill be halved if the length is doubled
Aless if experiment is done at a heigher temperatureBmore if a wire of silver of same dimension is usedCwill be doubled if the lengths of the wire is doubledDwill be halved if the length is doubled
Two wires of same material and radius have their lengths in ratio 1 : 2. If these wires are stretched by the same force, the strain produced in the two wires will be in the ratio
View SolutionTwo wires of same material and radius have their lengths in ratio 1 : 2. If these wires are stretched by the same force, the strain produced in the two wires will be in the ratio
View SolutionTwo steel wires of the same radius have their lengths in the ratio of 1:2. If they are stretched by the same force, then the strains produced in the two wires will be in the ratio of
View SolutionTwo wires made from the same metal have radii in the ratio 1:2. If the lengths of wires is the same, their resistances have ratio
View SolutionA copper wire and a steel wire of the same diameter and length are joined end and a force is applied which stretches their combined length by 1 cm. Then, the two wires will have
View Solution