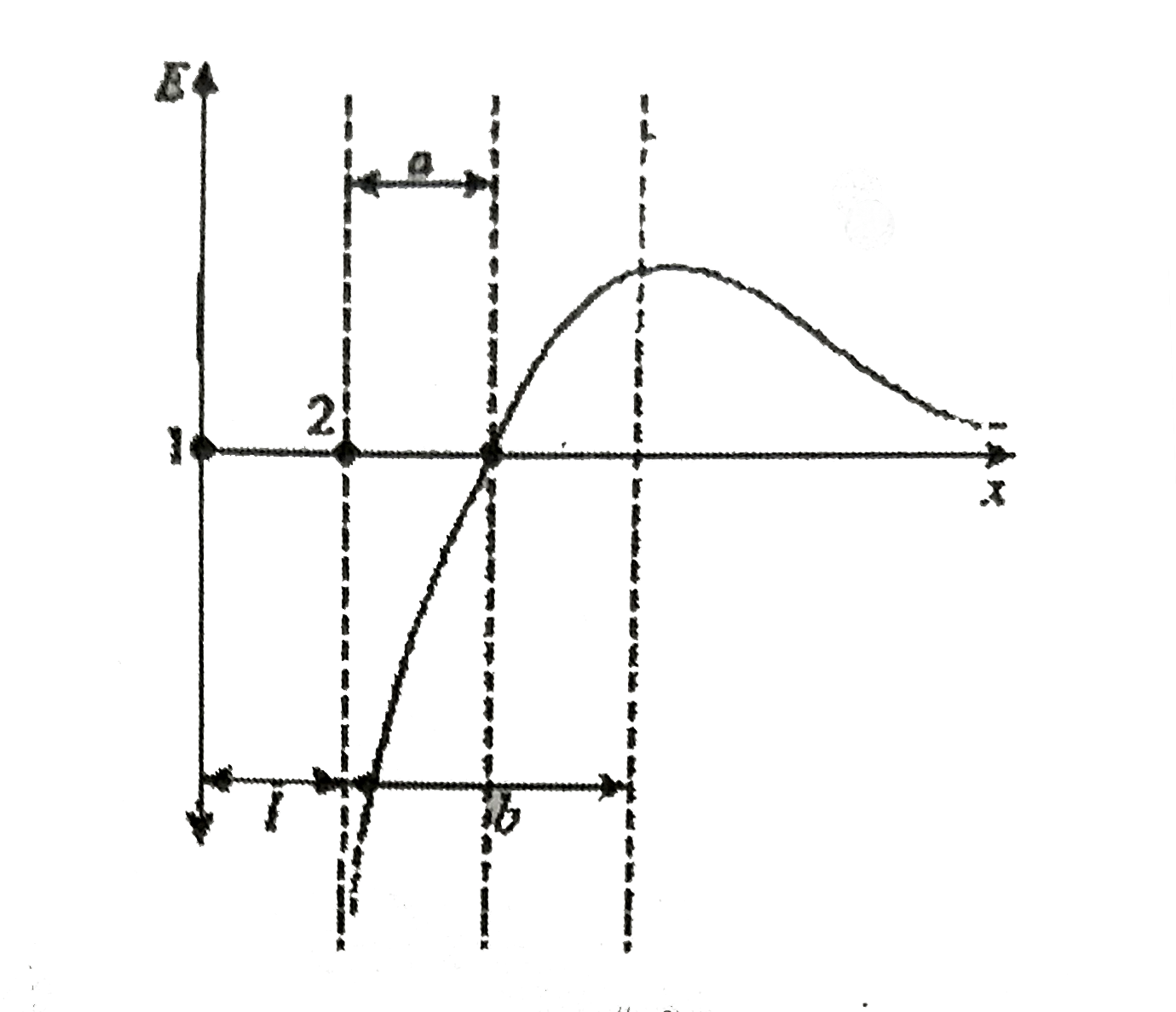
Two point charge and are positional at point A and B. The field strength to the right of charge on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is .
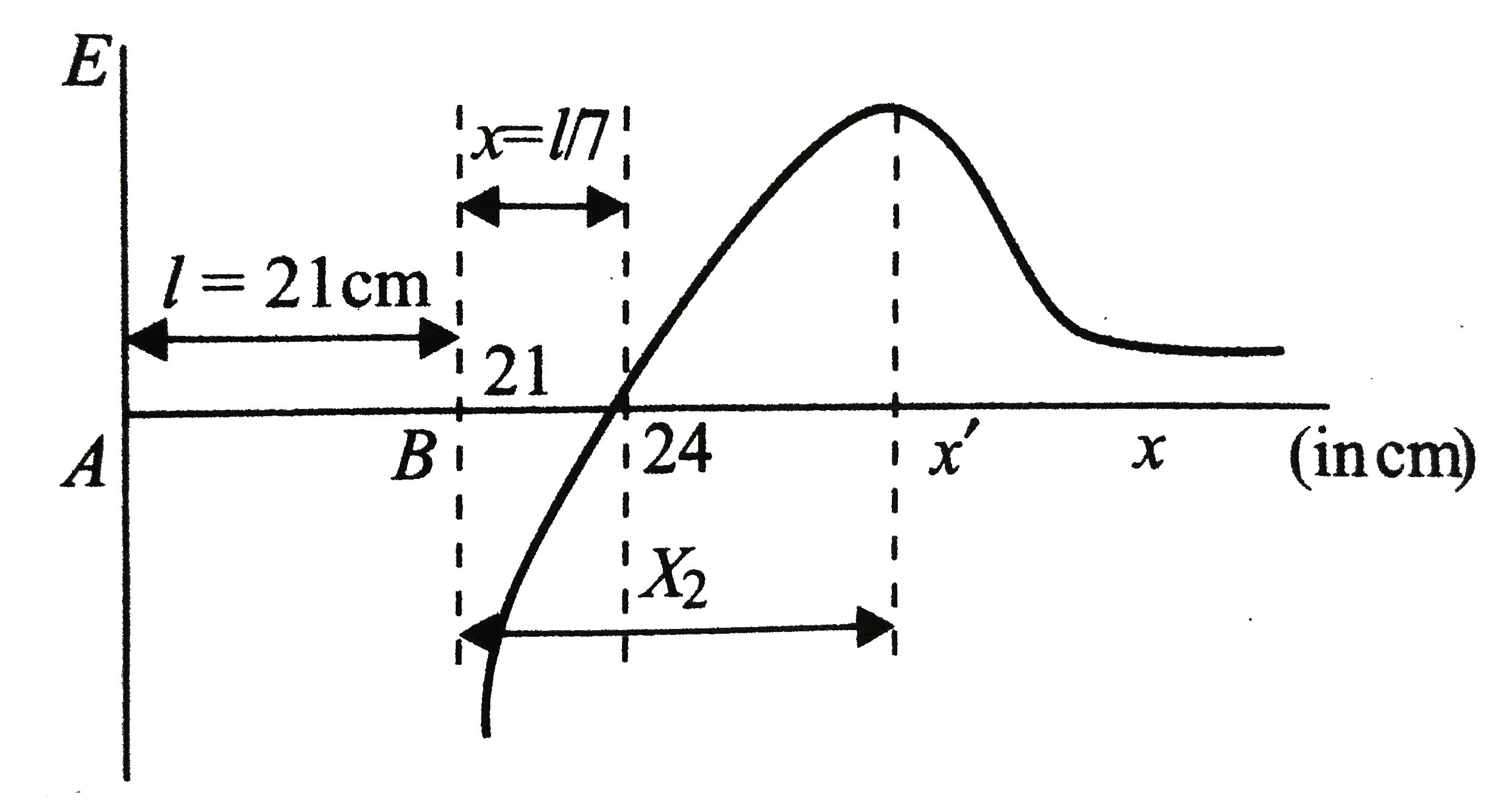
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge and .
(c ) Find the coordinate x of the point where the field strength is maximum.
The correct Answer is:A
Electric field at (2) tends to , hence the charge at (2) should be negative. There is a neutral point to the right of charges. This is possible onlu when the charge at (1) should be positive. Hence is positive and is negative. At netural point, .
or
Electric field at any position to the right of charges is
For the maximum value of E,
or or
or, or
or .
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type
20 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
Two concentric rings, one of radius a and the other of radius b, have the charges +q, and −(2/5)−3/2q, respectively as shown in fig.
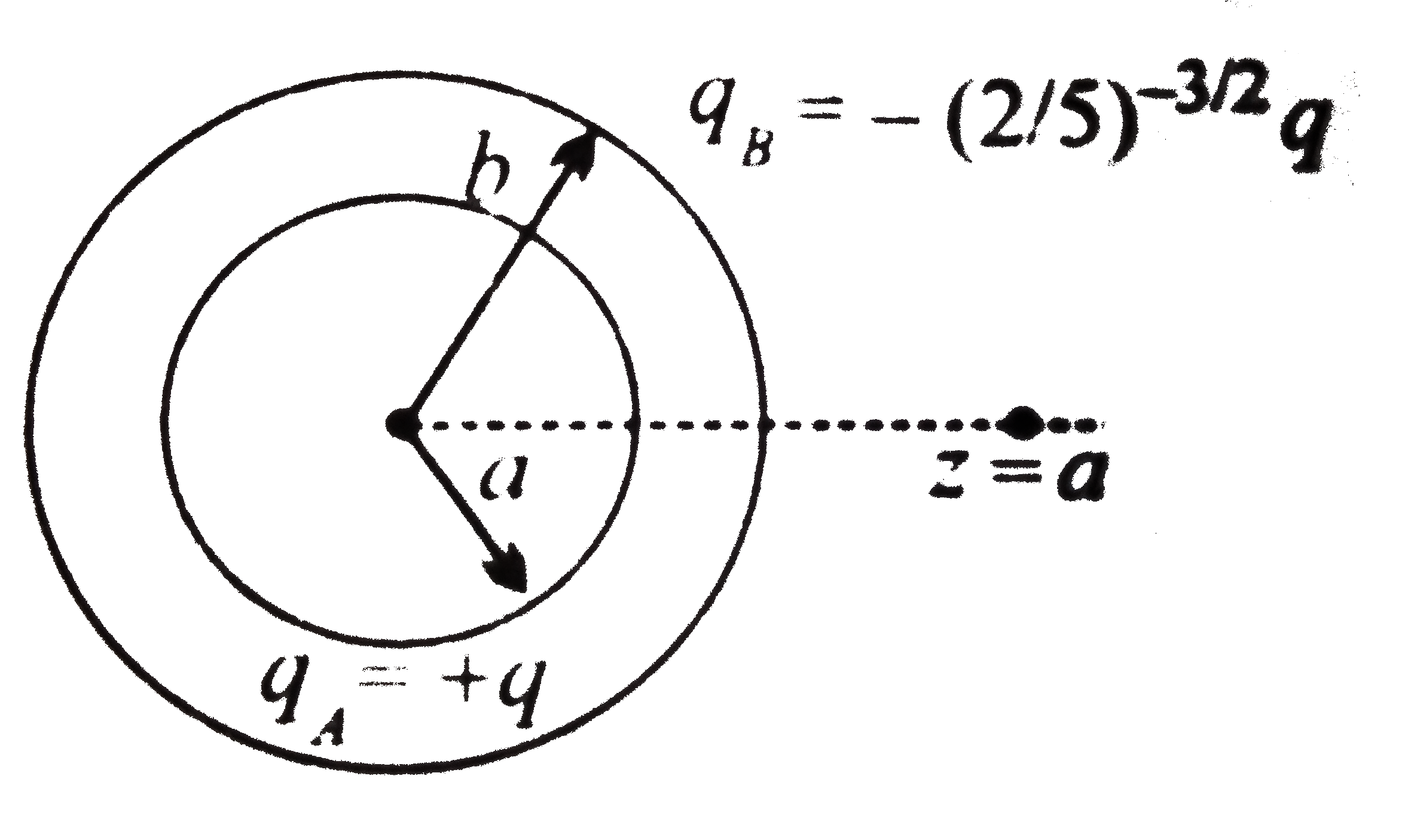
Find the ratio b/a if a charge particle placed on the axis at z =a is in equilibrium.
View SolutionA positively charged insulator is brought near(but does not touch) two metallic sphere that are in contact. The metallic spheres are then separated. The sphere which was initially farthest from the insulator will have:
View SolutionIn the arrangement shown in fig. two positive charges, +Q each,are fixed. Mark the correct statement(s) regarding a third charged particle q palce at the midpoint P that can be displaced along or perpendicular to the line connecting the charges.

View SolutionThe maximum and minimum amplitudes of a modulated wave are 15V and 5V, respectively. Find the amplitude (in volt) of the modulating wave.
View SolutionThe current (in ampere) through a copper wire having cross sectional area 2mm2 Given:
E=8.5×10−3Vm
ρ=1.7×10−8ohmm
View SolutionThe field lines for two point charges shown in fig.

(i) Is the field uniform?
(ii) Determine the ratio qA/qB.
(iii) What are the sign of qA and qB ?
(iv) Apart from infinity, where is the neutral point?
(v) If qA and qBare separated by a distance 10(√2−1) cm, find the position of neutral point.
(vi) where will the lines meet which are coming from A and are not meeting at qB?
(vii) Will a positive charge follow the line of force if free to move?
View SolutionTwo point charge Q_(a) and Q_(b) are positional at point A and B. The field strenght to the right of charge Q_(b) on the line that passes therough the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincedes with the positive direction of the x-axis. The distance between the charges is l=21 cm . (a) Find the sign of the charges. (b) Find the ration between the absolute value of charge Q_(a) and Q_(b) . (c ) Find the coordinate x of the point where the field strenght is maximum.
View SolutionIn figure two positive charges q2 and q1 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x−aξs if a positive charge Q is added at (x,0) the force on q1
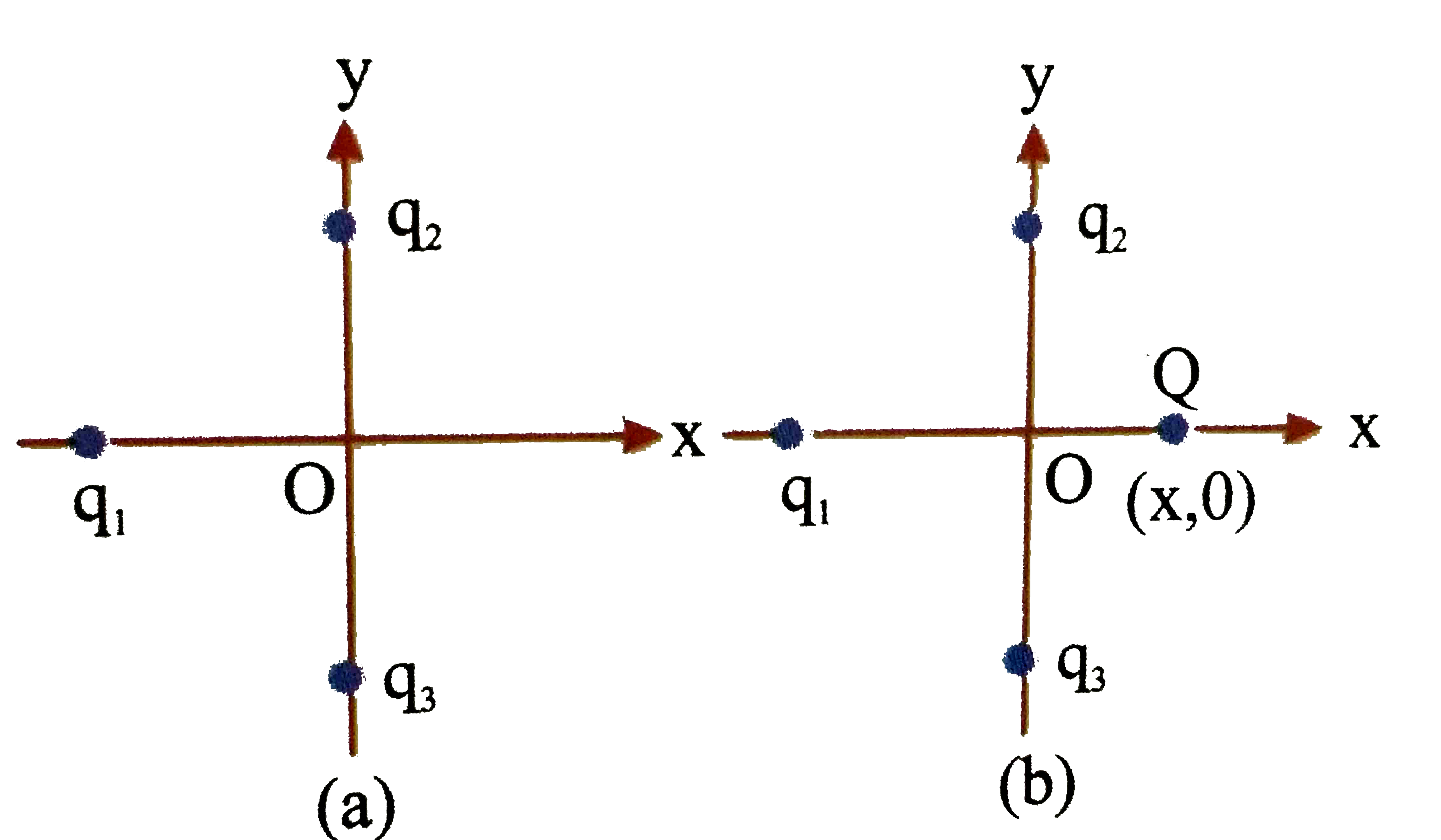
View SolutionWhen two point charges qA and qB are placed at some separation on positive x-axis at points (xA,0) and (xB,0). Given that |qA| and |qB| and xB>xA. If null point is the point where net electric field due to both the charges is zero, then
View SolutionTwo point-like charges a and b whose strengths are equal in absolute value are positioned at a certain distance from each other. Assuming the field strength is positive in the direction coinciding with the positive direction of the r axis, determine the signs of the charges for each distribution of the field strength between the charges shown in Figures (a), (b), (c), and (d).
View SolutionTwo point charges Q1 and Q2 are positioned at points I and 2. The field intensity to the right of the charge Q2 on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges ∣∣∣Q1Q2∣∣∣
(c) Find the value of b where the field intensity is maximum
[(a) Q2 is negative and Q1 is positive (b) (l+aa)2, (c) l(l+aa)2/3−1⎤⎥ ⎥ ⎥⎦
View SolutionTwo concentric conducting thin spherical shells A andB having radii rA and r8 (r_(8) gt r_(A)) are charged to Q_(A) and - Q_(B)(|Q_(B)| gt |Q_(A)|) . The electric field strength along a line passing through the centre varies with the distance x as :
View SolutionA positive point charge q_(1) is placed at (a,0) and another positive point charge q_(2) is placed at (0,a) . Find the force acting on q_(1) .
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis, exert a net electric force in the +x-direction on a charge q1 fixed along the x-axis. If a positive charge Q is added at (x,0), the force on q1.
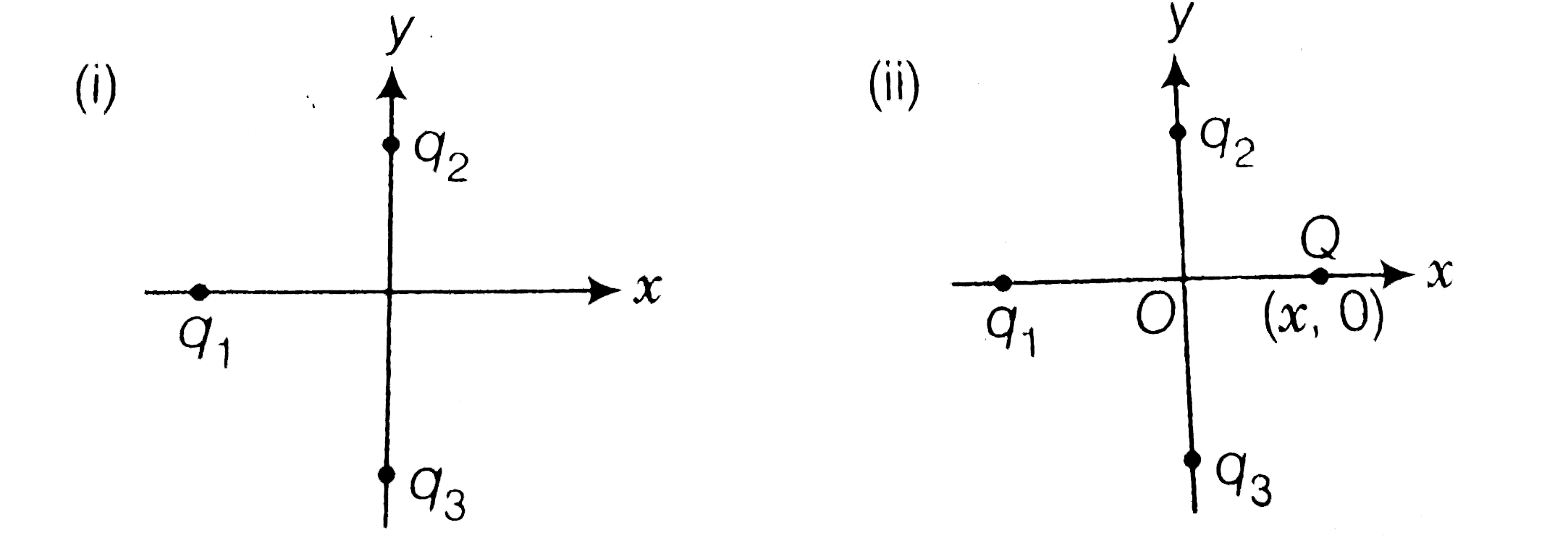
View SolutionThe following pictures depict electric field lines for various charge configurations.

(i) In figure (a) identify the signs of two charges and find the ratio ∣∣∣q1q2∣∣∣
(ii) In figure (b) calculate the ratio of two positive charges and identify teh strength of the electric field at three points A, B and C
(iii) Figure (c) represents the electric field lines for three charges . If q2 =-20nC then calculate the values of q1 and q3
View SolutionTwo points like charges QA and QB are positioned at points a and B (see figure). The electric field strength to the right of charge QB on the line that passes through the two charges varies according to a law that is represented schematically in Figure below accompaanying the problem without employing a definite scale. Assume electric field to be positive if its direct ion coincides with (the positive direction on the x-axis. THe distance between the charges is l.
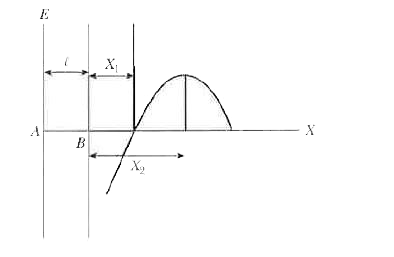

View Solution
