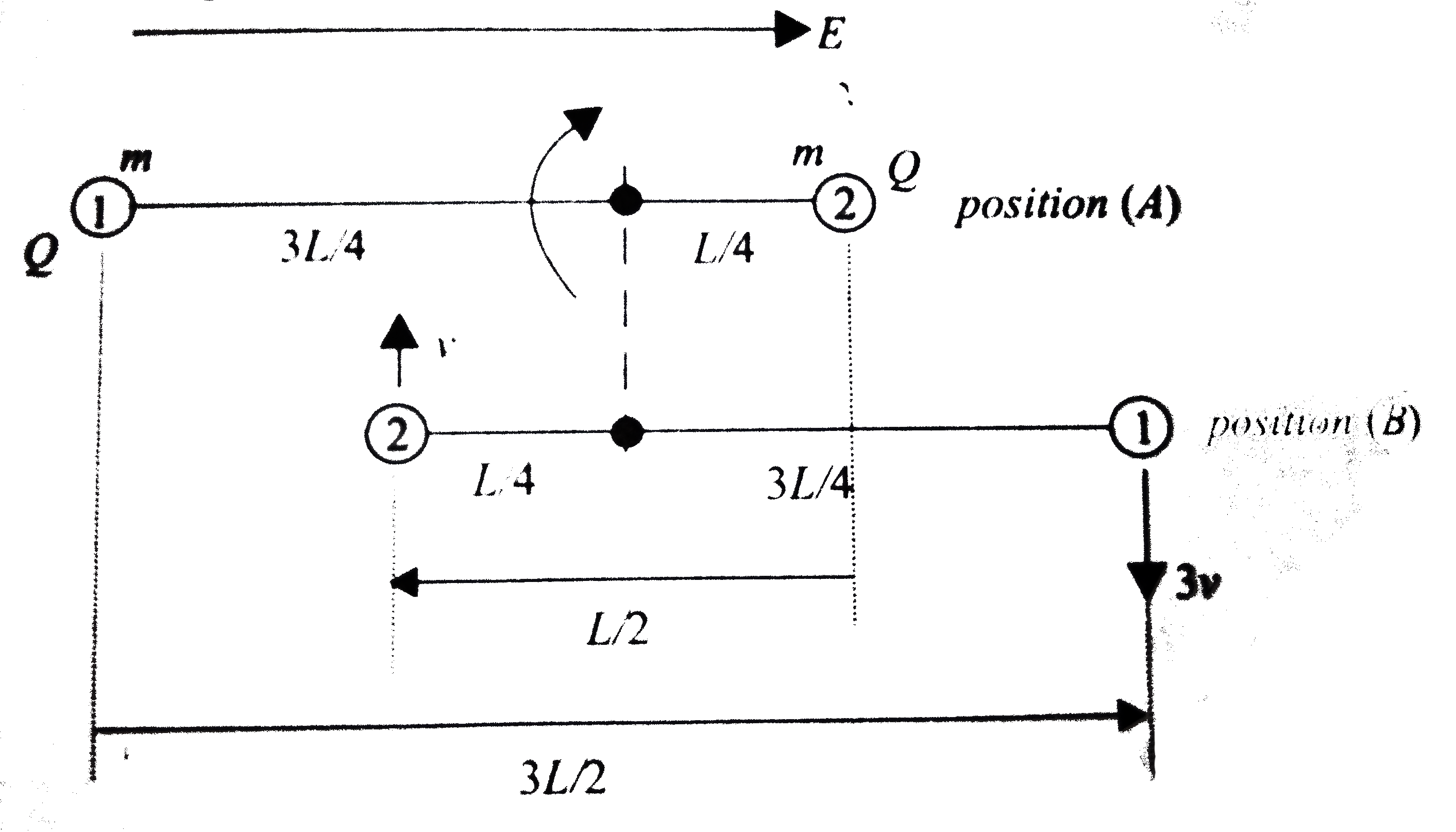
There is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it ata distance L/4 from one of its ends.
At first the rod is in unstabel equilbrium in a gorizontal umifrom electric field of field strenght E. Then we gently displace it from this position. Determine the maximim velocity attained by the ball taht is closer to the axis in the subsequent motion
√2QELm
√2QEL5m
√QEL5m
√4QEL5m
The correct Answer is:C
Position (A) is of unstable equilibrium, because if displaced from this postion, resultanat torque will be in the direction of displacement and finally it will attain equilibrium position(B). At positions (B), velocity will be maximum.
W=ΔKE
or, QE3L2−QEL2=12m[v2+(3v)2]
or, v=√QEL5m
Now we will find time period.
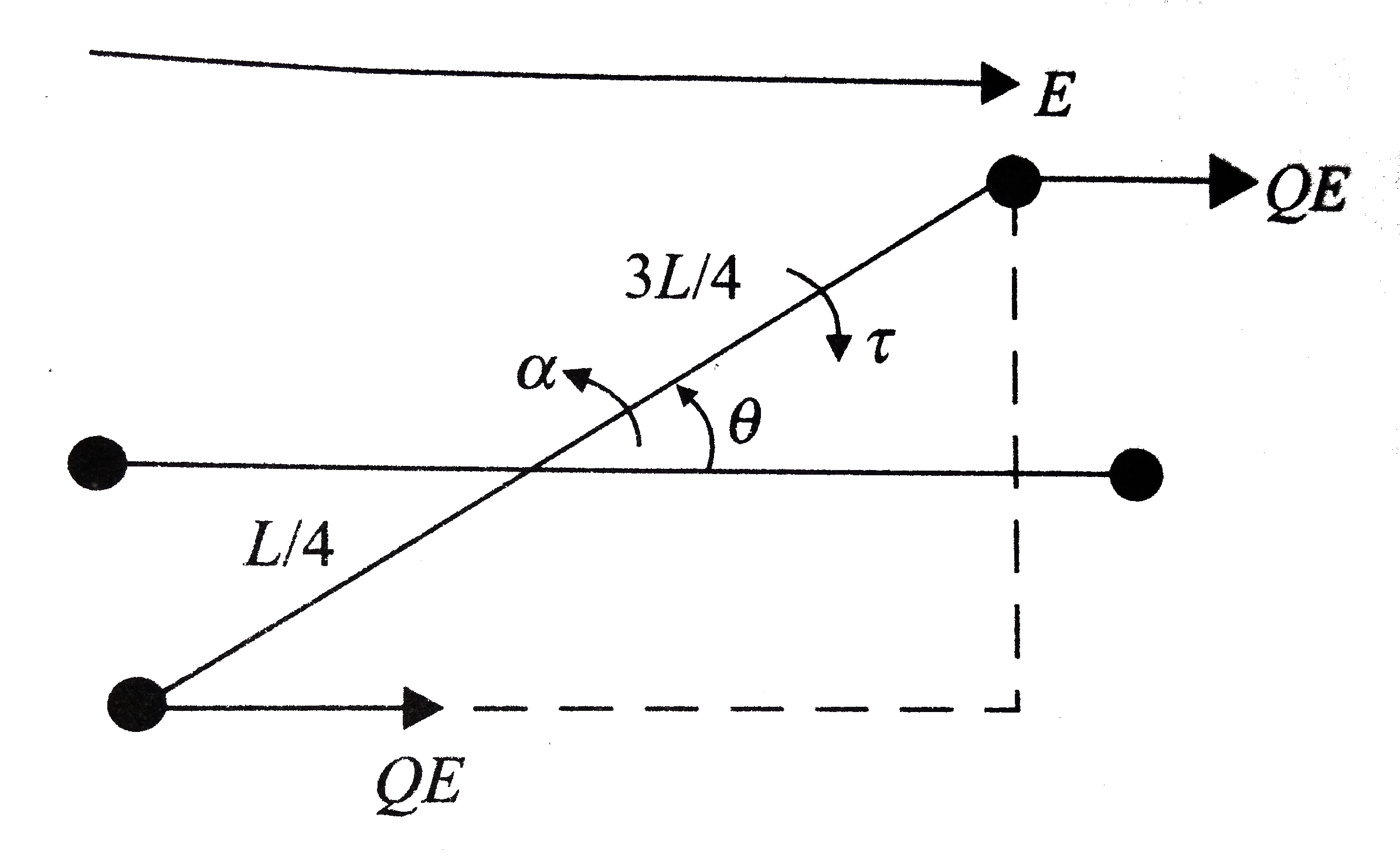
τ=QE3L4sinθ−QEL4sinθ=−Iα
or QEL2sinθ=−m[(L4)2+(3L4)2]α
or QEL2θ=−10mL216α or α=−(45QEmL)θ
ω2=4QE5mLorω√4QE5mL
T=2πω=2π√5mL4QE.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type
20 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
A massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance L4 from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle Δθ from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m.
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View Solution
Knowledge Check
There is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it ata distance L/4 from one of its ends.
What is the time period of the SHM as mentioned in the above question?A2π√mLQEB2π√2mL3QEC2π√5mL8QED2π√5mL4QEThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a L/4 distance from one of its ends.
What is the time period of the SHM as mentioned in previous question?A2π√mLQEB2π√2mL3QEC2π√5mLQED2π√5mL4QEThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a L/4 distance from one of its ends.
In what position is the rod to be set so that if displaced a little from that position it begins a hormonic oscillation about the axisA?A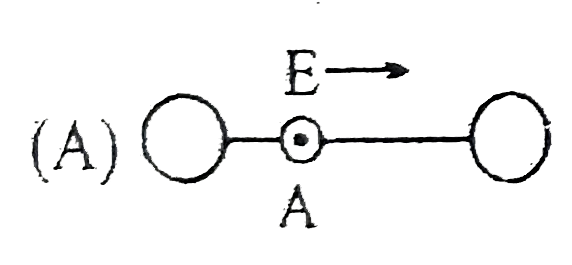 B
B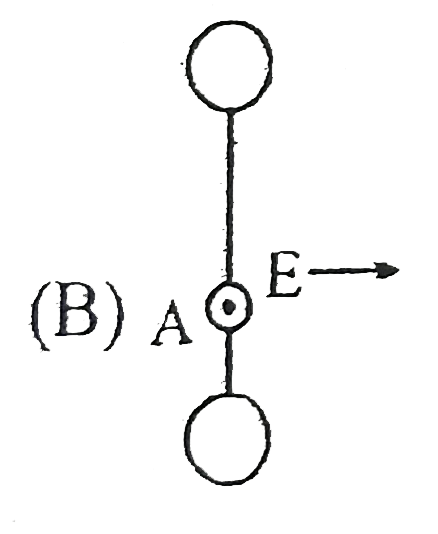 C
C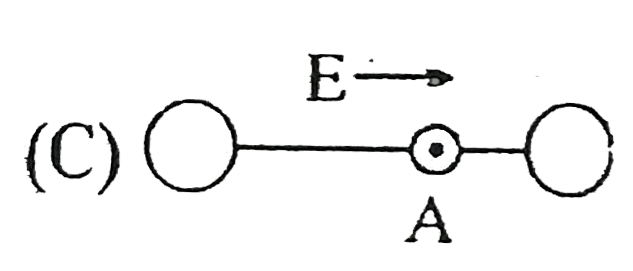 D
D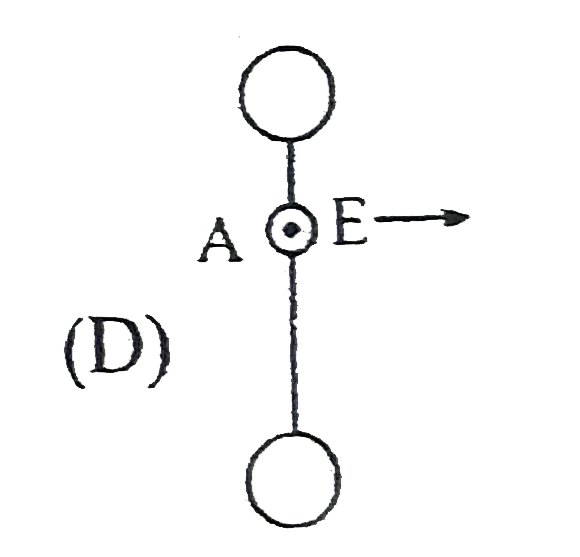
The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
