A cube of side a and mass on just floats on the surface of water as shown in the figure. The surface tension and density of water are T and ρw respectively. If angle of contact between cube and water surface is zero, find the distance h (in metres) between the lower face of cube and surface of the water.
(Take m=1kg,g=10ms−12,aT=104 unit and ρwa2g=10 unit)

The correct Answer is:2
Mg+FST=B
mg+4aT=a2hρwg

10+4×104=10h
h=2m
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Integer
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Fill In The Blanks
Explore 1 Video
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
_E01_235_Q01.png)
A cube with mass m completely wettable by water floats on the surface of water each side of the cube is a what is the distance h between the lower face of cube and the surface of the water if surafce tension is S. Take densities of water as ρw take angle of contact is zero.
View SolutionA cube of mass m=800g floats on the suface of water. Water wets it completely. The cube is 10cm on each edge. By what additional distance is it buoyed up or down by surface tension? Surface tension of water =0.07Nm−1
View Solution
Knowledge Check
A cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
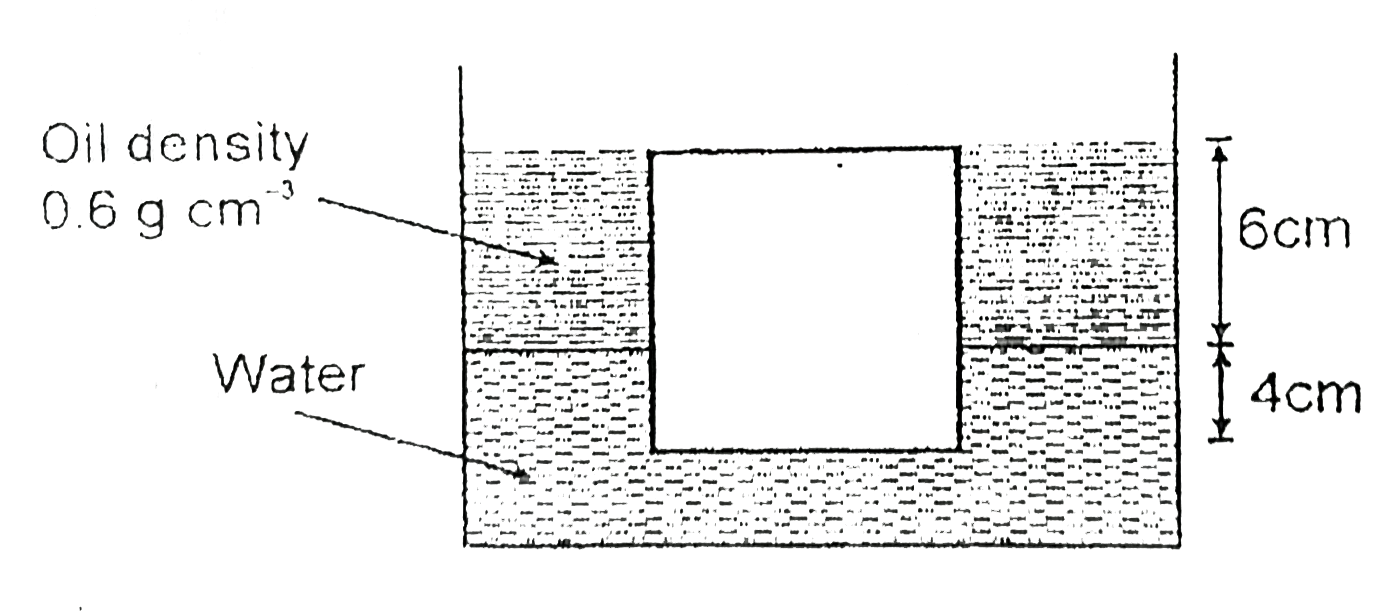 A706gB607gC760gD670g
A706gB607gC760gD670gA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is
 A200PaB620PaC900PaD800Pa
A200PaB620PaC900PaD800PaA cube with a mass =20g wettable water floats on the surface of water. Each face of the cube is α=3cm long. Surface tension of water is 70dyn/cm. The distance of the lower face of the cube from the surface of water is (g=980cms−12)
A2.3cmB4.6cmC9.7cmD12.7cm
An annular disc of radius r1=10cm and r2=5cm is placed on a water surface. Find the surface tension force on the disc if we want to pull it from water surface. Take coefficient of surface tension as σ=7×10−3N/m,g=10ms−12.

View SolutionThe velocity of water in a river is 2ms at the surface.If the river is 2m deep the shearing stress between the horizontal layers of water assuming bottom layer at rest (η=10−3SI units for water)
View SolutionA long capillary tube of radius 0.2mm is placed vertically inside a beaker of water.
If the surface tension of water is 7.2×10−2N/m the angle of contact between glass and water is zero, then determine the height of the water column in the tube.
View SolutionCalculate the tension in the string shown in the figure. All the surfaces are frictionless. (Take g=10/ms−1)
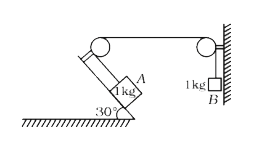
View SolutionA solid block of mass 2kg is resting inside a cube shown in figure The cube is moving with a velocity ˆv=5ˆi+2ˆjms−1 If the coefficient of friction between the surface of cube and block is 0.2 then the force of friction between the block and cube is

View Solution

