On gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress proportional to strain or, Stressstrain = a constant for the material of wire.
Just on crossing the yield region, the material will have

reduced stress
increased stress
breaking stress
constant stress
The correct Answer is:A, C
On crossing the yield region, the material will experience the breaking stress and further elongation causes reduction in stress and break of the wire. So,options a and c are correct.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Integer
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Fill In The Blanks
Explore 1 Video
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
Knowledge Check
On gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress prop strain or, Stressstrain = a constant for the material of wire.
Just on crossing the yield region, the material will have Aincreased and breaking stressBreduced and breaking stressCconstant stressDNone of these
Aincreased and breaking stressBreduced and breaking stressCconstant stressDNone of theseOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress ∝ strain or, Stressstrain = a constant for the material of wire.
Two wires of same material have length and radius (L,r) and (2L,r2). The ratio of their young's modulii is
 A1:2B2:3C2:1D1:1
A1:2B2:3C2:1D1:1Within the elastic limit, stress is directly proportional to strain produced in a body is the statement of
ARobert's lawBHooke's lawCNewton's lawDBoyle's law
Figure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
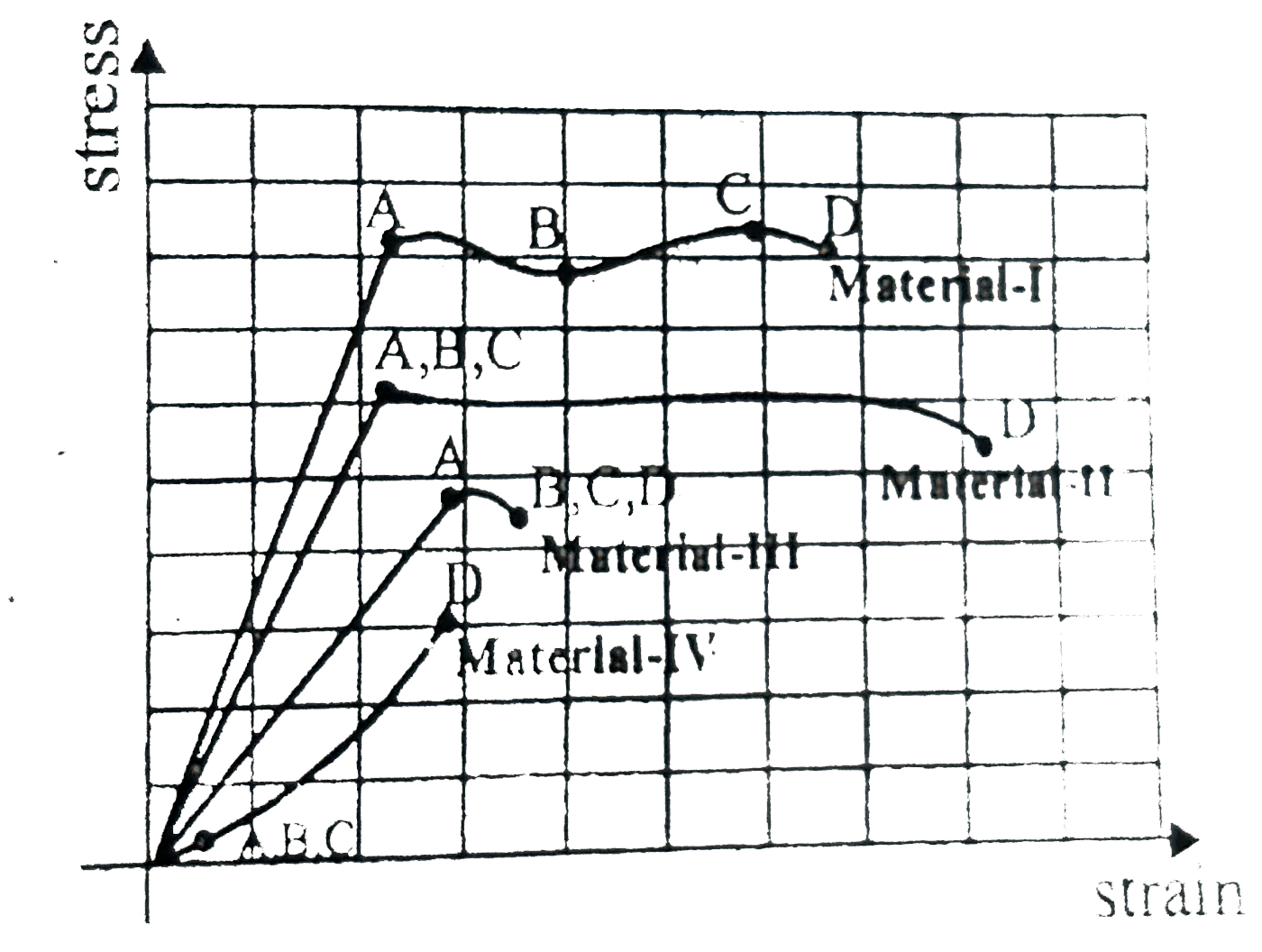
Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
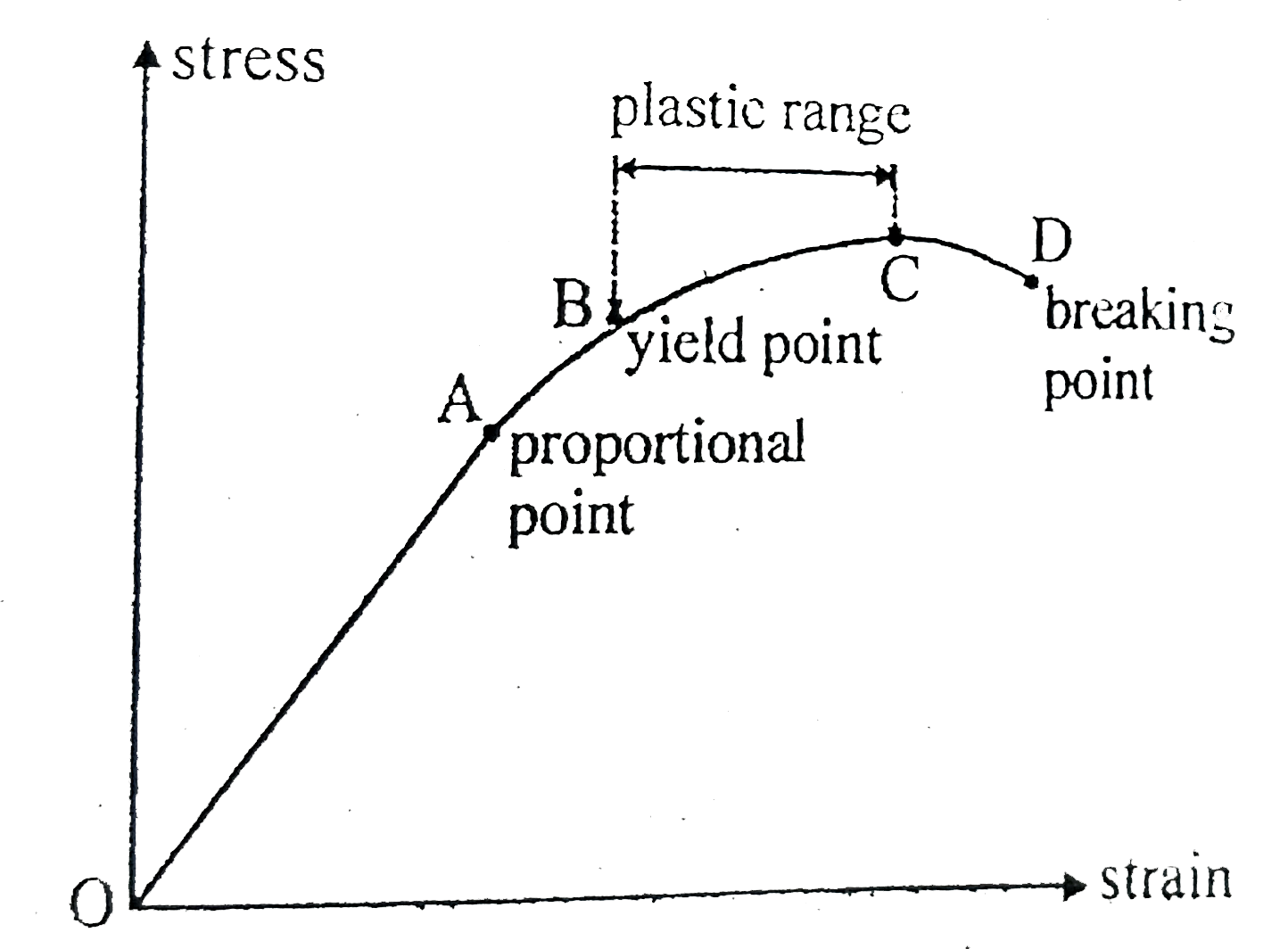
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
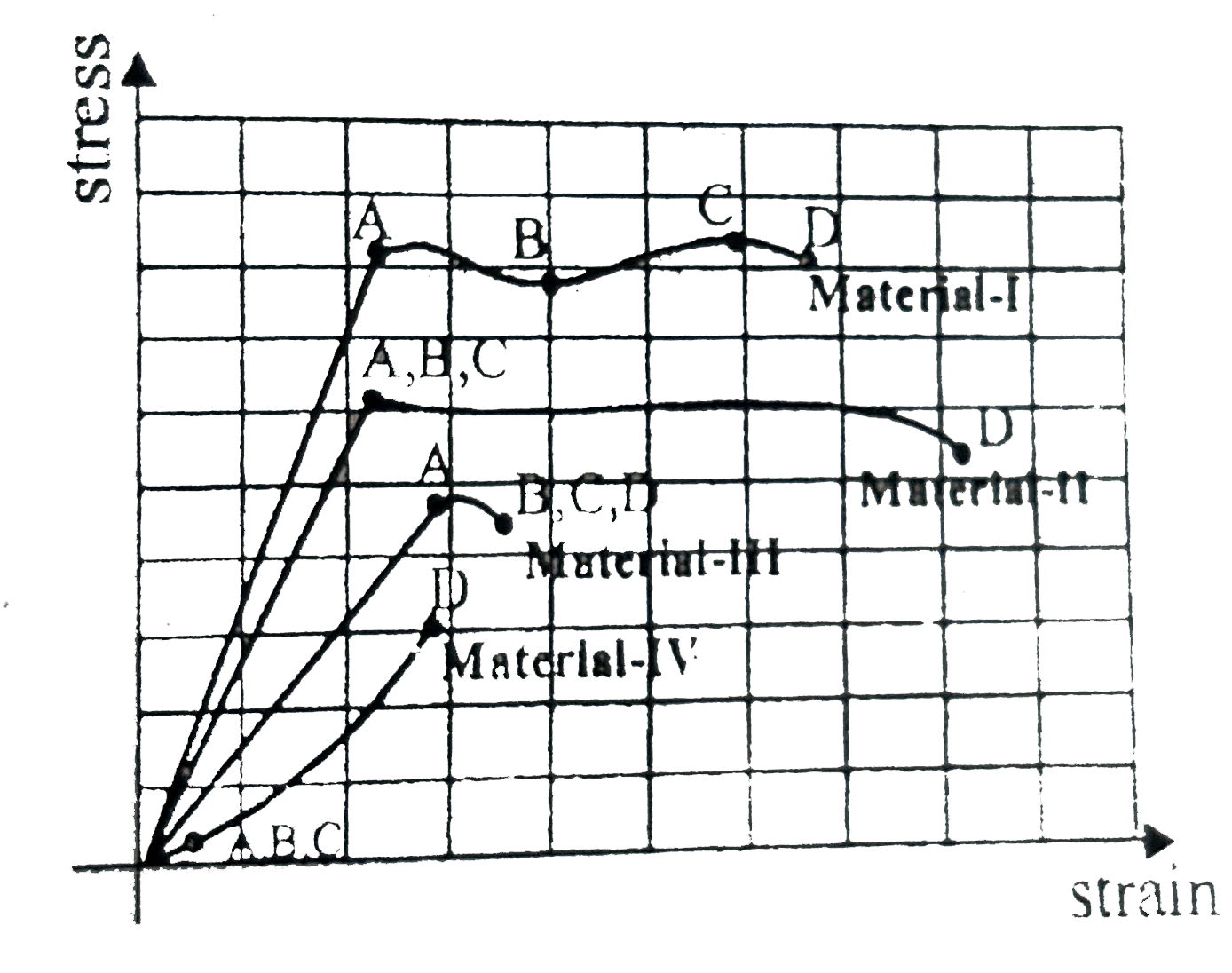
Material which is most brittle is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
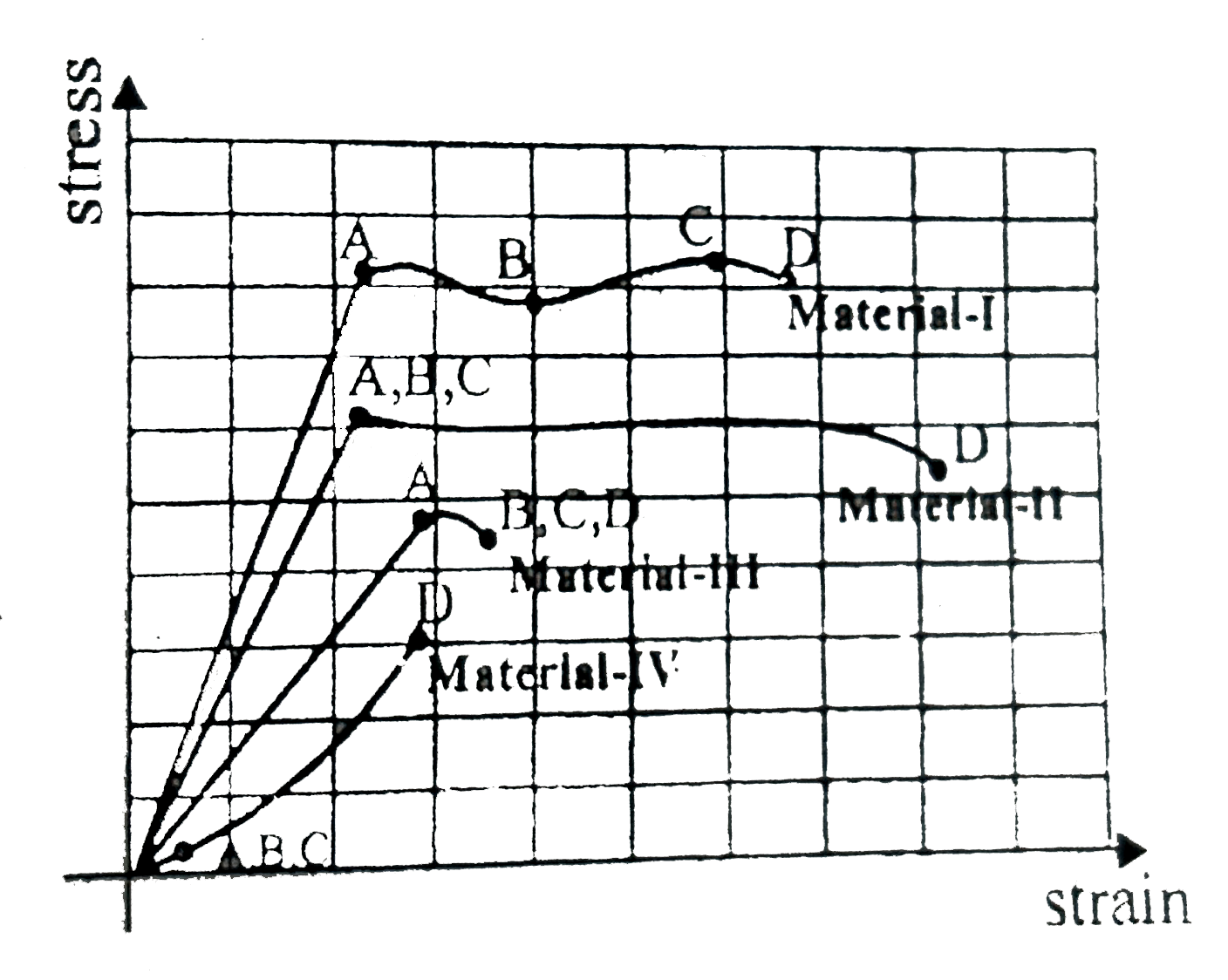
If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFor a steel wire, stress is directly proportional to strain. This is possible only when
View SolutionThe stress- strain graphs for materials A and B are as shown. Choose the correct alternative
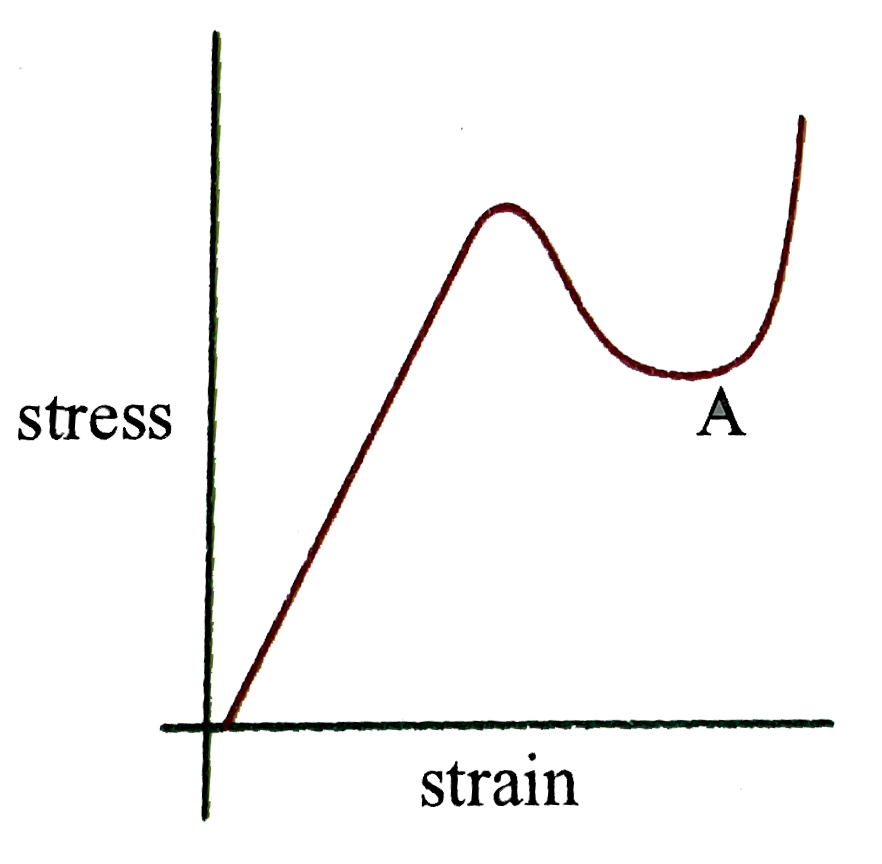
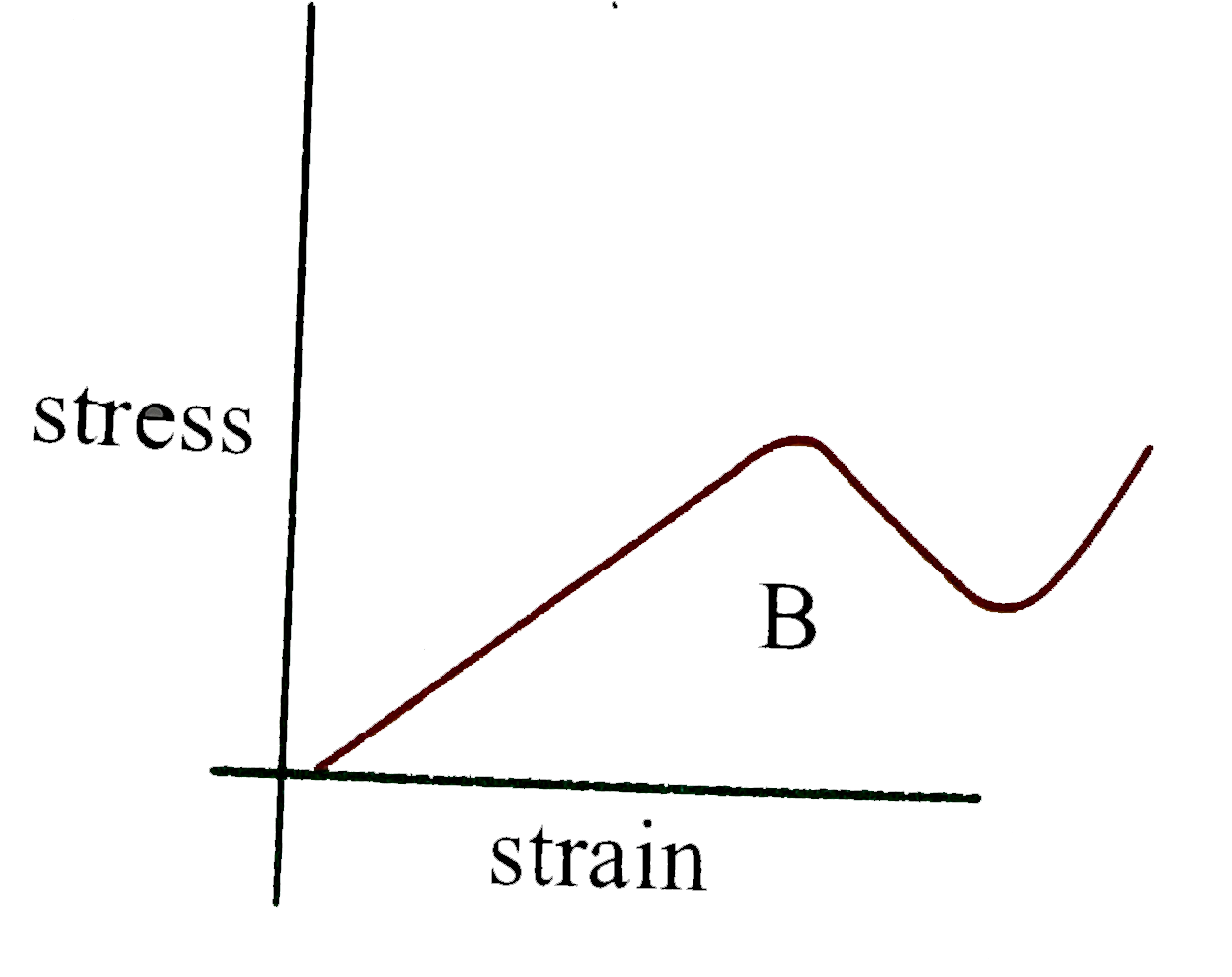
View Solution

