A uniform rod of length L and density ρ is being pulled along a smooth floor with a horizontal acceleration α (see Fig.) The magnitude of the stress at the transverse cross-section through the mid-point of the rod is……..
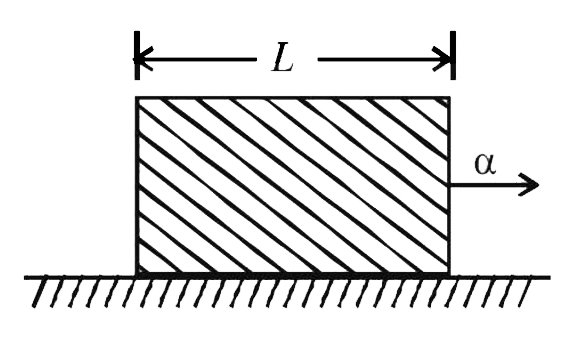
Let A be area of cross section of the rod.
Mass m×volume×density=(L2A)ρ
T=−ma=(L2Aρa)
Therefore stress TA=12ρaL
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:SCQ_TYPE
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:LC_TYPE
Explore 3 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Integer
Explore 6 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
[M.I. of the rod about A is ML23]
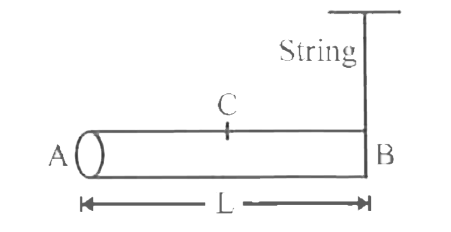
View Solution
Knowledge Check
A uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
Aits center of mass moves vertically downwards on a straight lineBIts center of mass remains in restCthe rod rotates about a vertical axisDBoth a and c are correctA uniform rope of length 'L and linear density 'μ' is on a smooth horizontal table with a length 'I' lying on the table. The wrok done in pulling the hanging part on to the table is
Aμg(L−l)22Bμg(L−l)22l2Cμg(L−l)22L2DμgL2(L−l)A uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elastic potential energy stored in section PQ and section QR of the rod isA19:37B21:39C23:41D17:35
A uniform rod of length L and mass M has been placed on a rough horizontal surface. The horizontal force F applied on the rod is such that the rod is just in the state of rest. If the coefficient of friction varies according to the relation μ =Kx where K is a +ve constant. Then the tension at mid point of rod is?
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
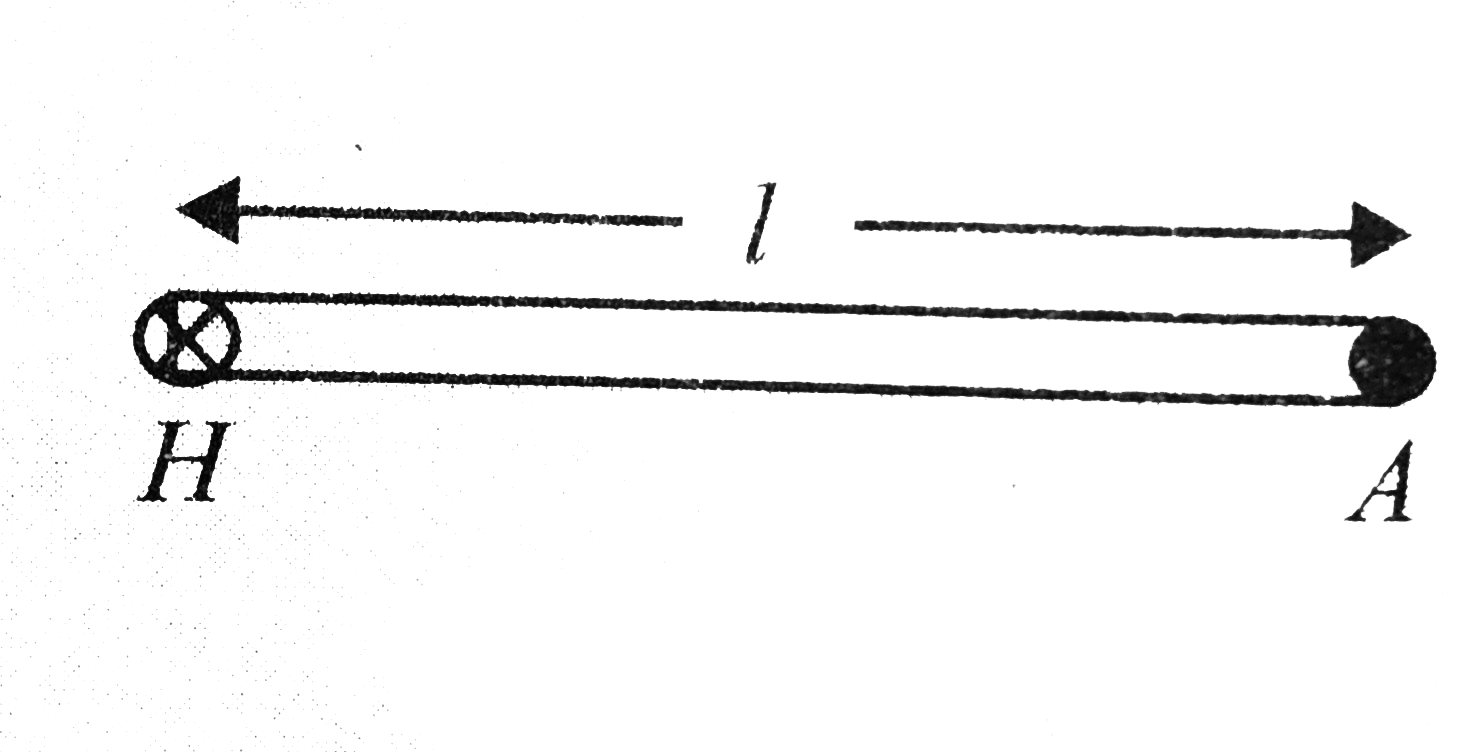
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elongation in section PQ of rod and section QR of rod is
View Solution

