A long capillary tube of radius 0.2mm is placed vertically inside a beaker of water.
If the tube is now pushed into water so that only 5.0cm of its length is above the surface, then determine the angle of contact between the liquid and glass surface.
cos−1(45)
cos−1(57)
cos−1(35)
cos−1(54)
The correct Answer is:B
Here s=7.0x10−2N/m,r=0.2×10−3m,r=103kg/m3
we know that the hieght of liquid in the tube is
h=2σcosθ/ρRg
where R is the radius of the menisus, and θ is the angle of contact.
Since θ=0 (given), radius of the meniscus is equal to the radius of the capillary tube i.e. R=r
∴h=2(7.0×10−2)(103)(0.2×10−3)(10)=0.07m
or h=7.0cm
When the length of the capillary tube above the free surface of the liquid is less than the height of liquid that rise in the tube, radius R of the free surface is not equal to the radius of the tube. It is greater than r as the surface tennis to be flatter.
According to the equation p1−p2=(4σ/R), the pressure difference across te surface is given by
△p=2σcosθR
If p1 and p2 are the pressure just above and below the mensisus, respectively then p1−p2=ρgh0
∴ρgh0=2σr...........i
In part a we have seen than when h0=h,θ=0,R=r, and ρgh=2σr.......ii
Therefore dividing eqn i by eqn ii we have rR=h0h
From the figure, it is clear that cosθ=rR
Therefore the angle of contact is
θ=cos−1h0h=cos−1(57)≈44∘
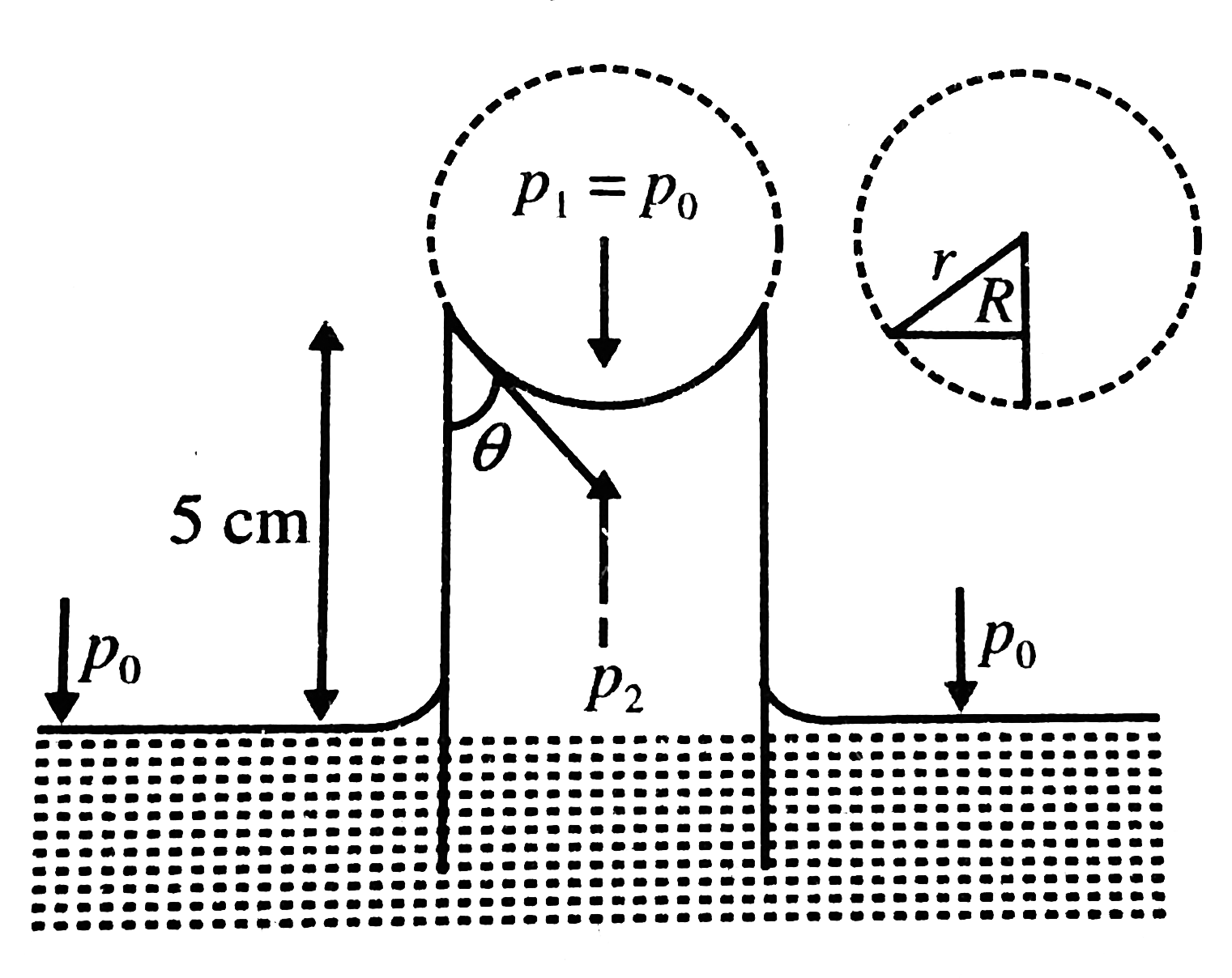
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Integer
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Fill In The Blanks
Explore 1 Video
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
A long capillary tube of radius 0.2 mm is placed vertically inside a beaker of water. Water rises to a hight of 7.05 cm in the tube making zero angle os contact. Now if tube is pushed into water so that only 5 cm of its length is above the surface, What is the new angle of contact in degrees between water and glass surface (Take √2=1.41, surface tension of water 0.07 N/m)
View SolutionA uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
View Solution
Knowledge Check
A long capillary tube of radius 0.2mm is placed vertically inside a beaker of water.
If the surface tension of water is 7.2×10−2N/m the angle of contact between glass and water is zero, then determine the height of the water column in the tube.A3cmB9cmC7cmD5cmThe lower end of a capillary tube of radius r cm is placed vertically in water. What is the heat evolved if water rise upto a height h in the capillary tube ?
Aπ2r2h2gJB−π2r2h2gJC−π2r2h2g2JDπr2h2g2JLiquid rises to a height of 2 cm in a capillary tube and the angle of contact between the solid and the liquid is zero. If the tube is depressed more now so that top of capillary is only 1 cm above the liquid, then the apparent angle of contact between the solid and the liquid is
A0∘B30∘C60∘D90∘
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
View SolutionA capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part (a), find the angle θ made by the water surface in the capillary with the wall.
View SolutionA glass capillary tube of radius r is placed vertically touching the surface of water. The water rises to height h in capillary tube. If now the tube is dipped into water till only h2 length of it is outside the water surface the , radius of curvature of the meniscus of water in capillary tube will be,
View SolutionA capillary tube of radius 0.25 mm is submerged vertically in water so that 25 mm of its length is outside water. The radius of curvature of the meniscus will be
(surface tension of water =75×10−3 N/m)
View SolutionWater rises upto 10 cm height in a long capillary tube. If this tube is immersed in water so that the height above the water surface is only 8 cm, then
View Solution

