A paper disc of radius from which a hole of radius is cut out is floating in a liquid of the surface tension . The force on the disc due to the surface tension is
The correct Answer is:D
To find the force on the paper disc due to surface tension when a hole is cut out, we can follow these steps:
1. Identify the Components:
- We have a paper disc with a radius R.
- A hole with a radius r is cut out from the disc.
- The disc is floating on a liquid with surface tension S.
2. Understand Surface Tension:
- Surface tension S acts along the length of the liquid surface in contact with the object. The force due to surface tension can be calculated using the formula:
F=S×L
where L is the total length of the perimeter in contact with the liquid.
3. Calculate the Lengths:
- The length of the perimeter of the entire disc (without the hole) is:
Ldisc=2πR
- The length of the perimeter of the hole is:
Lhole=2πr
4. Determine the Effective Length in Contact:
- Since the hole is cut out, the effective length in contact with the liquid is the circumference of the outer disc minus the circumference of the hole:
L=Ldisc−Lhole=2πR−2πr=2π(R−r)
5. Calculate the Total Force:
- The total force due to surface tension on the disc is:
F=S×L=S×(2π(R−r))
6. Final Expression:
- Thus, the force on the disc due to surface tension is:
F=S×2π(R+r)
Conclusion:
The final expression for the force on the disc due to surface tension is:
F=S×2π(R+r)
- We have a paper disc with a radius R.
- A hole with a radius r is cut out from the disc.
- The disc is floating on a liquid with surface tension S.
- Surface tension S acts along the length of the liquid surface in contact with the object. The force due to surface tension can be calculated using the formula:
F=S×L
where L is the total length of the perimeter in contact with the liquid.
- The length of the perimeter of the entire disc (without the hole) is:
Ldisc=2πR
- The length of the perimeter of the hole is:
Lhole=2πr
- Since the hole is cut out, the effective length in contact with the liquid is the circumference of the outer disc minus the circumference of the hole:
L=Ldisc−Lhole=2πR−2πr=2π(R−r)
- The total force due to surface tension on the disc is:
F=S×L=S×(2π(R−r))
- Thus, the force on the disc due to surface tension is:
F=S×2π(R+r)
The final expression for the force on the disc due to surface tension is:
F=S×2π(R+r)
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Subjective
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
A paper disc of radius R from which a hole of radius r is cut out, is floating in a liquid of surface tension, T. What will be force on the disc due to surface tension?
View SolutionA paper disc of radius R from which a hole of radius r is cut out, is floating n liquid of surface tension, T. What will be force n the disc due to surface tension?
View Solution
Knowledge Check
The force due to surface tension is
Anormal to free surfaceBnormal to free surface downwardsCalong the free surfaceDat an angle of 60∘ with free surfaceA disc of radius R has a concentric hole of radius r. It is floating on a liquid of surface tension T . What is the force of surface tension on the disc ?
A4π(R+r)TB4π(R−r)TC2π(R−r)TD2π(R+r)TFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
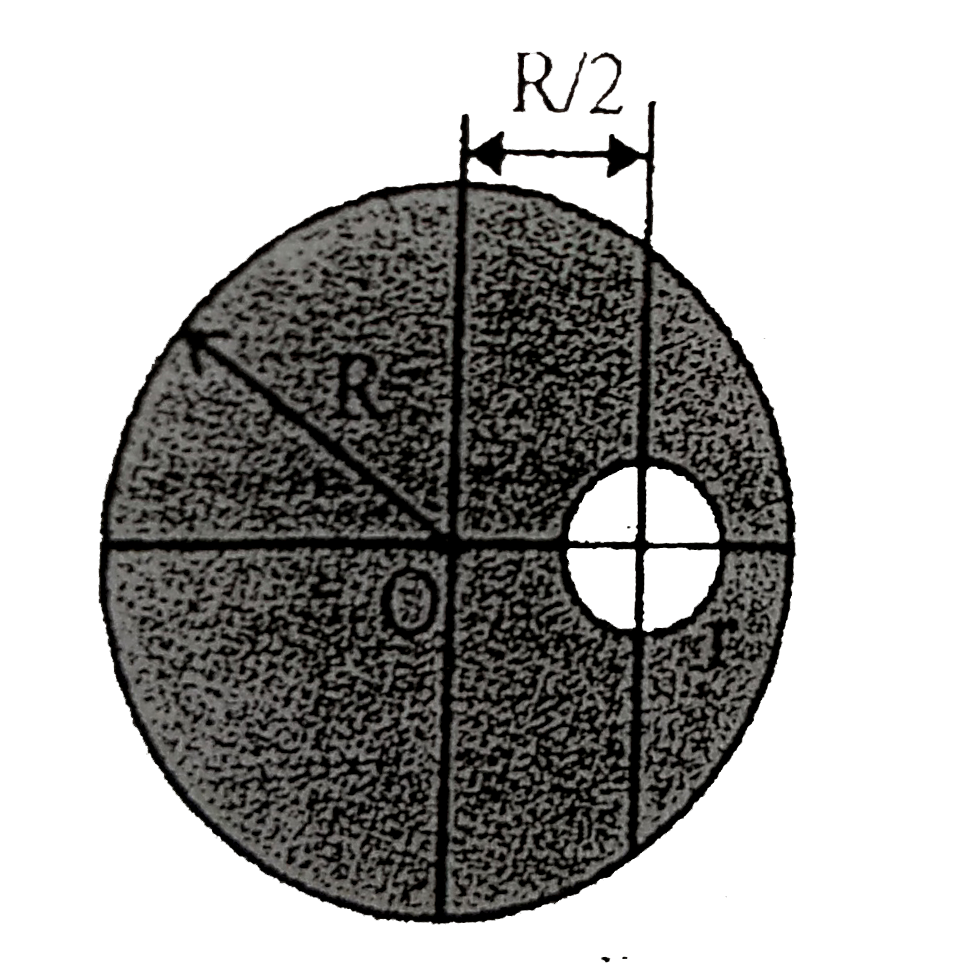 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
Figure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View SolutionA square wire frame of side / is floating on the surface of liquid of surface tension T. The force required to pull out the frame from the liquid is
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View SolutionAn annular disc of radius r1=10cm and r2=5cm is placed on a water surface. Find the surface tension force on the disc if we want to pull it from water surface. Take coefficient of surface tension as σ=7×10−3N/m,g=10ms−12.

View SolutionA disc of paper of radius R is floating on the surface of water of surface tension T . If r=20 cm and T=0.070N//m , then the force of surface tension on the disc is
View Solution

