A 5kg rod of square cross section 5cm on a side and 1m long is pulled along a smooth horizontal surface by a force applied at one end. The rod has a constant acceleration of 2ms−12. Determine the elongation in the rod. (Young's modulus of the material of the rod is 5×103N/m9).
Zero, as for elongation to be there, equal and opposite forces must act on the rod
Non-zero but cannot be determine from the give, situation
0.4μm
16μm
The correct Answer is:C
Let the force applied be p then P=ma
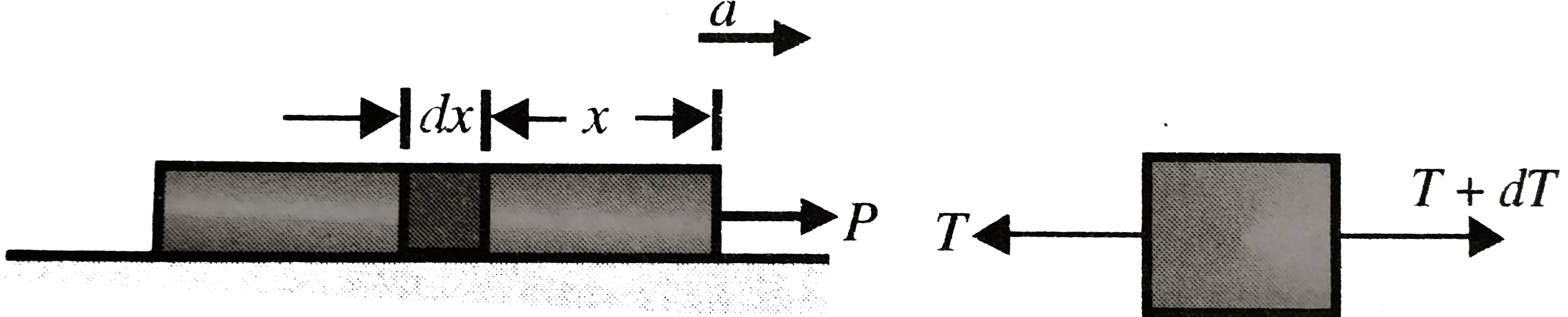
⇒p=5×2=10N
For the element shown in figure T=ml(l−x)×a
⇒⇒T=5I(1−x)×2=10(1−x)
Elongation in dx is △(dx)dX=T/AA
△(dx)=10(1−x)(5×10−2)2×15×109dx
Total elongation △l=∫1010(1−x)5×10−4×15×109dx=0.4×10−6m
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Subjective
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
View Solution
Knowledge Check
A uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elastic potential energy stored in section PQ and section QR of the rod isA19:37B21:39C23:41D17:35A uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :A7F2L6AYB11F2L6AYC5F2L6AYD3F2L2AYA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elongation in section PQ of rod and section QR of rod isA1:1B3:5C5:7D1:2
A rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

View SolutionA metallic rod of length 1m is rigidly clamped at its mid point. Longirudinal stationary wave are setup in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is 2×10−6m. Write the equation of motion of a point 2 cm from the midpoint and those of the constituent waves in the rod, (Young,s modulus of the material of the rod =2×1011Nm−2 , density =8000kg−m−3). Both ends are free.
View SolutionA rod of length l, mass M, cross section area A is placed on a rough horizonatal surface. A horizonatal force F is applied to rod as shwon in figure. The coefficient of fricition between rod and surface is μ, the Young, modulus of material of rod is Y. [Assume that fricition force is distributed uniformly on rod]

Teh elongation in rod if F>μMg is
View SolutionA rod of length l, mass M, cross section area A is placed on a rough horizonatal surface. A horizonatal force F is applied to rod as shwon in figure. The coefficient of fricition between rod and surface is μ, the Young, modulus of material of rod is Y. [Assume that fricition force is distributed uniformly on rod]
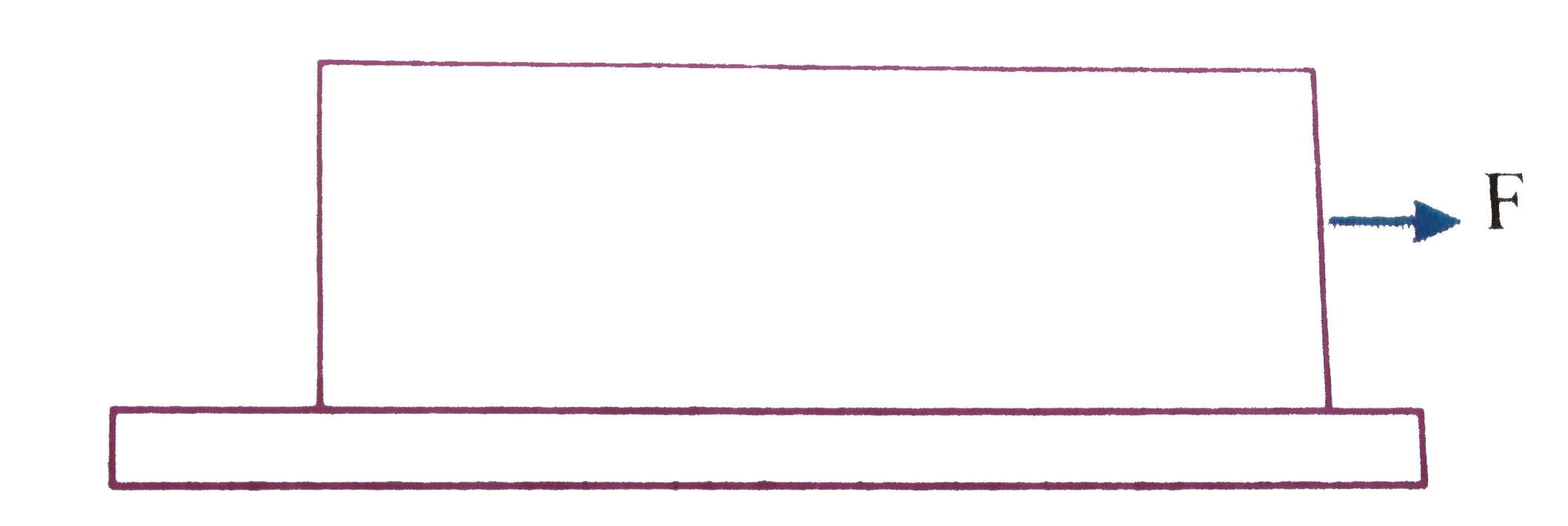
The elongation in the rod if F<μMg is
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View Solution

