A bob of mass m hangs from the ceiling of a smooth trolley car which is moving with a constant acceleration a. If young's modulus, radius and length of the string are Y,r and I, respectively, find the (a) stress in the string and (b) extension of the string when it makes a constant angle relative to vertical.

The correct Answer is:(m√g2+a2lπr2Y)
Relative to the accelerating frame (trolley car), the forces acting on the bob are as shown in the figure.
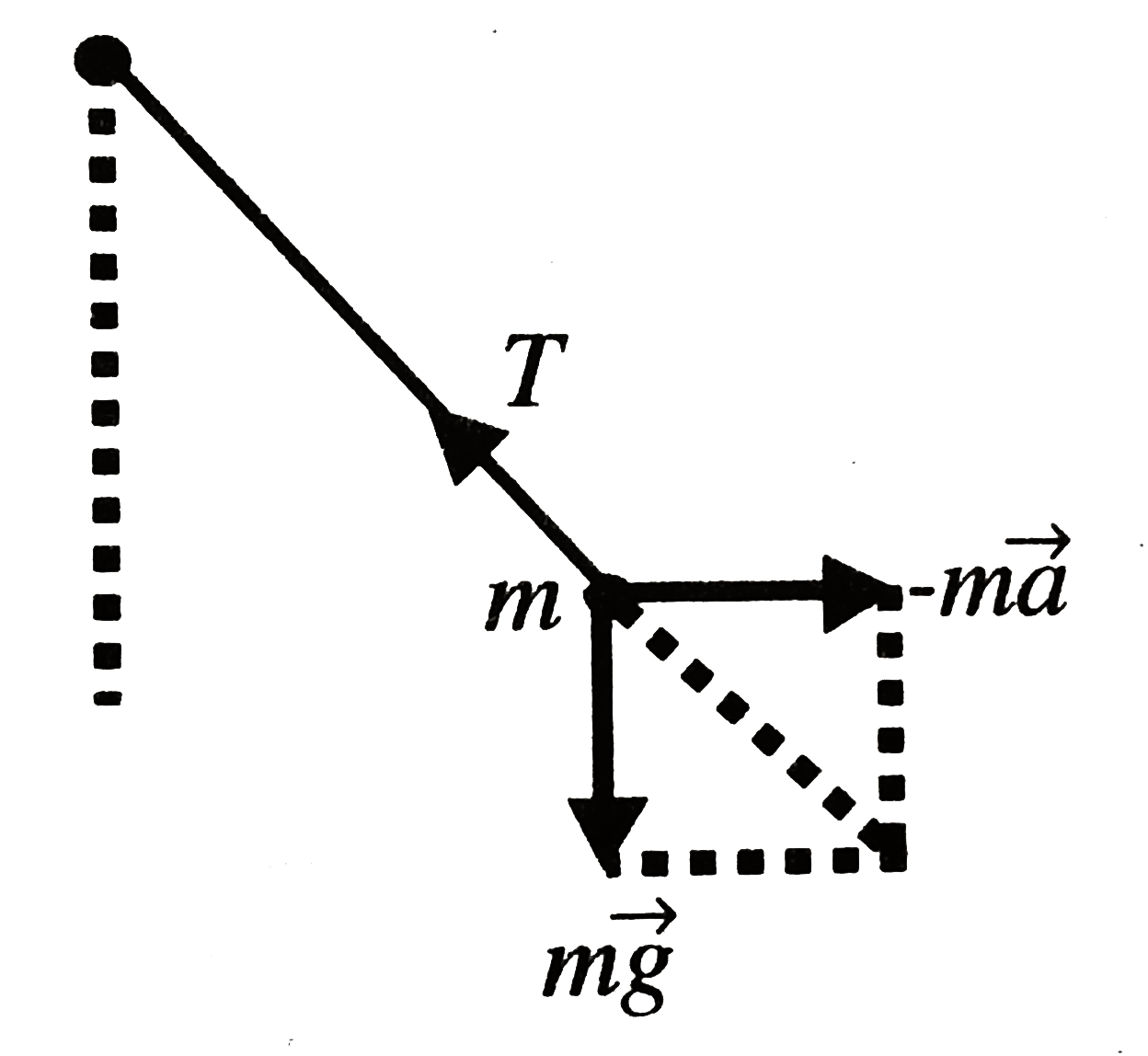
Then T=m√a2+g2 ltbr> Since the string is light, same tension is felt at all points of the string.
Putting the area of cross section of the string A=πr2 in the formula
σ=F'a
where F'=T=m√a2+g2
σ=m√g2+d2πr2
b. As Y=F/A△l/l=σl△l
which gives △l=σlY
Hence △l=m|→a−→g|lπr2=m(√g2+a2)lπr2Y
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Single Correct
Explore 112 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Exercise 5.3
Explore 9 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
A pendulum of mass m and length l is suspended from the ceiling of a trolley which has a constant acceleration a in the maximum deflection θ of the pendulum from the vertical.

View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View Solution
Knowledge Check
A small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
Atan−1(a/g) in the direction of motionBtan−1(a/g) opposite to the direction of motionCtan−1(g/a) in the direction of motionDtan−1(g/a) opposite to the direction of motionA plumb bob is hanging from the ceiling of car. If the car move with acceleration a, the angle made by the string with the vertical is
Atan−1(ag)Btan−1(ga)Ccos−1(ga)Dcos−1(ag)A pendulum of mass m hangs from a support fixed to a trolley which is moving up to the inclined plane with uniform acceleration 'a'. The angle which the string makes with vertical in equilibrium is
 A0Btan−1αCtan−1(a+gsinαgcosα)Dtan−1(acosαg+asinα)
A0Btan−1αCtan−1(a+gsinαgcosα)Dtan−1(acosαg+asinα)
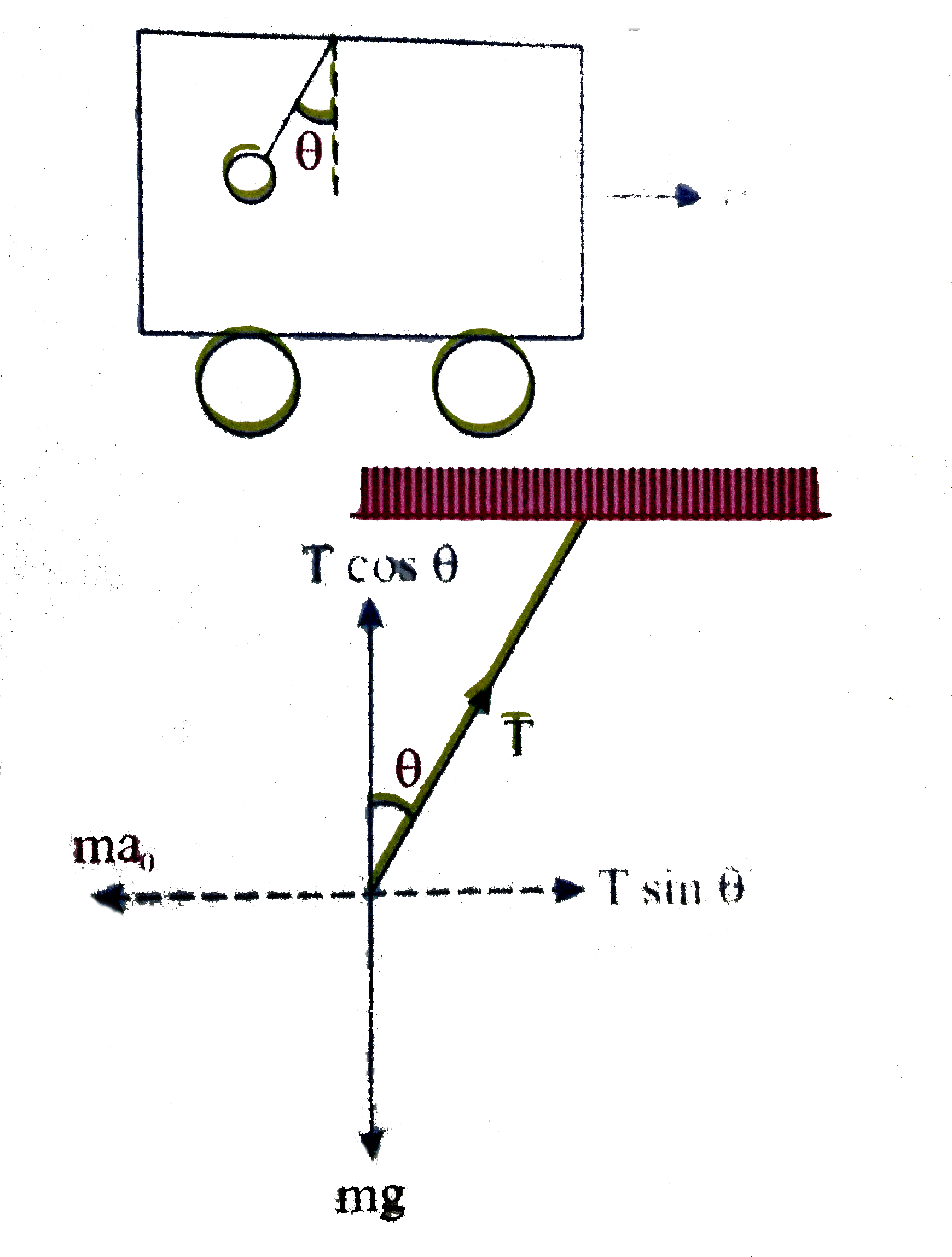
A pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Findthe angle made by the string with the vertical.
View SolutionA pedulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road Find the angle made by the string with vertical at equilibrium Also find the tension in the string in this position
 .
.
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with to the road. Find the angle made by the string with the verical and tension in the string.
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
View SolutionOne one rainy day a car starts moving with a constant acceleration of 1.2m/s2. If a toy monkey is suspended from the ceilling of the car by a string, then find the angle with the vertical with the string be now inclined.
View Solution

