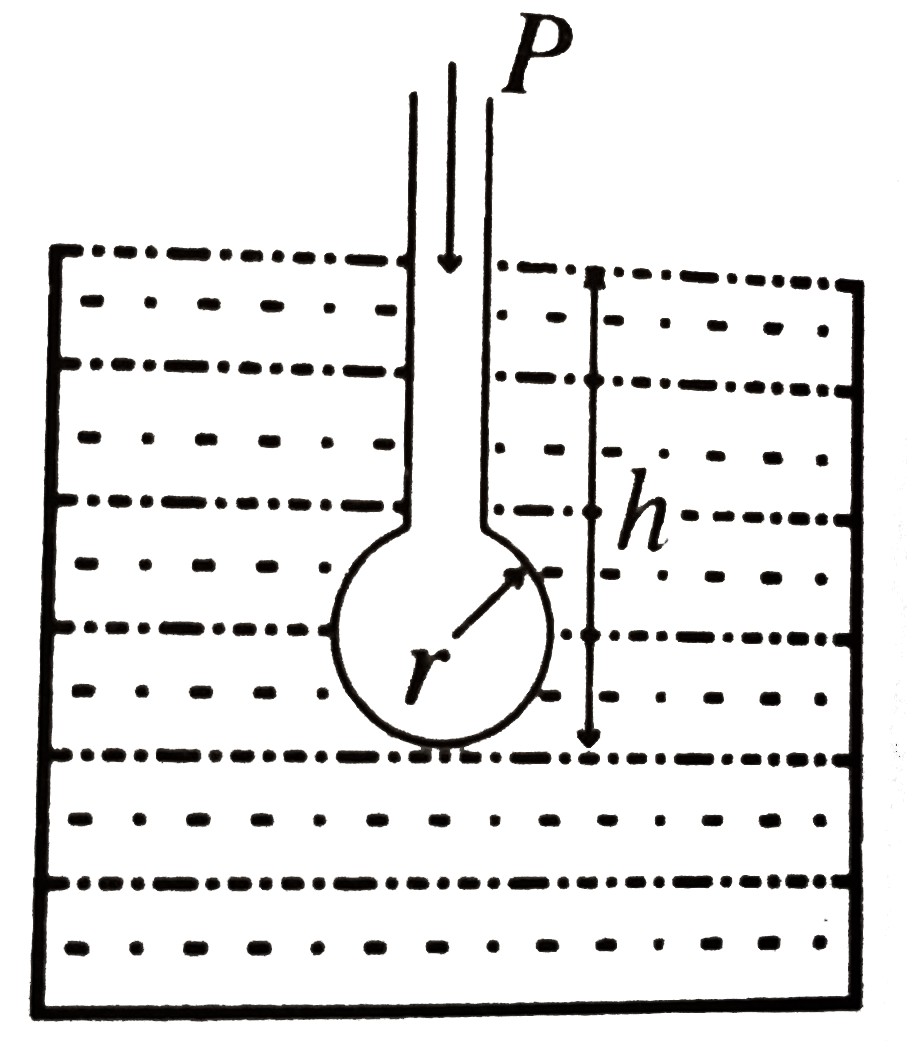
A narrow capillary tube is dipped $10 c m$ below water surface and a liquid bubble of radius $2 m m$ formed at the lower end by blowing air through the tube.
a. Calculate the excess pressure due to surface tension.
b. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water?
The surface tension of water at temperature of the experiment is $7.30 \times 10^{- 2} N / m$ . 1 atmospheric pressure $= 10^{5} P a$ , density of water $= 1000 k g / m^{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $1.01146 \times 10^{5}$

Updated on:21/07/2023

The surface tension for pure water in a capillary tube experiment is
A $\frac{ρ g}{2 h r}$
B $\frac{2}{h r ρ g}$
C $\frac{r ρ g}{2 h}$
D $\frac{h r ρ g}{2}$
A soap bubble of radius $10^{- 2}$ m is formed . The surface tension of the soap bubble is 0.04 N/m The excess of pressure inside the bubble is
A $160 N / m^{2}$
B $16 N / m^{2}$
C $1.6 N / m^{2}$
D $0.16 N / m^{2}$
At a depth of 5 m below the free surface of a liquid, an air bubble of radius 2 mm is formed. The pressure inside the bubble will be (The surface tension of water is $20 \times 10^{- 8} N/m.)$
A $2 \times 10^{5} N / m^{2}$
B $1.5 \times 10^{5} N / m^{2}$
C $3 \times 10^{5} N / m^{2}$
D $5 \times 10^{5} N / m^{2}$