An ideal fluid flows in the pipe as shown in the figure. The pressure in the fluid at the bottom P2 is the same as it is at the top P1. If the velocity of the top v1=2m/s. Then the ratio of areas A1.A2, is

2:1
4:1
8:1
4:3
The correct Answer is:B
Using equation of continuity we have v2=A1A2v1
From Bernoulli's theorem
p1+ρgh1+12ρh21
p2+ρgh2+12ρv22=g(h1−h2)=12(v22−v21)
⇒60=(A21A22−1)v21⇒A1A2=41
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
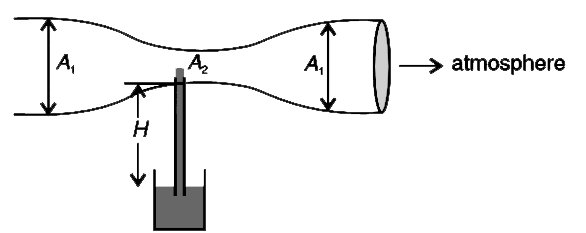
(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
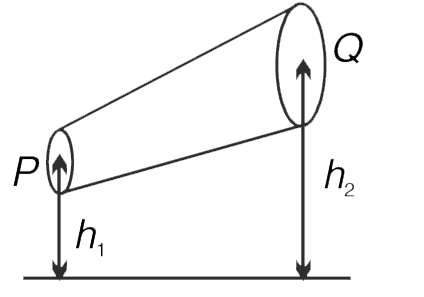
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View SolutionAn ideal fluid flows through a pipe of circular cross - section with diameters 5 cm and 10 cm as shown in the figure. The ratio of velocities of fluid at A and B is

View Solution
Knowledge Check
A liquid flows in a tube from left to right as shown in figure. A1 and A2 are the cross-section of the portions of the tube as shown. Then the ratio of speeds v1/v2 will be
 AA1/A2BA2/A1C√A2/√A1D√A1/√A2
AA1/A2BA2/A1C√A2/√A1D√A1/√A2A liquid flows in a tube from left to right as shown in figure. A1 and A2 are the cross-section of the portions of the tube as shown. Then the ratio of speeds v1/v2 will be
 AA1/A2BA2/A1C√A2/√A1D√A1/√A2
AA1/A2BA2/A1C√A2/√A1D√A1/√A2A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
A large tank of (height h1=4m ) water has a hose connected to it,as shown in figure.The tank is sealed at the top and has compressed air between the water surface and the top.When the water height h2 is 3m ,the gauge pressure of air P1=105Nm2 .Assume that the air above the water surface expands isothermally. The velocity of flow,out of the hose when h2 has decreased to 2m is √xg. Assume ideal fluid flow and Patm=105Nm2 .The value of x is (Neglect viscosity of liquid)
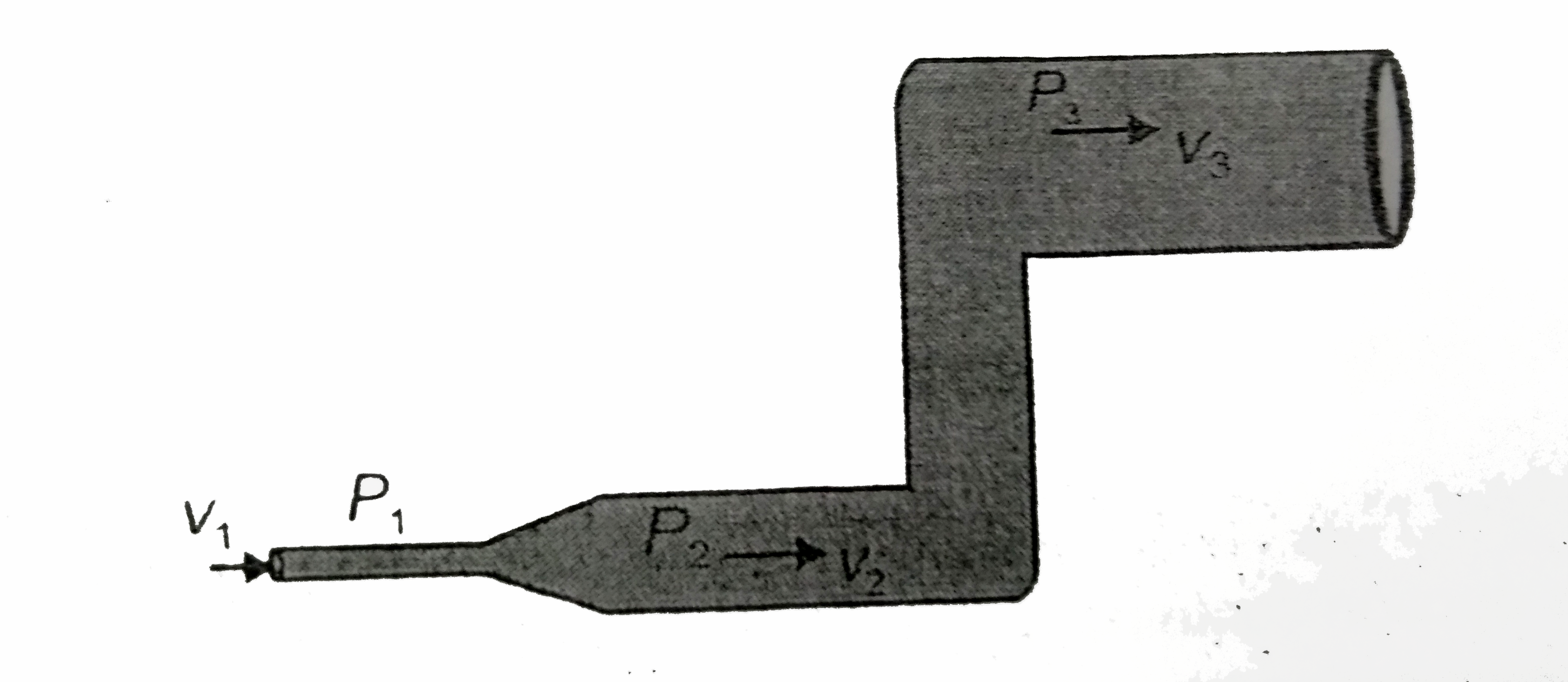
View SolutionWater is flowing through a pipe as shown in figure. If P1,P2andP3 are pressures and v1,v2andv3 are velocities of water at the different sections as shown in figure, then
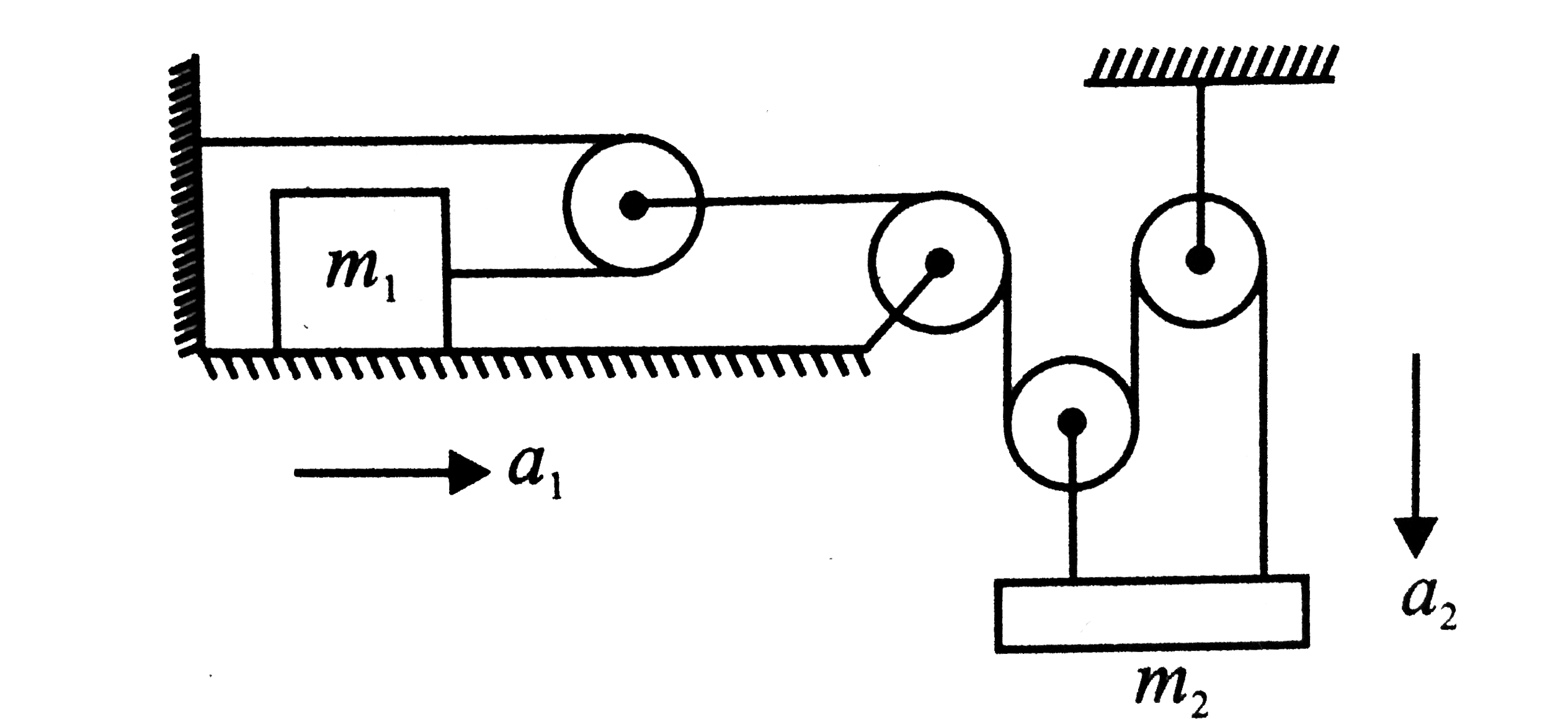
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionAn ideal fluid flows through a pipe of circular cross section with diameters 5 cm and 10 cm as shown. The ratio of velocities of fluid at A and B is

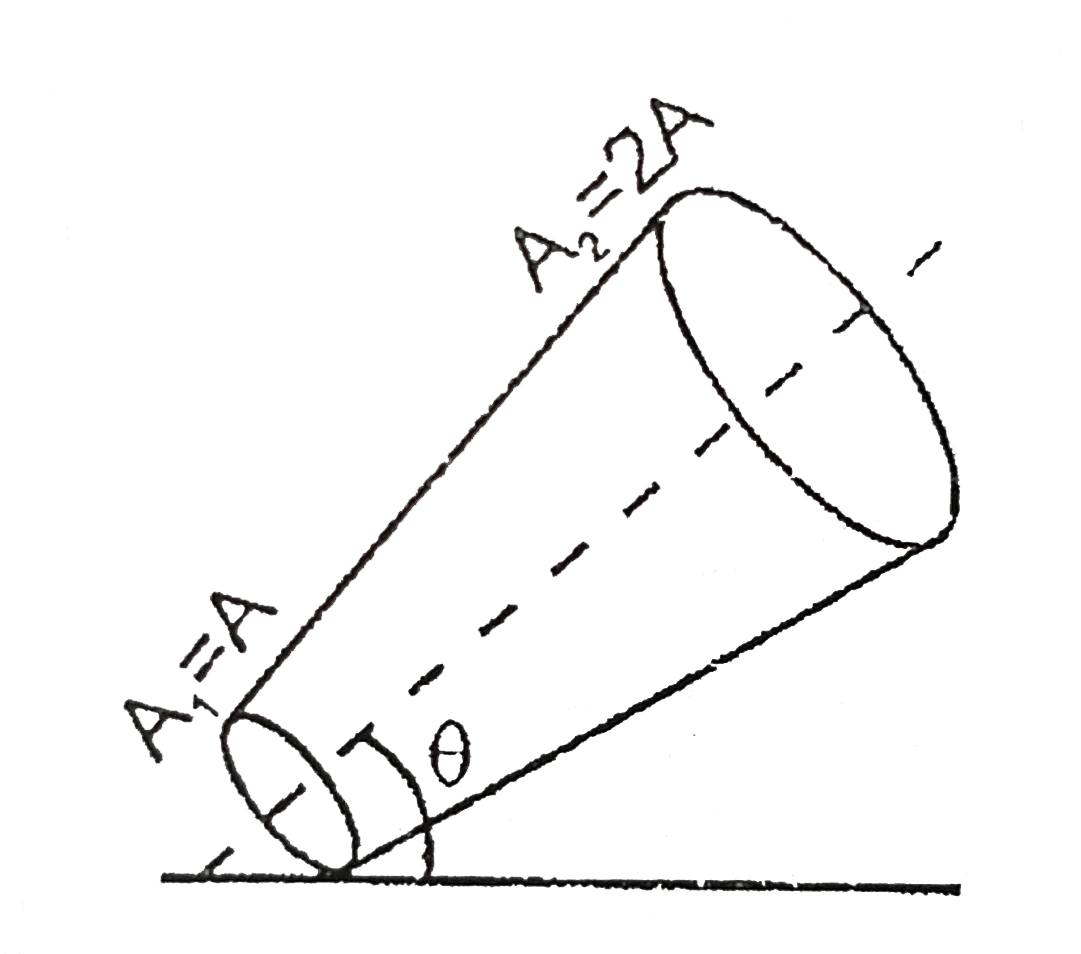
View SolutionA portion of a tube is shown in the figure. Fluid is flowing from cross-section area A1 to A2. The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A2 is √gl2. If the pressures at A1 & A2 are same, then the angle made by the tube with the horizontal will be:
View Solution

