Figure shows water filled in a symmetrical container. Four pistons of equal area A are used at the four openings to keep the water in equilibrium. Now an additional force F is applied at each piston. The increase in the pressure at the centre of the container due to this addition is

FA
2FA
4FA
0
The correct Answer is:A
The four pistons are initially in equilibrium. As additional force F is applied to each piston, the pressure in the fluid at each point must be increased by F.A so that each piston retains state of equilibrium. 
Thus the increment in the presure at each point is
△P=FA (by Pascal's law)
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
When a metallic sphere is released from the surface of water filled in a container of uniform area of cross section it is found to reach the bottom of the container in 2 s. If the density of the material of the sphere is 4.9gcm−3, calculate the pressure exerted by the liquid at the bottom of the container. Assume that only gravitational force and up-thrust act on the body.
View SolutionA gardener is watering plants at the rate 0.litre/sec using a pipe of cross-sectional area 1cm2 What additional force he has to exert if he desires to increase the rate of watering two times ? .
View Solution
Knowledge Check
As shown , a piston chamber pf cross section area A is filled with ideal gas. A sealed piston of mass m is right at the middle height of the cylinder at equilibrium. The friction force between the chamber wall and the piston can be ignored . The mass of the rest of the chamber is M.The atmosphere pressure is P0. Now slowly pull the piston upwards , find the maximum value of M such that the chamber can be lifted off the ground. The temperature remains unchanged.
_E01_049_Q01.png) AM=P0A−2mg2gBM=P0A−mg2gCM=P0A−mggDM=P0A2g
AM=P0A−2mg2gBM=P0A−mg2gCM=P0A−mggDM=P0A2gWhen pressure is applied through a piston at the top of a closed tube containing water, the pressure is transmitted to
AOnly the bottom of containerBAll directionsCOnly the side faces and the bottom of the containerDNone of theseFigure shows a long cylindrical container with ideal gas in two chambers. Lower chamber is filled with one mole of a mono atomic gas, while upper chamber has one mole of a diatomic gas. The gases initially are at temperature 300K, the container walls as well as pistons are conducting. Both the pistons are identical with mass 'M' and area 'A' such that MgA=P0 (atmosphere pressure).
Assuming the ideal gas constant to be R, answer the following questions:

The upper piston is pulled up slowly by 16cm and held there. the displacement of the lower piston till it reaches new equilibrium state is:A2cmB4cmC8cmD12cm
A gardener is watering plants at the rate 0.1 litre/sec using a pipe of cross - sectional area 1cm2. What additional force he has to exert if he desires to increase the rate of watering two times?
View SolutionA cylindrical container of height 3L and cross sectional area A is fitted with a smooth movable piston of negligible weight. It contains an ideal diatomic gas. Under normal atmospheric pressure P0 the piston stays in equilibrium at a height L above the base of the container. The gas chamber is provided with a heater and a copper coil through which a cold liquid can be circulated to extract heat from the gas. Volume occupied by the heater and the liquid coil is negligible. Following set of operations are performed to take the gas through a cyclic process.
(1) Heater is switched on. At the same time a tap above the cylinder is opened. Water fills slowly in the container above the piston and it is observed that the piston does not move. Water is allowed to fill the container so that the height of water column becomes L. Now the tap is closed.
(2) The heater is kept on and the piston slowly moves up. Heater is switched off at the time water is at brink of overflowing.
(3) Now the cold liquid is allowed to pass through the coil. The liquid extracts heat from the gas. Water is removed from the container so as to keep the position of piston fixed. Entire water is removed and the gas is brought back to atmospheric pressure.
(4) The circulation of cold liquid is continued and the piston slowly falls down to the original height L above the base of the container. Circulation of liquid is stopped. Assume that the container is made of adiabatic wall and density of water is ρ. Force on piston due to impact of falling water may be neglected.
(a) Draw the entire cycle on a P–V graph.
(b) Find the amount of heat supplied by the heater and the amount of heat extracted by the cold liquid from the gas during the complete cycle.
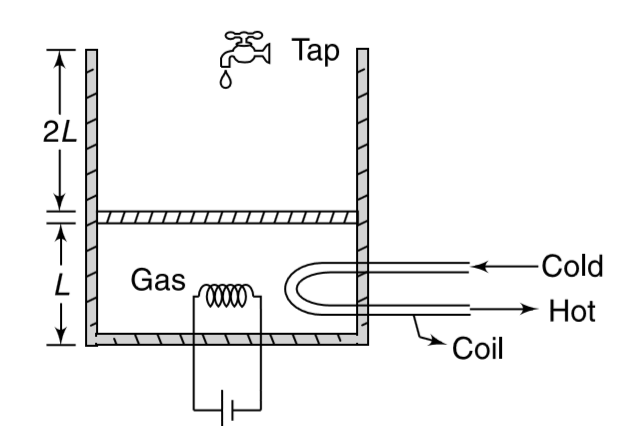
View SolutionInitial volume of H2 gas saturated with water vapour is confined under a piston in a container is 10 litres as shown in the given figure.

the container also contains some liquid water. The total pressure over liquid water is 80cm of Hg. If now the piston is removed such that volume of container is doubled, then final total pressure over liqid water in the container is P. The vapour pressure of water is 20cm of Hg and volume of liquid is negligible. Calculate P/10.........
View SolutionFigure shows a long cylindrical container with ideal gas in two chambers. Lower chamber is filled with one mole of a mono atomic gas, while upper chamber has one mole of a diatomic gas. The gases initially are at temperature 300K, the container walls as well as pistons are conducting. Both the pistons are identical with mass 'M' and area 'A' such that MgA=P0 (atmosphere pressure).
Assuming the ideal gas constant to be R, answer the following questions:

Total work done by the ideal gases in this process is
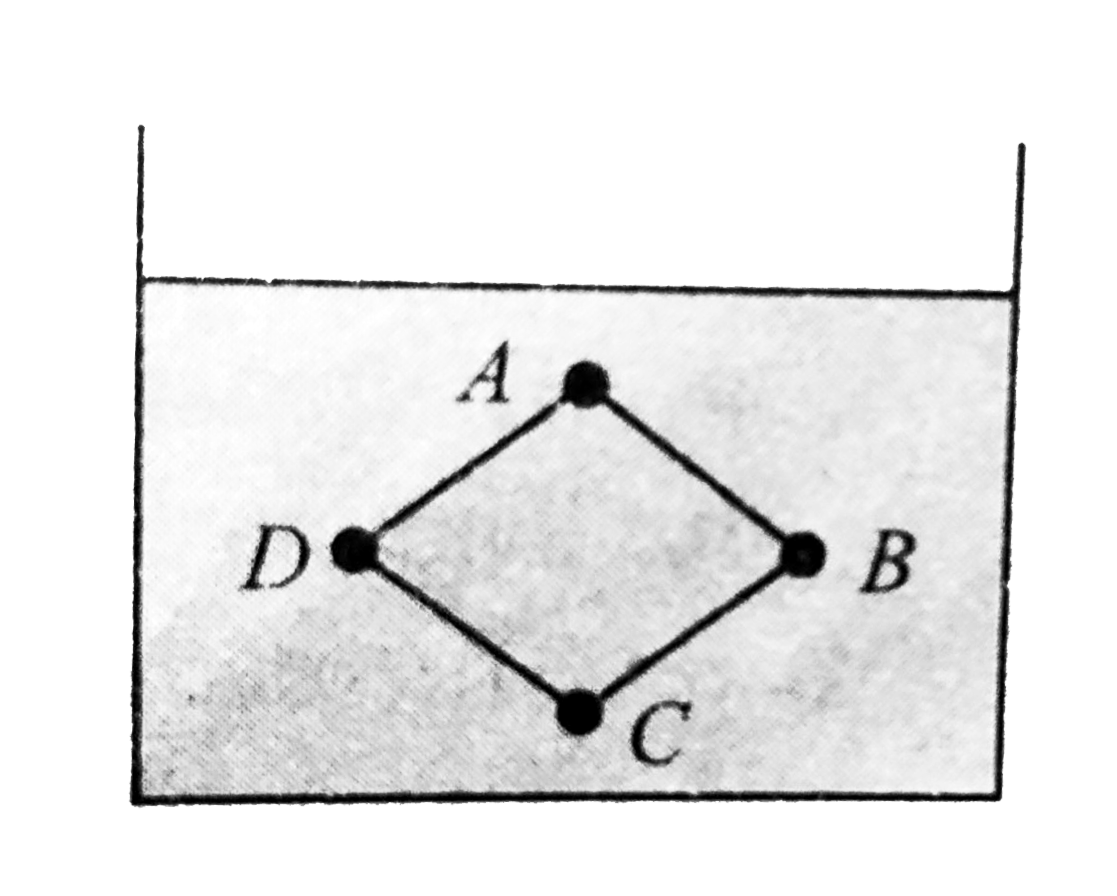
View SolutionFigure shows a container filled with a liquid of density ρ. Four points A,B,C and D lie on the vertices of a vertical square. Points A and C lie on a vertical line and points B and D lies on a horizontal line. Choose the correct statement(s) about the pressure at the four points.
View Solution

