A non-uniform cylinder of mass m, length l and radius r is having its centre of mass at a distance l.4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is l. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

πρgl2r2I
πρgl2r24I
πρgl2r22I
3πρgl2r24I
The correct Answer is:B
Torque about CM 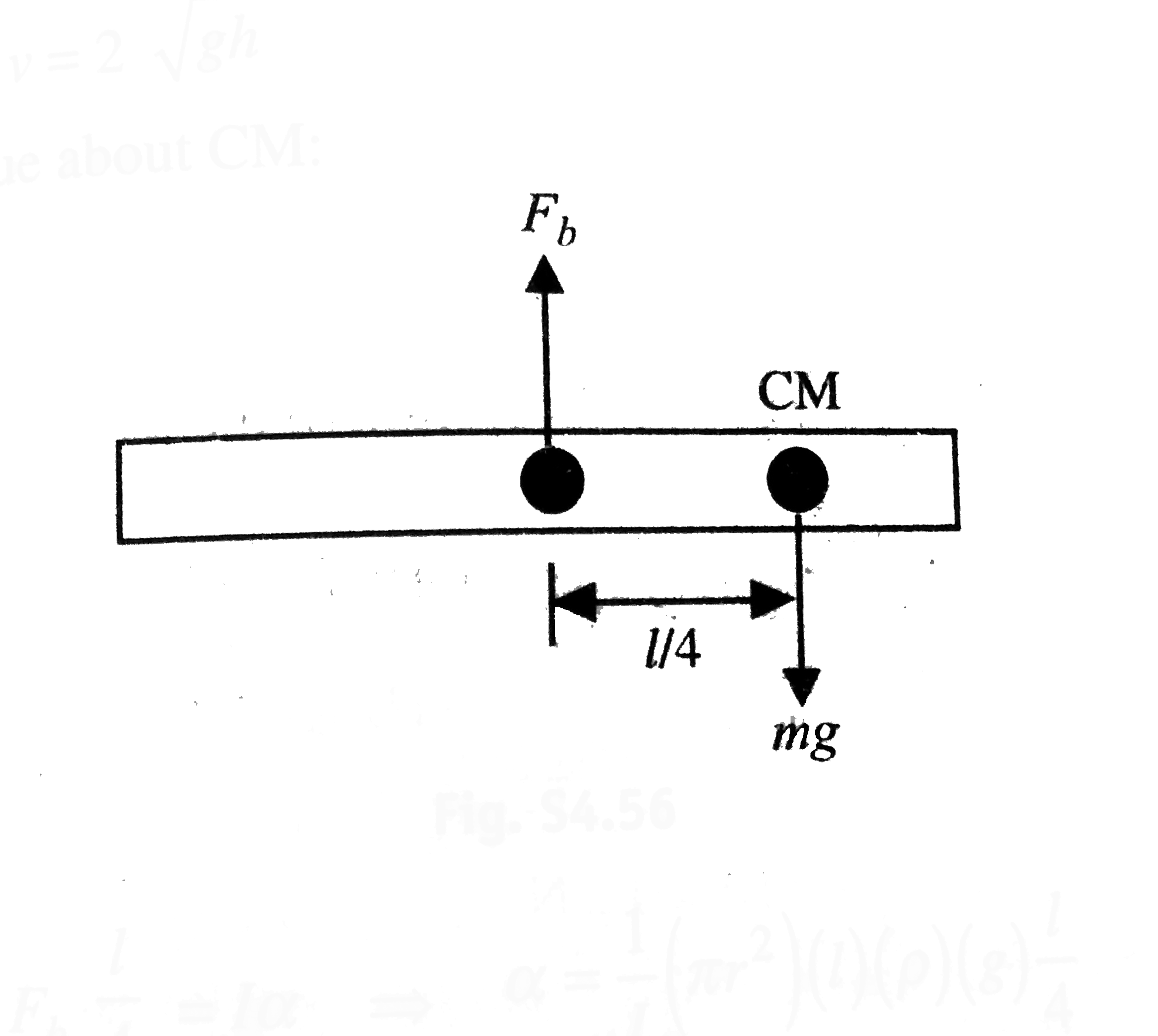
Fbl4=Iα⇒α=1I(πr2)(l)(ρ)(g)l4
⇒α=πr2l2gρ4I
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
What is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
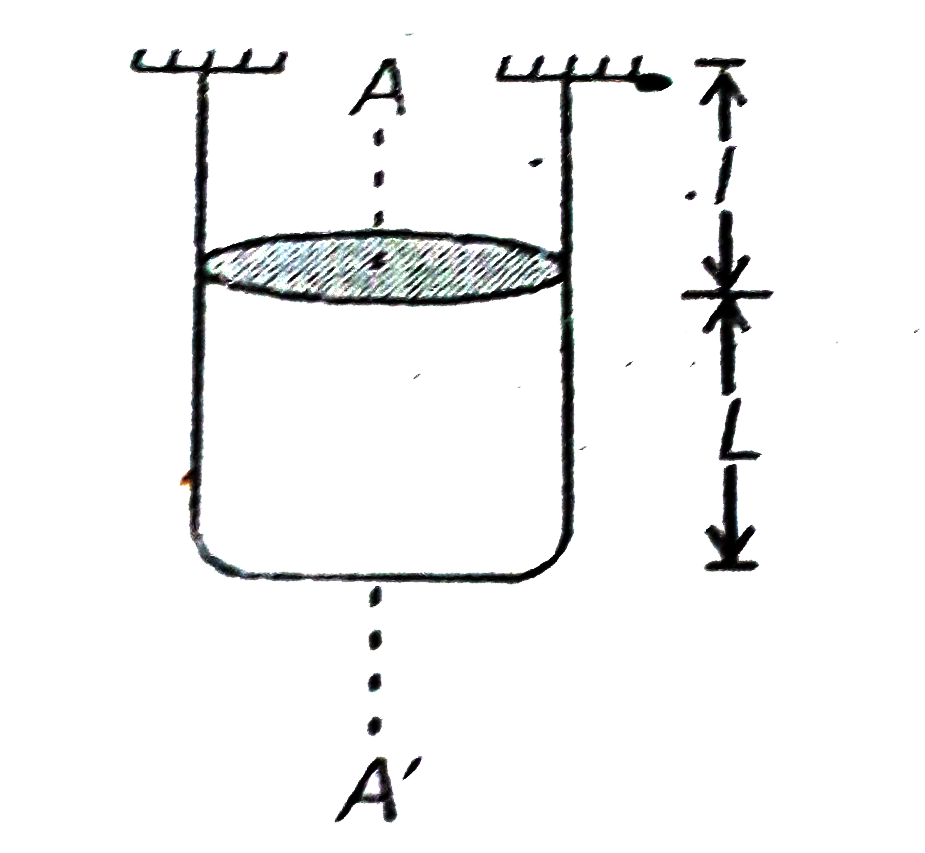
View Solution
Knowledge Check
A non uniform cylinder of mass m, length l and radius r having its C.O.M at a distance l4 from centre and lying on axis of cylinder . The cylinder is kept in a liquid of unifrom density ρ. The moment of inertia of the rod about C.O.M is I. The angular acceleration of point A relative to point B just after the rod is released from position shown in figure is .
 Aπρgl2r22IB3πρgl2r24ICπρgl2r2IDπρgl2r24I
Aπρgl2r22IB3πρgl2r24ICπρgl2r2IDπρgl2r24IA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is :
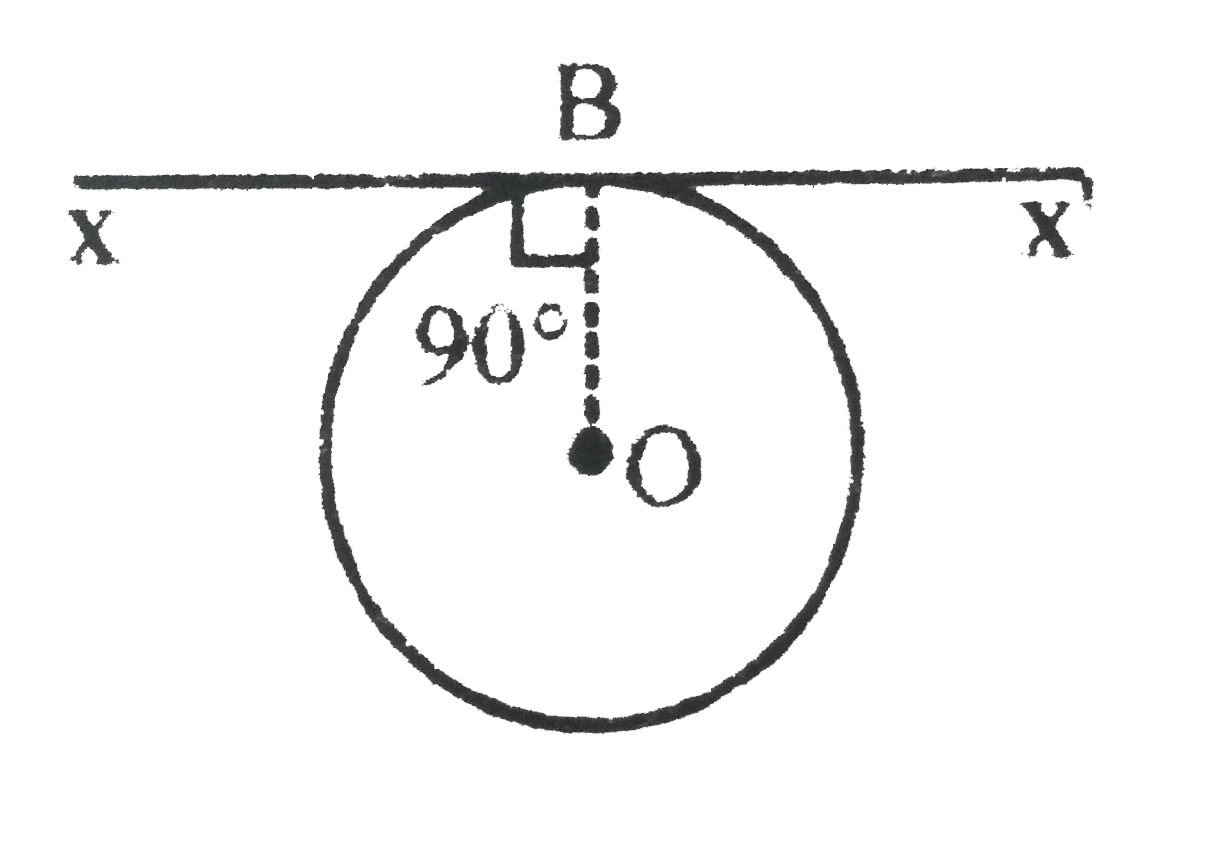 .AρL38π2BρL316π2C5ρL316π2D3ρL38π2
.AρL38π2BρL316π2C5ρL316π2D3ρL38π2A thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is :
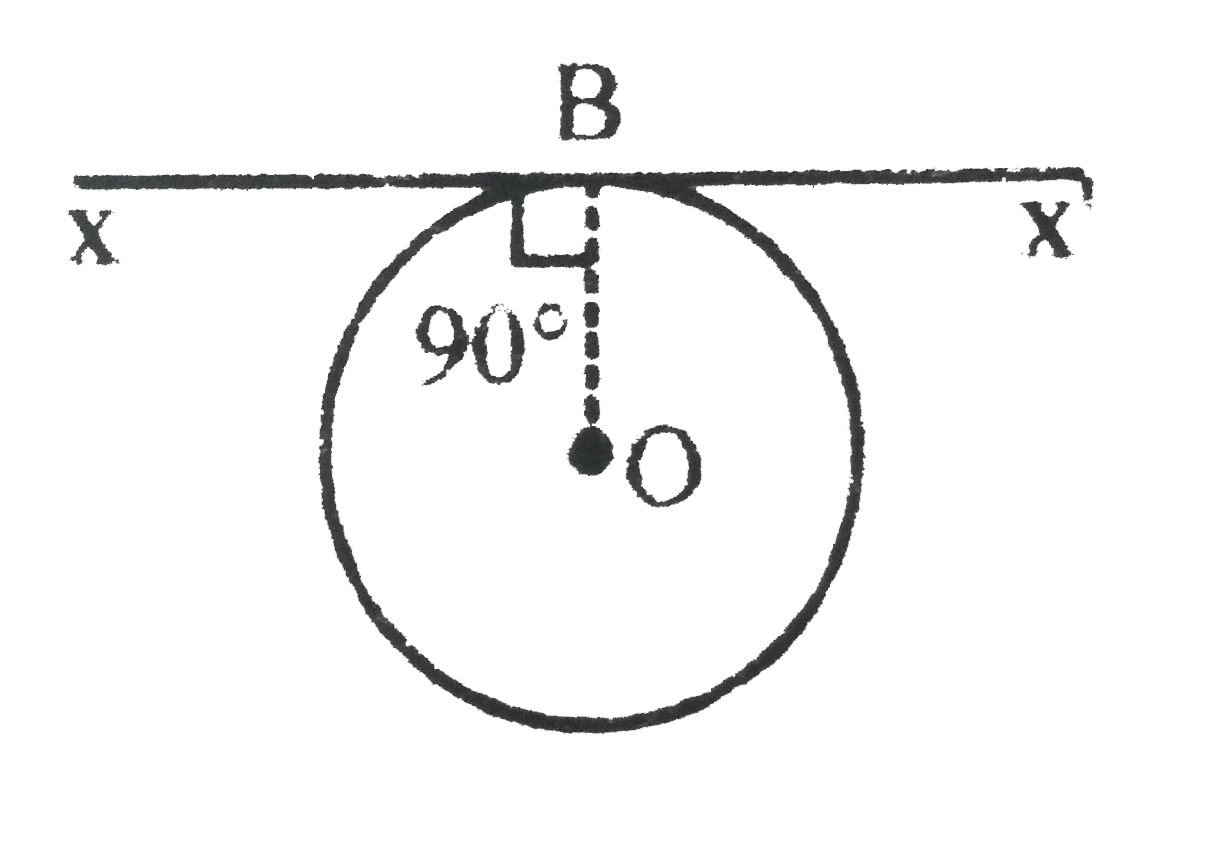 .AρL3/8π2BρL3/16π2C5ρL3/16π2D3ρL3/8π2.
.AρL3/8π2BρL3/16π2C5ρL3/16π2D3ρL3/8π2.
A square sheet of edge length L and uniform mass per unit area (σ) is used to form a hollow cylinder.The moment of inertia of this cylinder about the central axis is
View SolutionMoment of inertia of a hollow cylinder of mass M and radius R, about the axis of cylinder is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View Solution

