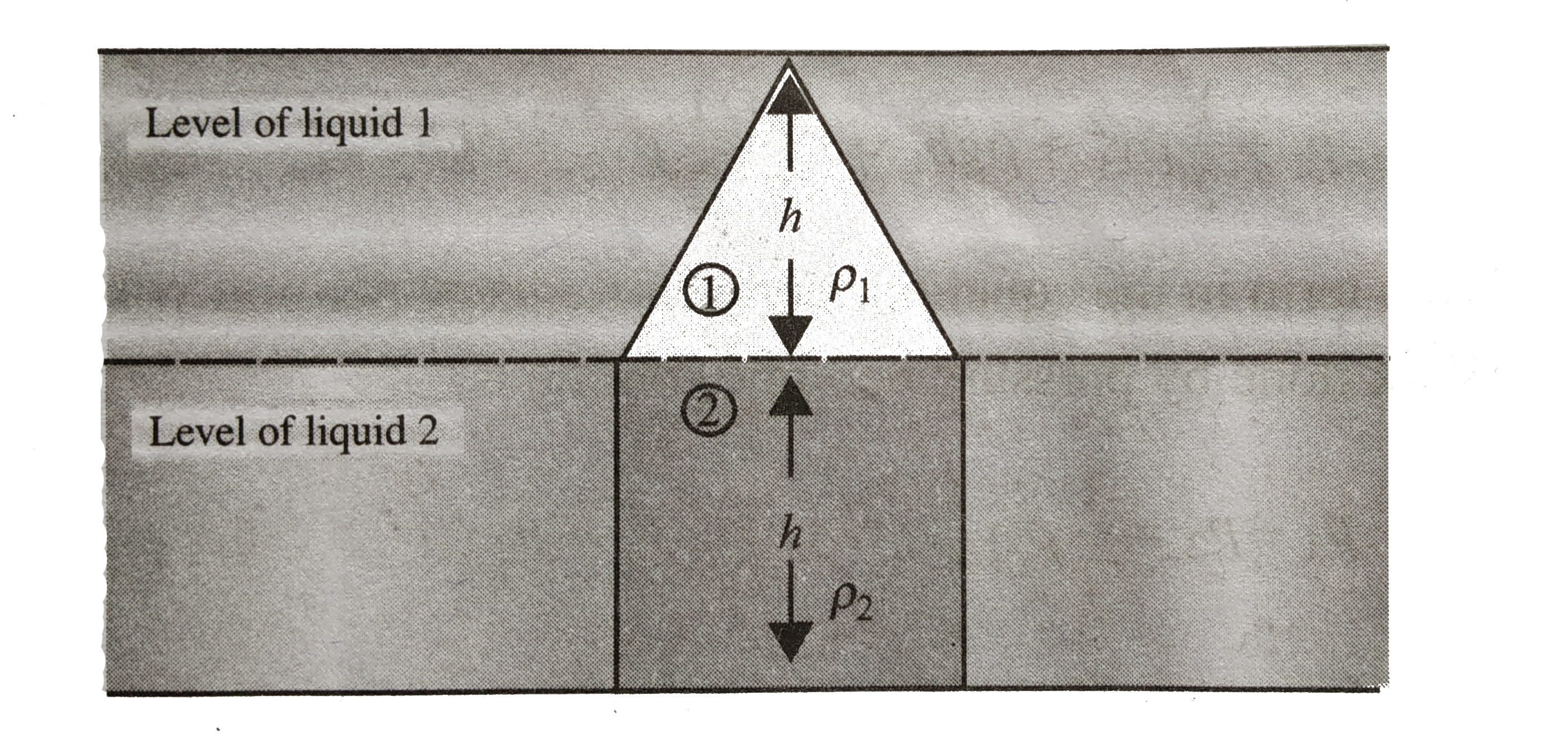
A composite plate comprises a triangular area (1) and rectangular area (2) as shown in the figure. The triangular plate experiences forces due to the liquids of densities ρ1 and the rectangular plate experiences the force due to liquid of density ρ2. Find the hydrostatic forces on (a) area 1, (b) area 2, (c) total composite area of the plate. Assume ρ1=ρ and ρ2=2ρ.
The correct Answer is:73ρgh2b
The hydrostatic force on the triangular area is
F1=ρ1ghC1A1
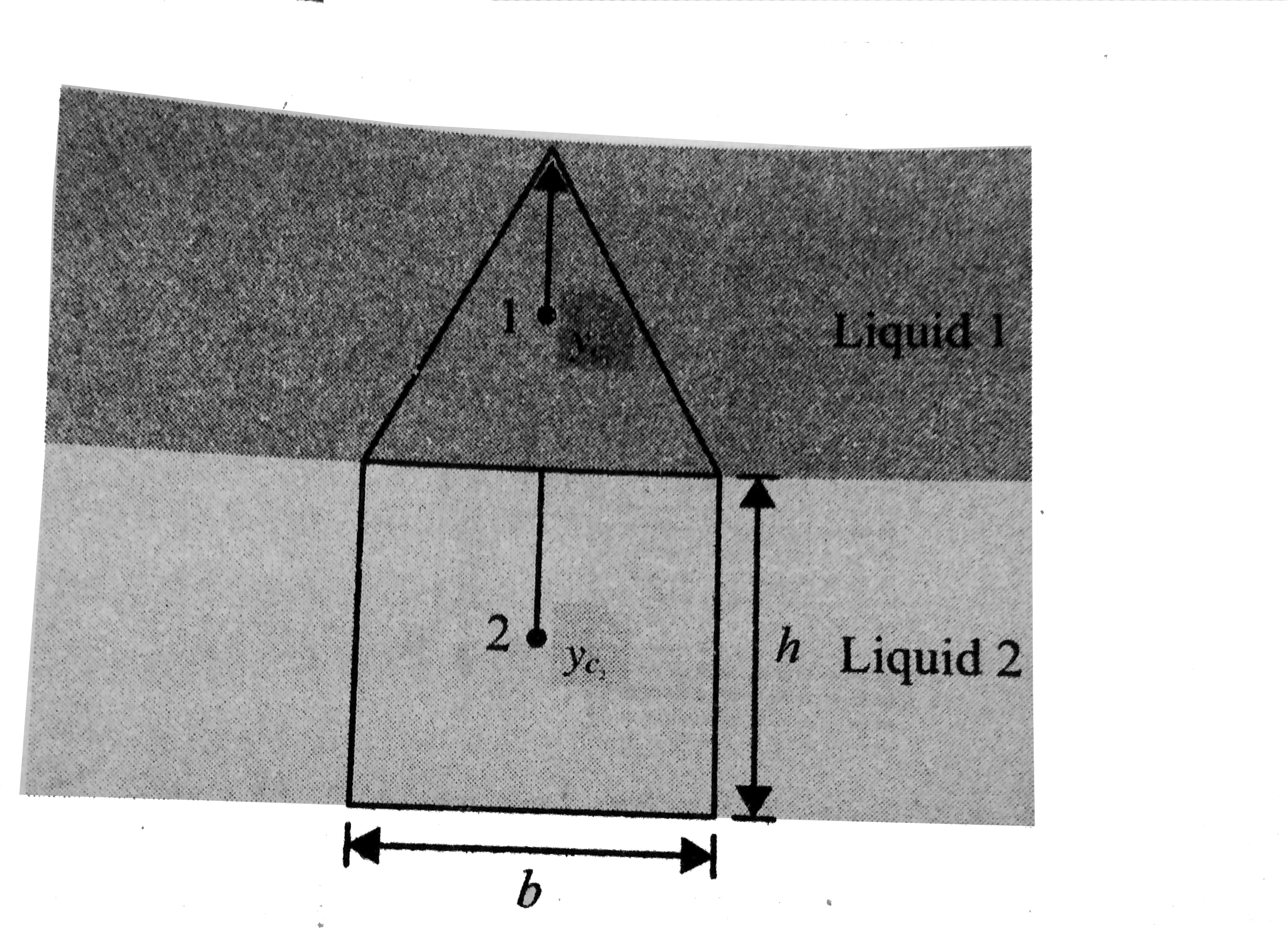
where ρ1=ρ,yC1=2h3 and A1=bh2. This gives
F1=ρgh2b3
b. The hydrostatic force on the rectangular area is
F2=(ρ1gh1+ρ2ghyC2)A2
Substituting ρ1=ρ,h1=h,ρ2=2ρ,yC2=h/2 and A2=bh we have F2=ρgh2b.
c. The total hydrostatic force on the composite patch is
F=F1+F2=ρ3gh2b+2ρgh2b=73ρgh2b
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionHalf of the recrtangular plate shown in figure is made of a material of density ρ1 and the other half of density ρ2. The length of the plate is L. Locate the centre of mass of the plate.

View Solution
Knowledge Check
If two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2If two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2If two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2roh1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2
A ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionA triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
View SolutionA composite rod made up of two conductors of resistivity ρ1 and ρ2 is shown in the figure. If face A and B are connected to a battery, find the resistance of the rod.
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View Solution
