The steel balls $A$ and $B$ have a mass of $500 g$ each and al rotating about the vertical axis with an angular velocity of $4 r a d / s$ at a distance of $15 C M$ from the axis. Collar $C$ is now forced down until the balls are at a distance $5 C M$ from the axis. How Much work must be done move the collar down?

Video Solution

Text Solution

Verified by Experts

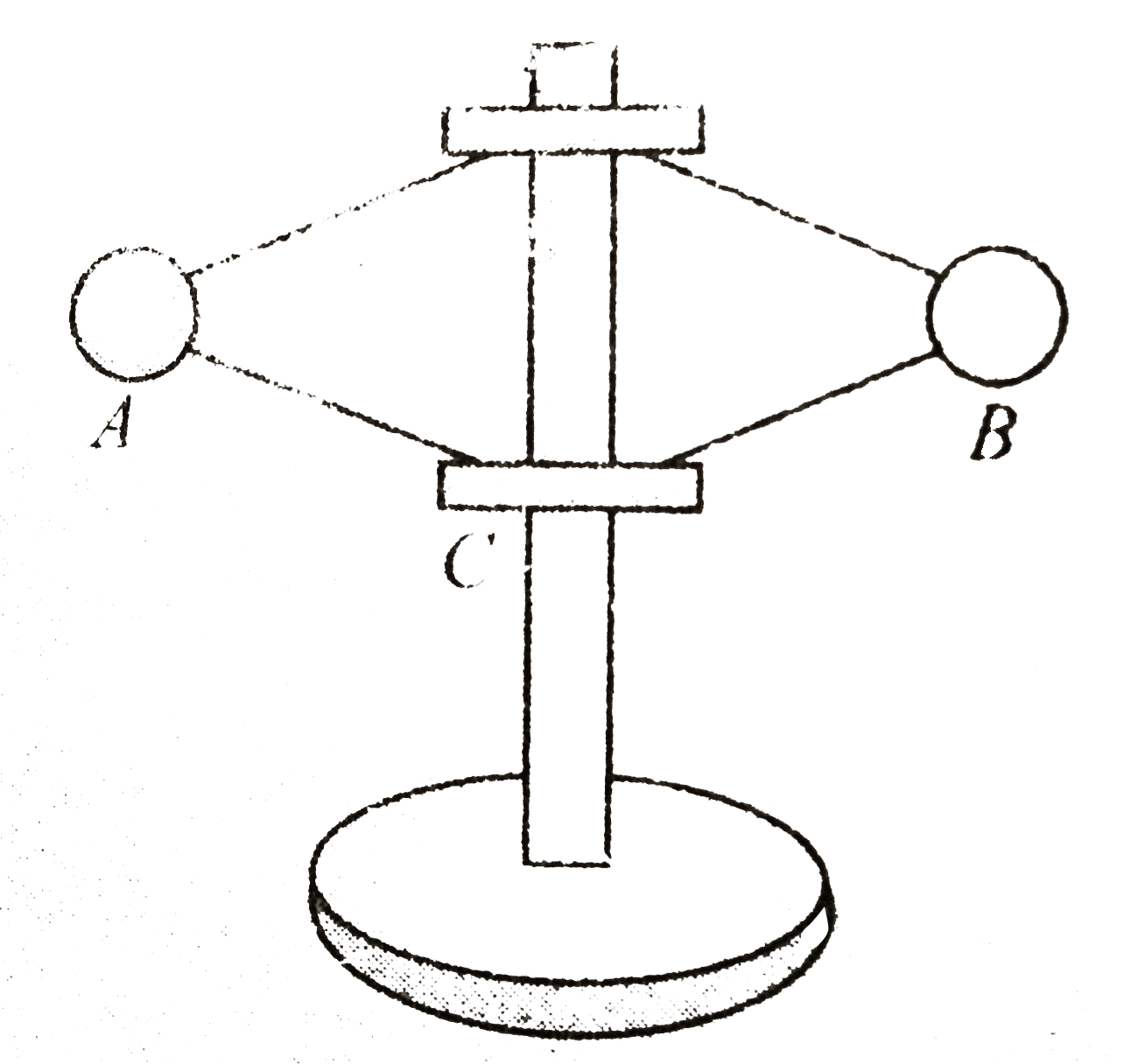
In process angular momentum remains constant
$I_{1} ω_{1} = I_{2} ω_{2}$
Where $I_{1} = 2 m {(0.15)}^{2}, ω_{1} = 4 r a d / s$
$I_{2} = 2 m {(0.05)}^{2}$
Substituting these values in above equation, we get
$ω_{2} = \frac{I_{1} ω_{1}}{I_{2}} = 36 r a d / s$
Work done on the collar
$W = \frac{1}{2} I_{2} ω_{2}^{2} - \frac{1}{2} I_{1} ω_{1}^{2}$
or $W = \frac{1}{2} {(0.05)}^{2} \times 36^{2} - \frac{1}{2} 2 m {(0.015)}^{2} \times 4^{2}$
where $m = \frac{500}{1000} = 0.05 k g = 1.44 J$

Updated on:21/07/2023

A homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis with an angular velocity of 4 rad/s. the linear momentum of the disc is
A1.2 kg m/s
B1.0 kg m/s
C0.6 kg m/s
Dzero
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A circular of radius 20 cm is rotating about its own axis at an angular velocity $ω$ . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
A $2 ω$
B $ω / 2$
C $ω$
D $ω / 4$