A rod of mass m spins with an angular speed ω=√gl, Find its a. kinetic energy of rotation. b. kinetic energy of translation c. total kinetic energy.

Video Solution
Text Solution
Kinetic enegy of rotation Krotational=12ICω2
=12(ml212)(√gl)2=124mlgl
b Kinetic energy of translation, Krotational=12mv2C
=12m[(ωl2)2]=12m[√gl×l2]2=13mgl
c. total kinetic energy
Ktotal=Ktranslational+Krotational
=16mgl=12IPω2=12[ml22][√gl]2=16mgl
|
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.3
Explore 21 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
Knowledge Check
The rotational kinetic energy is -
Amω2B12Iα2C12Iω2D12mv2Rotational kinetic energy is equal to
A1w2BI2w2C32Iw2D12Iw2What fraction of translational kinetic energy of rolling circular disc to total kinetic energy ?
A1/3B1C2/3D1/2
Rotational Kinetic Energy || Examples
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
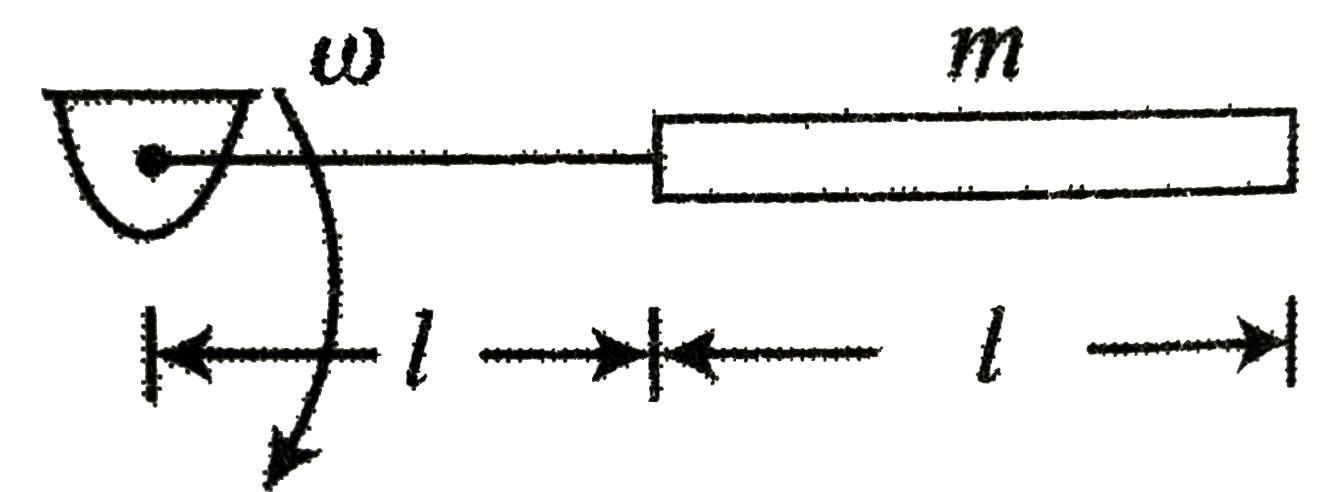
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionWhen a sphere rolls without slipping the ratio of its kinetic energy of translation to its total kinetic energy is.
View SolutionA ring is rolling without slipping. Its energy of translation is E. Its total kinetic energy will be :-
View SolutionIf rotational kinetic energy is 50% of total kinetic energy then the body will be
View Solution

