A uniform disc of mass m is fitted (pivoted smoothly) with a rod of mass m/2. If the bottom of the rod os pulled with a velocity v, it moves without changing its orientation and the disc rolls without sliding. The kinetic energy of the system (rod + disc) is.
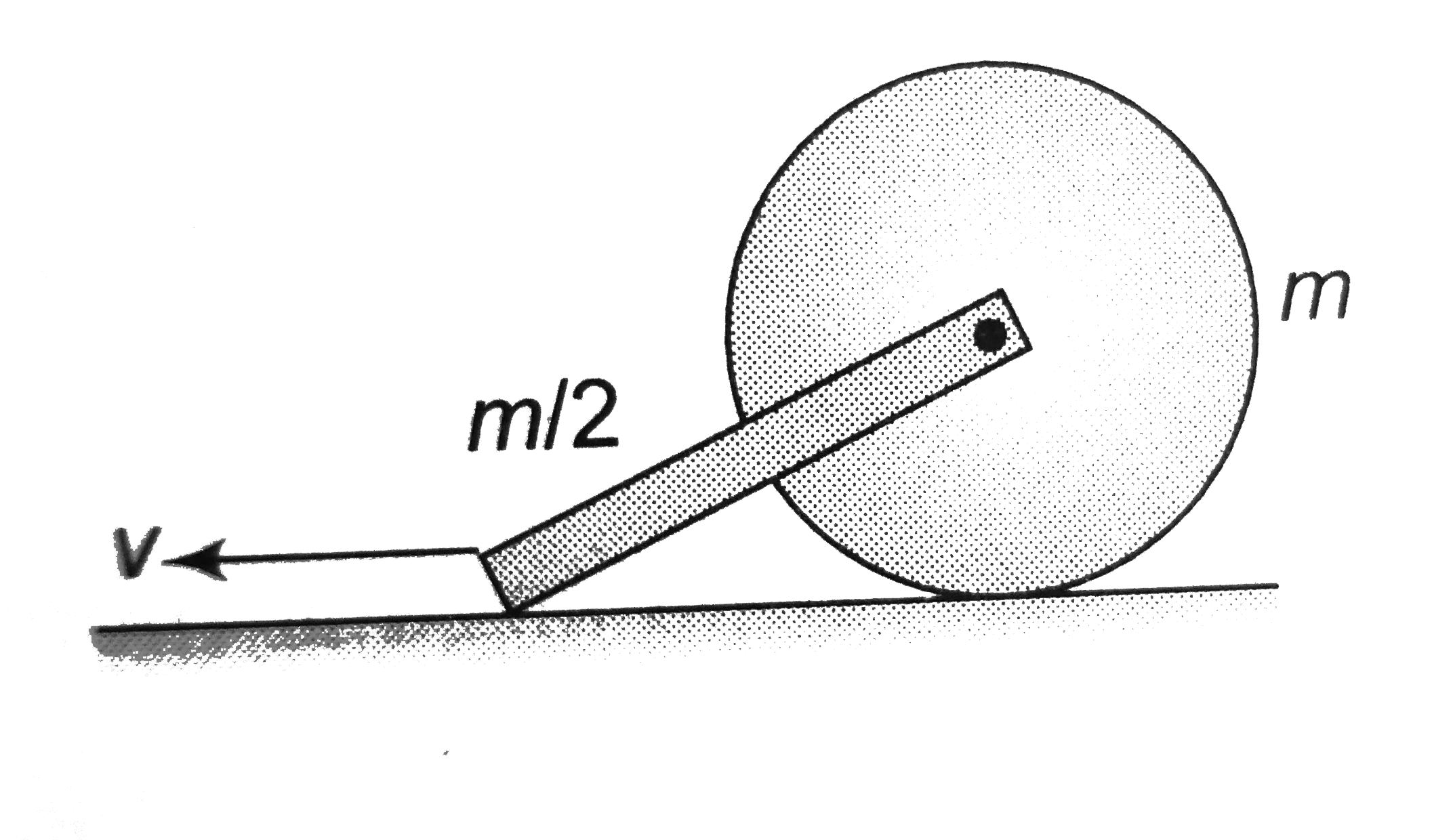 .
.
Rolling can be considered as pure rotation about point of contact
Krolling=12IPIω2
=12(mR22+mR2)ω2=34mR2ω2……..i
The rod translates with the velocity v hence velocity of centre of disc will also be v
V=ωR ............ii
Form i and ii Krolling=34mv2
Kinetic energy of the rod Krod=12(m2)v2=mv24.........iii
Ktotal=krolling+krod=mv2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.3
Explore 21 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
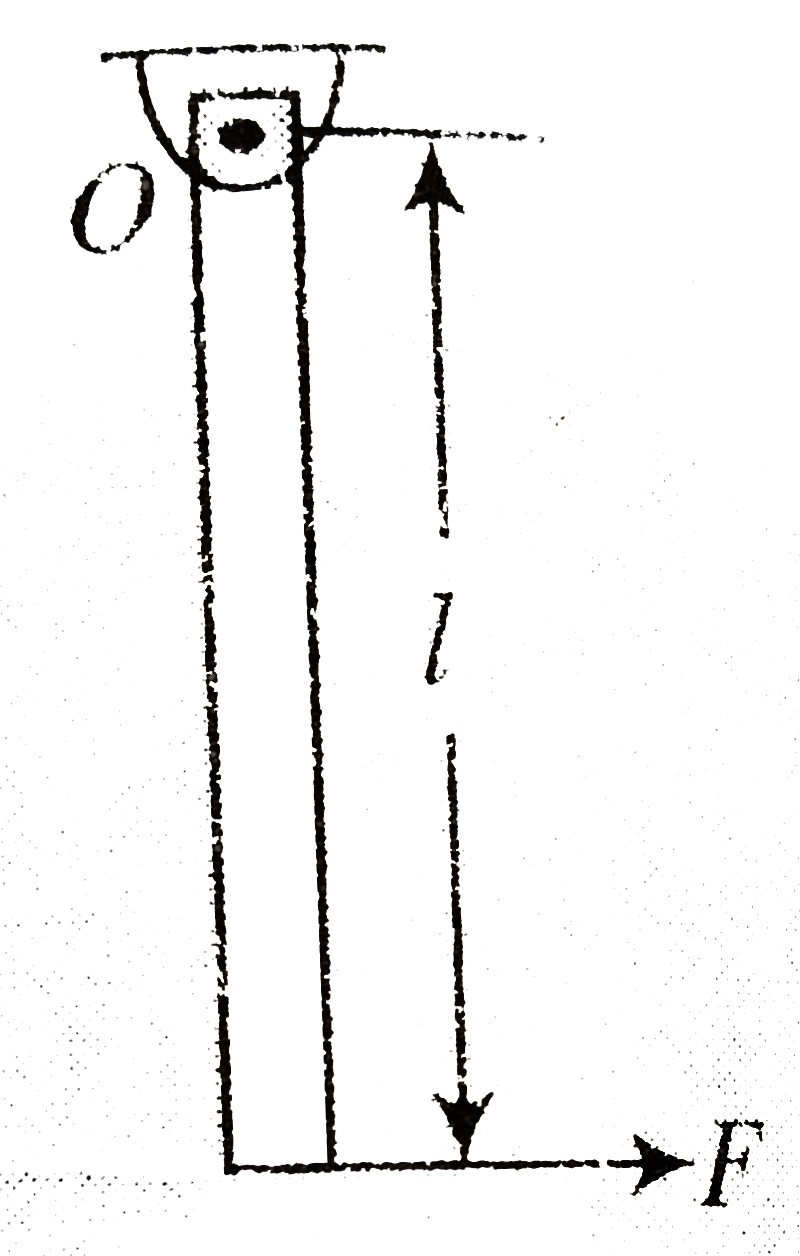
View SolutionA rod touches a disc kept on a smooth horizontal plane. If the rod moves with an acceleration a, the disc rolls on the rod without acceleration a, the disc rools on therod without slidding. Then , the acceleration of the disc w.r.t the rod is

View Solution
Knowledge Check
A uniform disc of mass m is fitted (pivoted smoothly) with a rod of mass m/2. If the bottom of the rod os pulled with a velocity v, it moves without changing its and of orientation and the disc rolls without sliding. Take kinetic energy of the system (rod + disc) is.
 .Amv24Bmv22C5mv216Dmv2
.Amv24Bmv22C5mv216Dmv2A circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
A10 JB6 JC2 JD4 JFour beads each of mass m are glued at the top, bottom and the ends of the horizontal diameter of a ring of massm. If the ring rolls without sliding with the velocity v of its, the kinetic energy of the system (beads+ring) is
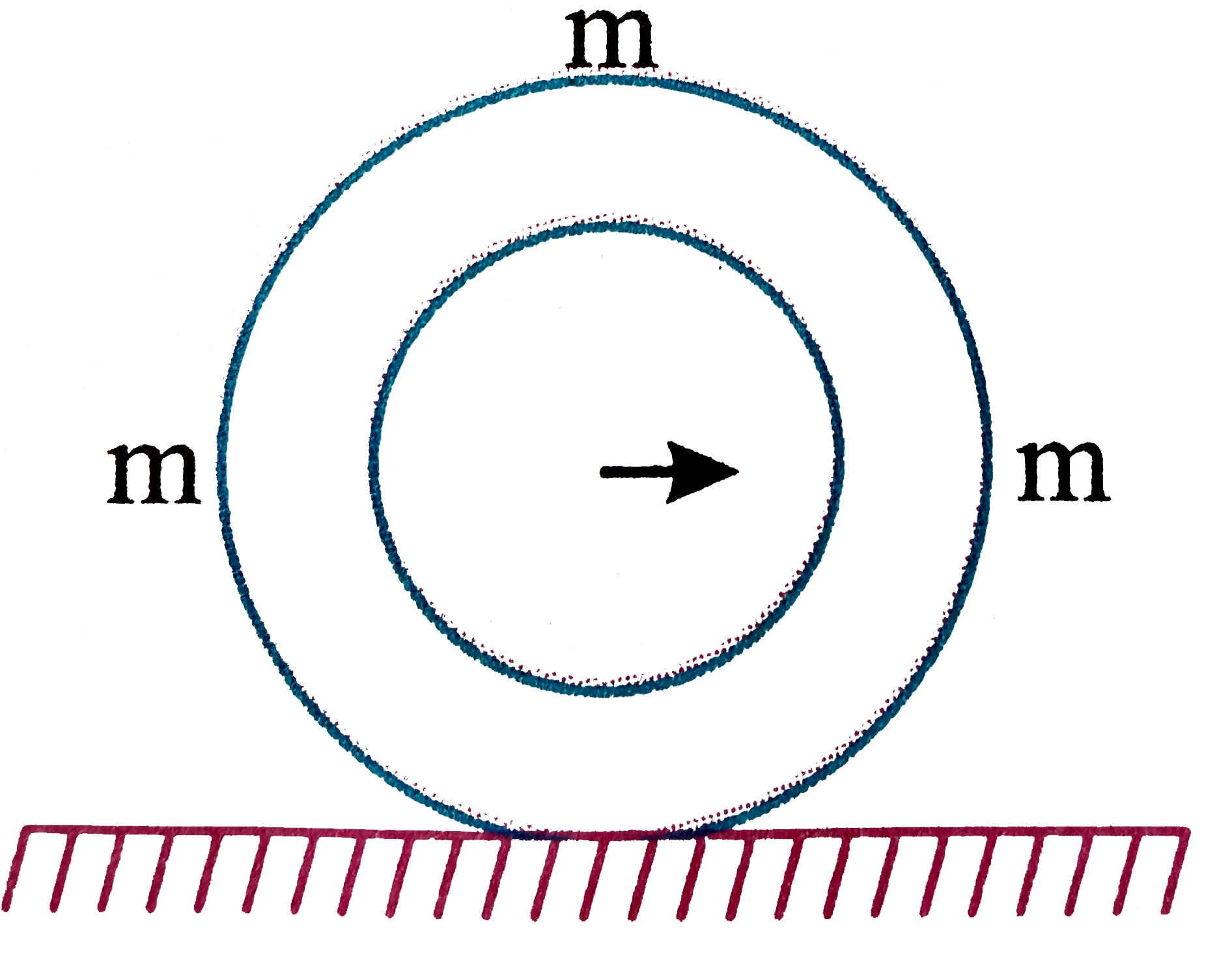 A5mv2B4mv2C2mv2Dmv2
A5mv2B4mv2C2mv2Dmv2
A ring of mass m is rolling without slipping with linear velocity v as shown is figure. A rod of identical mass is fixed alone one of its diameter. The total kinetic energy of the system is
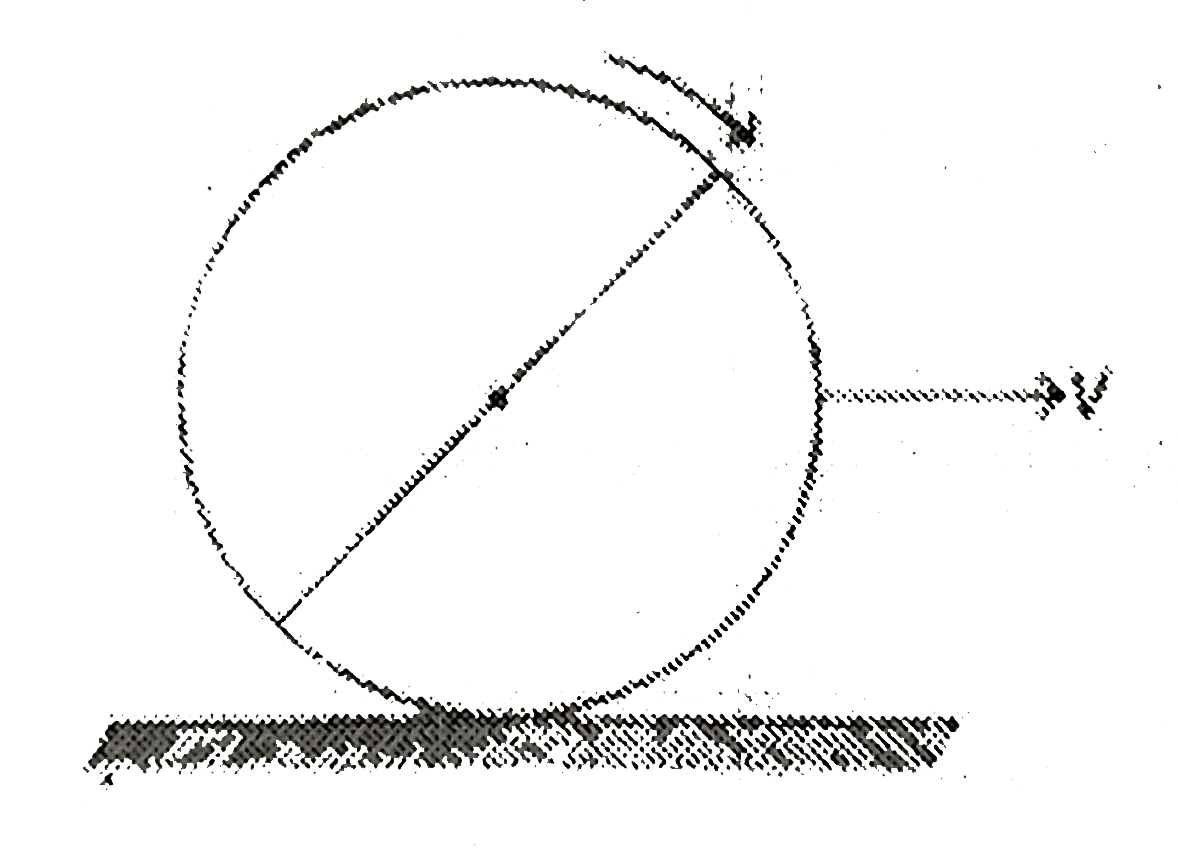
View SolutionA circular disc of mass 0.41 kg and radius 10 m rolls without slipping with a velocity of 2 m/s. The total kinetic energy of disc is
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

View Solution

