Four identical rods are joined end to end to form a square. The mass of each rod is . The moment of inertia of the square about the median line is
none of these
The correct Answer is:D
To find the moment of inertia of a square formed by four identical rods about the median line, we can follow these steps:
1. Identify the Configuration:
- We have a square formed by four identical rods, each of mass M and length L.
2. Determine the Axis of Rotation:
- The median line in this case is the line that bisects the square horizontally (or vertically). This line runs through the center of the square and is perpendicular to the length of the rods.
3. Calculate the Moment of Inertia for Each Rod:
- For the two horizontal rods (let's call them Rod 1 and Rod 2), the moment of inertia about the median line can be calculated using the formula for a rod about an axis through its center:
I=112ML2
- Since there are two horizontal rods, the total moment of inertia for these rods is:
Ihorizontal=2×112ML2=16ML2
4. Calculate the Moment of Inertia for the Vertical Rods:
- For the two vertical rods (Rod 3 and Rod 4), we need to use the parallel axis theorem because their axis of rotation is not through their center. The distance from the median line to the center of each vertical rod is L2.
- The moment of inertia for each vertical rod about its own center is:
Icenter=112ML2
- Using the parallel axis theorem:
Ivertical=Icenter+Md2
where d=L2:
Ivertical=112ML2+M(L2)2=112ML2+ML24=112ML2+312ML2=412ML2=13ML2
- Since there are two vertical rods, the total moment of inertia for these rods is:
Ivertical=2×13ML2=23ML2
5. Combine the Moments of Inertia:
- The total moment of inertia of the square about the median line is the sum of the moments of inertia of all four rods:
Itotal=Ihorizontal+Ivertical=16ML2+23ML2
- To combine these, convert 23 to sixths:
23=46
- Thus,
Itotal=16ML2+46ML2=56ML2
Final Result:
The moment of inertia of the square about the median line is:
I=56ML2
- We have a square formed by four identical rods, each of mass M and length L.
- The median line in this case is the line that bisects the square horizontally (or vertically). This line runs through the center of the square and is perpendicular to the length of the rods.
- For the two horizontal rods (let's call them Rod 1 and Rod 2), the moment of inertia about the median line can be calculated using the formula for a rod about an axis through its center:
I=112ML2
- Since there are two horizontal rods, the total moment of inertia for these rods is:
Ihorizontal=2×112ML2=16ML2
- For the two vertical rods (Rod 3 and Rod 4), we need to use the parallel axis theorem because their axis of rotation is not through their center. The distance from the median line to the center of each vertical rod is L2.
- The moment of inertia for each vertical rod about its own center is:
Icenter=112ML2
- Using the parallel axis theorem:
Ivertical=Icenter+Md2
where d=L2:
Ivertical=112ML2+M(L2)2=112ML2+ML24=112ML2+312ML2=412ML2=13ML2
- Since there are two vertical rods, the total moment of inertia for these rods is:
Ivertical=2×13ML2=23ML2
- The total moment of inertia of the square about the median line is the sum of the moments of inertia of all four rods:
Itotal=Ihorizontal+Ivertical=16ML2+23ML2
- To combine these, convert 23 to sixths:
23=46
- Thus,
Itotal=16ML2+46ML2=56ML2
The moment of inertia of the square about the median line is:
I=56ML2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Multiple Correct
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Subjective
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
AB and CD are two identical rods each of length l and mass m joined to form a cross. The moment of inertia of these two rods about a bisector (xy) of the angle between the rods is:

View SolutionFour thin metal rods, each of mass M and length L, are welded to form a square ABCD as shown in figure. The moment of inertia of composite structure about a line which bisects rods AB and CD is
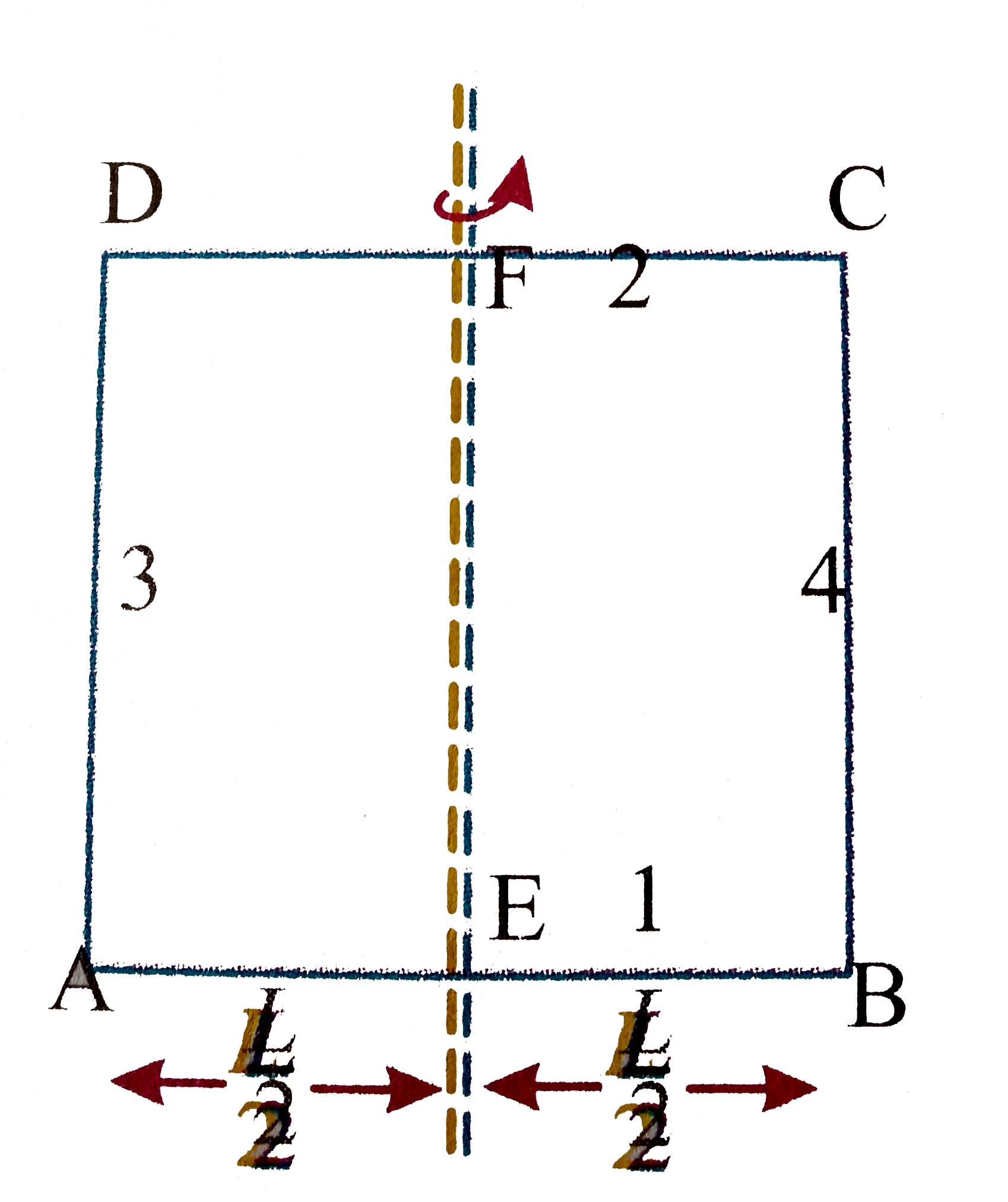
View Solution
Knowledge Check
Two identical rods are joined to form an 'X'. The smaller angle between the rods is θ. The moment of inertia of the system about an axis passing through point of intersection of the rods and perpendicular to their plane is proportional to:
AθBsin2θCcos2θDindependent of θTwo identical iniform rods are joined to from a symmetrical 'X'. The smaller angle between the rods is θ. The moment of inertia of the system about an axis passing through point of intersection of the rods and perpendcular to their plane is proportional to :
Asin2θBθCcos2θDindependent of θFour thin uniform rods each of length L and mass m are joined to form a square . The moment of inertia of square about an axis along its one diagonal is
AmL26B23mL2C3mL24D4mL23
Four identical rods of same material are joined end to end to form a square. If the temperature difference between the ends of a diagonal is 100∘C, then the temperature difference between the ends of other diagonal will be
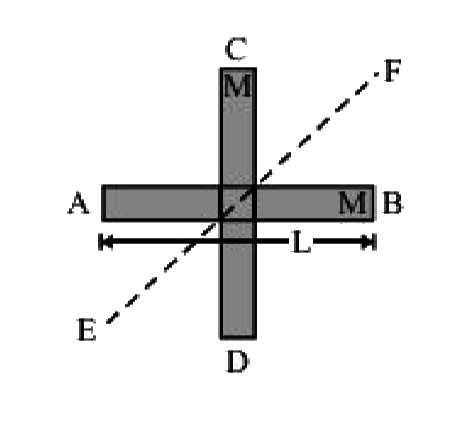
View SolutionTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
View SolutionFour identical thin rods each of mass M and length l3, form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is---
View SolutionFour identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionThree thin rods, each of length 2 m and mass 3 kg are placed along x, y and z axes, such that one end of each rod is at the origin. The moment of inertia of this system about the x axis is
View Solution
