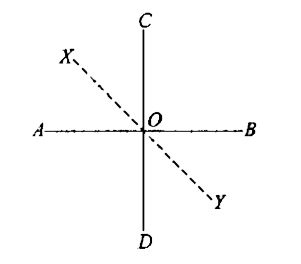
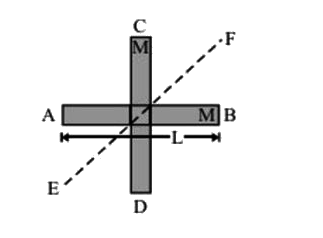
AB and CD are two identical rods each of length l and mass m joined to form a cross. The moment of inertia of these two rods about a bisector (xy) of the angle between the rods is:

mI26
mI23
mI212
2mI23
The correct Answer is:C
Moment of inertia of the combined rods about an axis passing through their point of intersection O and perpendicular to the plane of the rods is
I0=mI212+mI212=mI26
Now xy and are two mutually perpendicular axes passing through O lying in the plane of two rods. Then by symmetry.

IXY=IX'Y'=I (Say)
and IXY+IX'Y'=I0 (from theorem of perpendicular axes).
or 2I=mI26 So, I=mI212
Similar Questions
Knowledge Check
AB and CD are two indential rods each of length L and mass M joined to from a cross. Find the M.L of the system about a bisector of the angel between the rods (XY):
 AML212BML26CML23D4ML23
AML212BML26CML23D4ML23Four thin uniform rods each of length L and mass m are joined to form a square . The moment of inertia of square about an axis along its one diagonal is
AmL26B23mL2C3mL24D4mL23Two uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
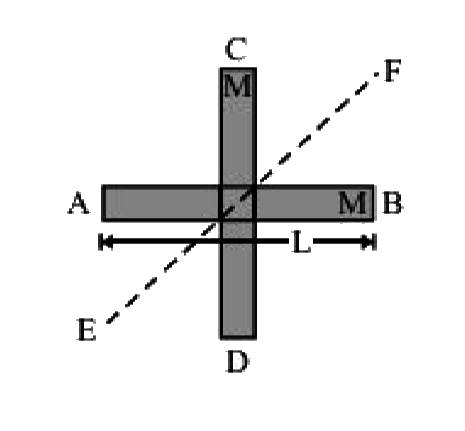 AML26BML24CML212DML23
AML26BML24CML212DML23
four thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View SolutionThree identical thin rods each of length l and mass M are joined together to form a letter H. What is the moment of inertia of the system about one of the sides of H?
View SolutionThree identical thin rods each of length l and mass M are joined together to from a letter H. What is the moment of inertia of the system about one of the sides of H ?
View SolutionTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form as cross as shown. The monent of inertia of the cross about a bisector line EF is
View Solution