Calculate the moment of inertia of the given rod about an axis CD

Moment of inertia of the rod about AB=MI212
using parallel axis theorem
ICD=MI212+M(I4)2=MI212+MI216=748MI2
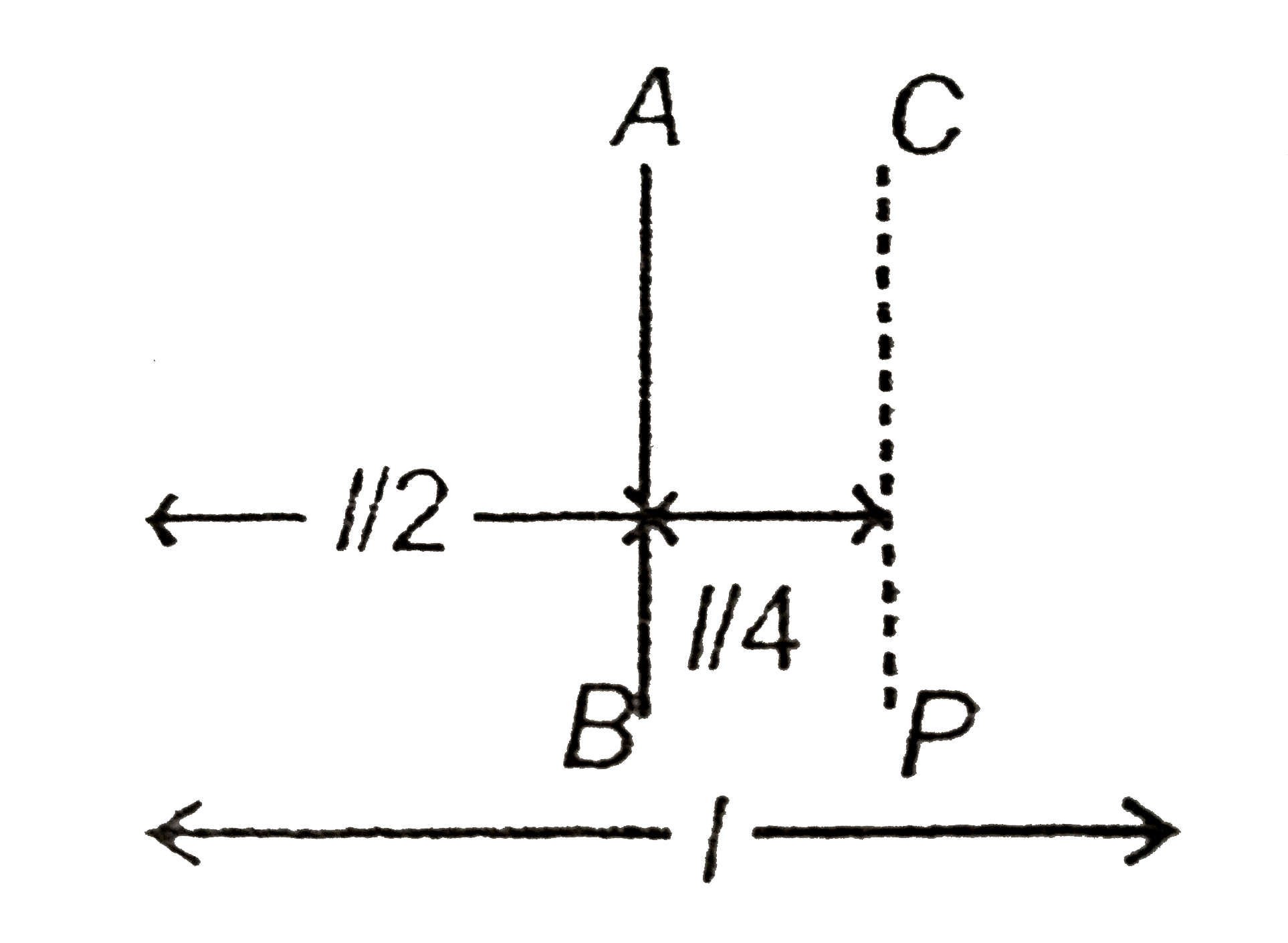
Hint : Use parallel axis theorem.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
Four spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View Solution
Knowledge Check
The moment of inertia of a rod about an axis through its centre and perpendicular to it is 1/12ML² (where M is the mass and L is te length of the rod). The rod is bent in the middle so that the two halves make an angle of 60°. the moment of inertia of the bent rod about the same axis would be
A148ML2B112ML2C124ML2DML28√3The M.I. of a rod about an axis through its center and perpendicular to it is I0. The rod is bent in the middle so that the two halves make an angle θ. The moment of inertia of the bent rod about the same axis would be
AI0sin2θBI0cos2θCI0DI02The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
Calculate the moment of inertia of a thin rod of mass m and length l about a symmetry axis through the centre of mass and perpendicular to the length of the rod, as shown in Fig.
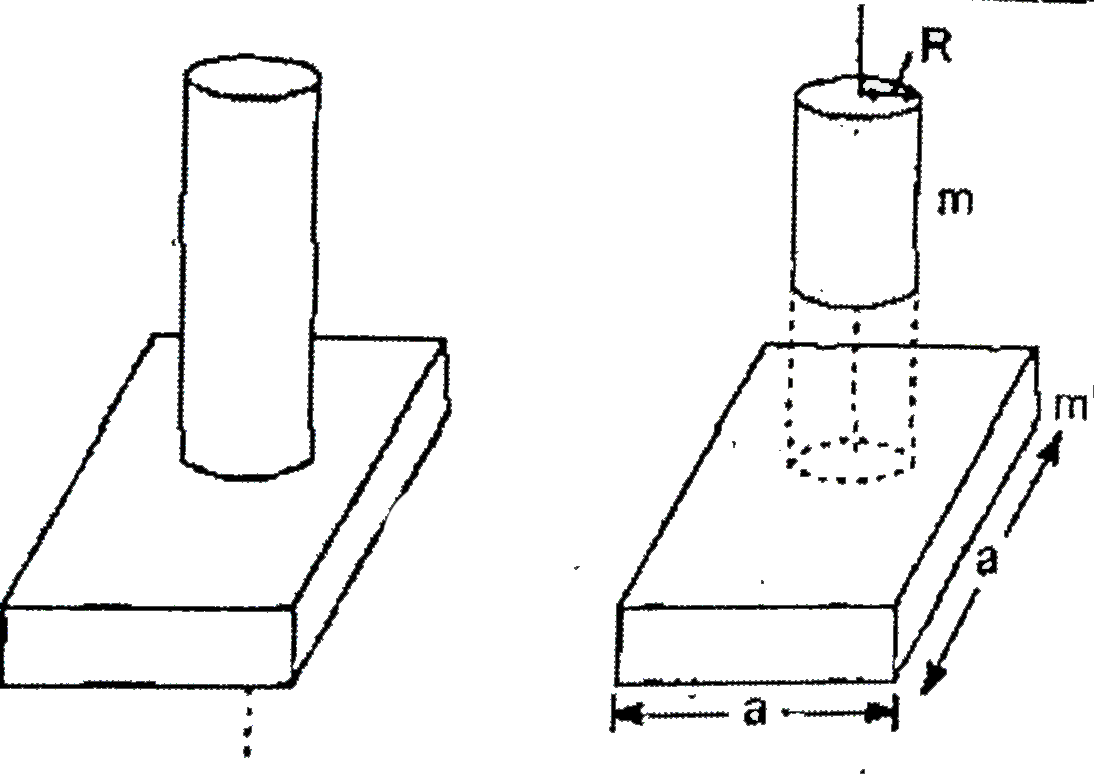
View SolutionThe moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View SolutionThe moment of inertia of a rod about an axis through its centre and perpendicular to it is 112ML2 (where, M is the mass and L is the length of the rod). The rod is bent in the middle so that the two halves make an angle of 60∘ The moment of inertia of the bent rod about the same axis would be :
View SolutionThe moment of inertia of a rod about an axis through its centre and perpendicular to it is 112ML2 (where, M is the mass and L is the length of the rod). The rod is bent in the middle so that the two halves make an angle of 60∘ The moment of inertia of the bent rod about the same axis would be :
View SolutionFigure shows the variation of the moment of inertia of a uniform rod, about an axis passing through itss centre and inclined at an angle θ to the length. The moment of inertia of the rod about an axis passing through one of its ends and making an angle θ=π3 will be
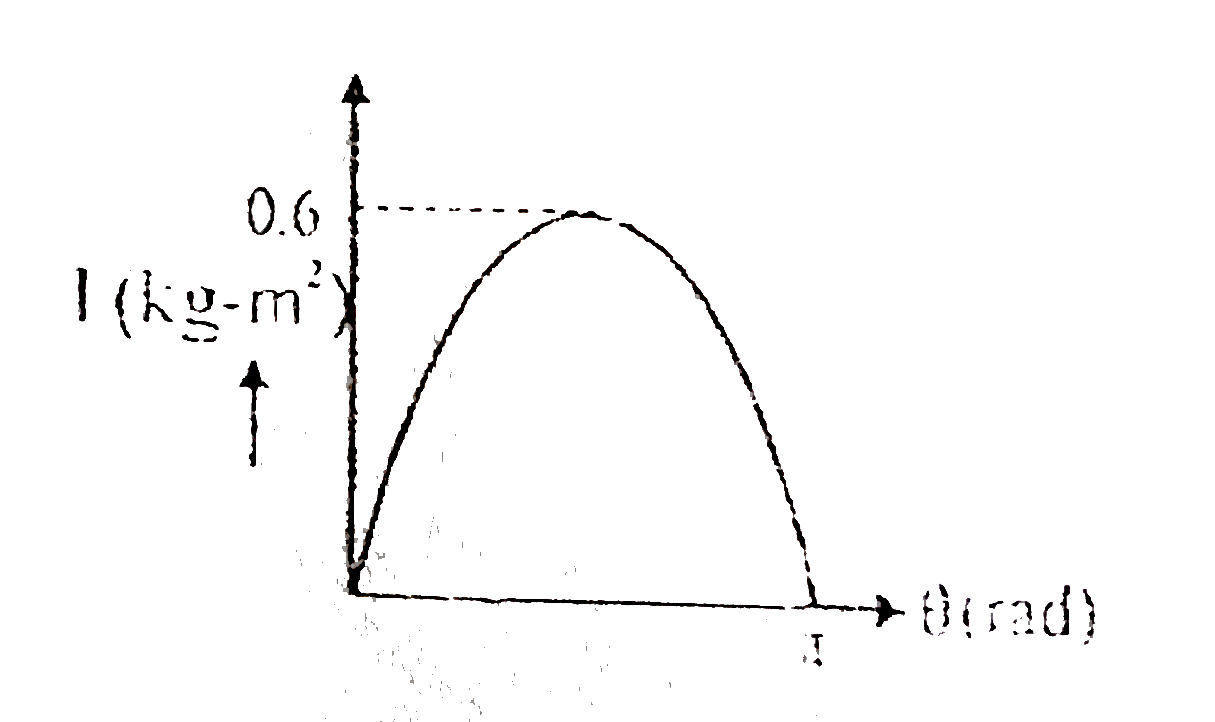
View Solution
