The moment of inertia of a body moving with angular velocity $ω$ decreases from $l$ to $\frac{l}{3}$ without any external torque. Calculate the new angular velocity of the body.

Video Solution

Text Solution

Verified by Experts

$I_{1} ω_{1} = I_{2} ω_{2}$
$ω_{2} = \frac{I_{1} ω_{1}}{I_{2}} = \frac{I ω}{\frac{I}{3}} ⎞ ⎠ = 3 o m \geq a$
Hint : $I_{1} ω_{1} = I_{2} ω_{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION

Topper's Solved these Questions

BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9videos
TEST 1

Similar Questions

Knowledge Check

Question 1 - Select One
If the resultant external torque acting on a body is zero, then angular momentum of the body
Achanges
Bremains constant
Cis infinity
Dzero
Question 2 - Select One
Two points of a rigid body are moving as shown. The angular velocity of the body is :
.
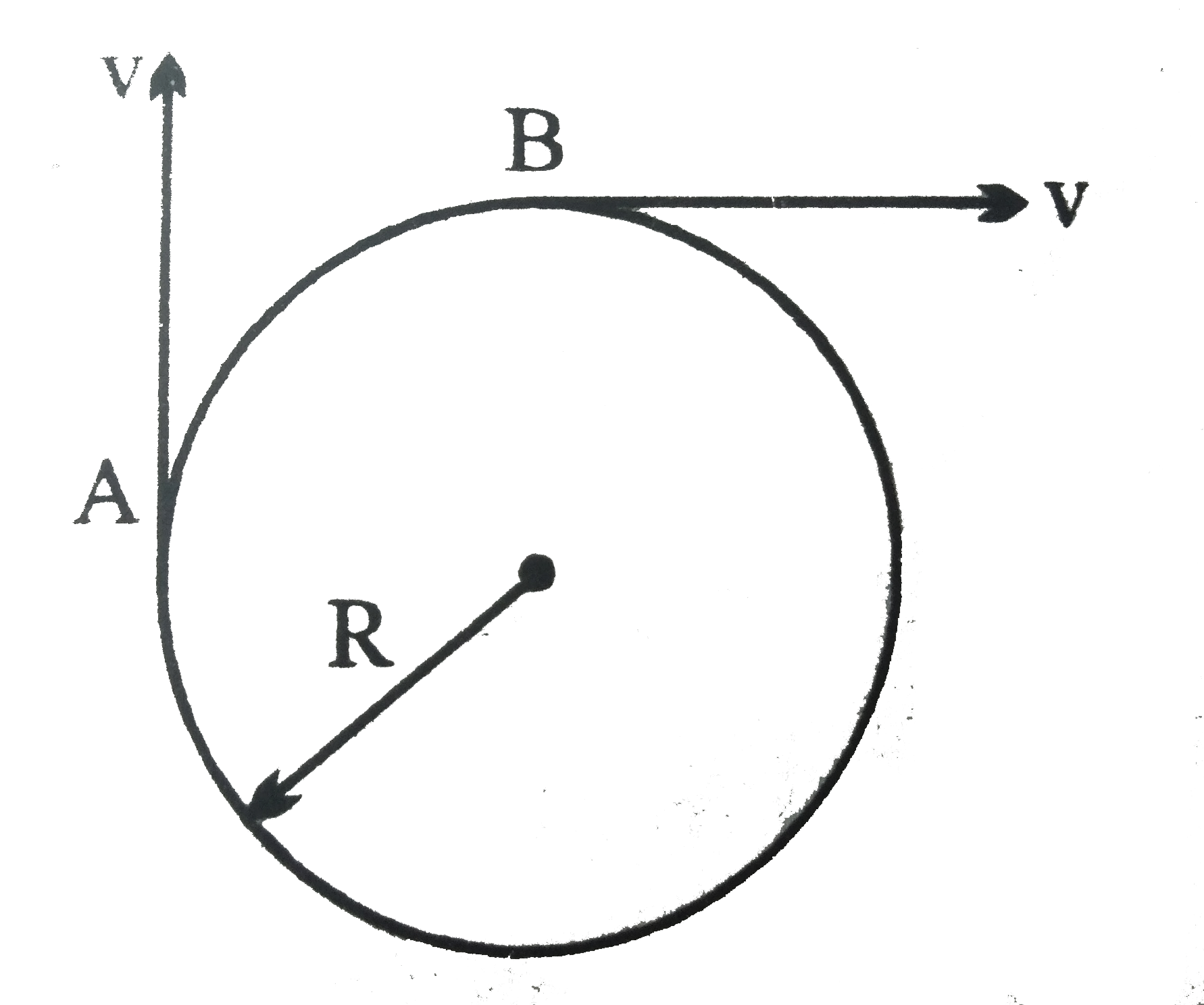A $v / 2 R$
B $v / 2$
C $2 v / R$
D $2 v / 3 R$
Question 3 - Select One
The moment of an inertia about an axis of a body which is rotating with angular velocity ${1rad s}^{- 1}$ is numerically equal to
Aone - fourth of its rotational kinetic energy
Bhalf of the rotational kinetic energy
Crotational kinetic energy
Dtwice the rotational kinetic energy

AAKASH INSTITUTE-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-Try Yourself

Home
Ask Doubt
Profile