A cotton reel of mass m and moment of inertia I is kept at rest on as smooth horizontal surface. The reel has inner and other radius r and R respectively. A horizontal force F starts actings as shown in figure. Find the

a. acceleration of the centre of mass of reel.
b. angular acceleration of the reel
c. net acceleration of point of contact.
a. From force equation F=ma⇒a=F.m……..i
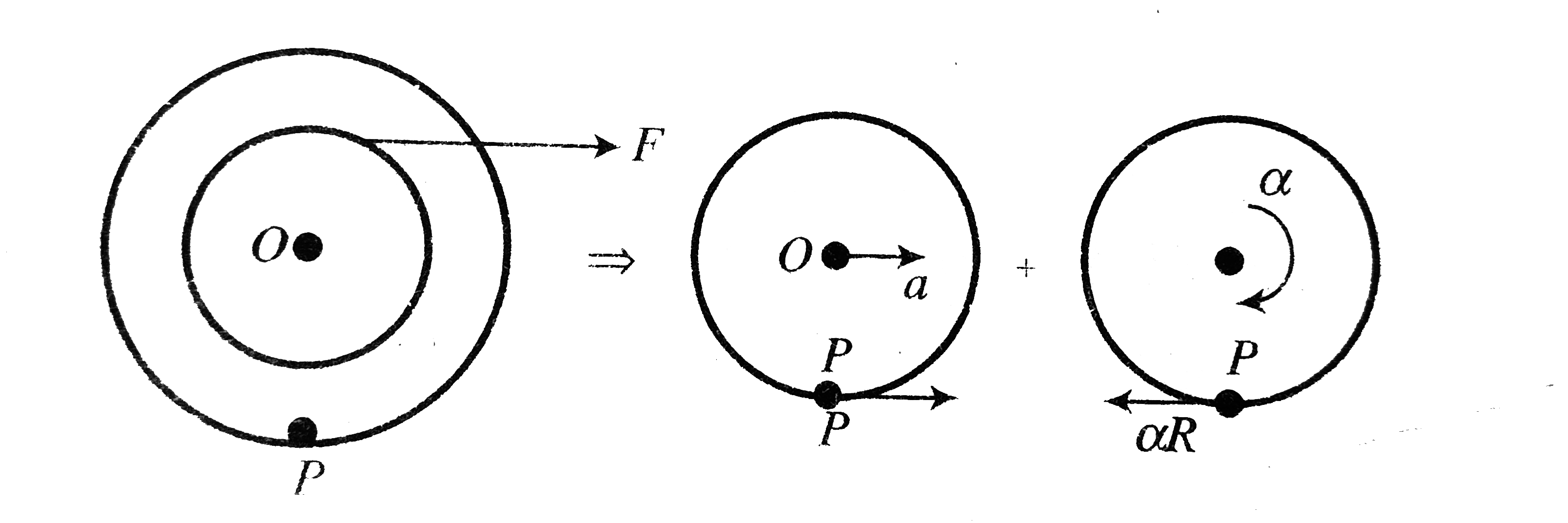
b. We can apply torque equatioinn about centre of mass. From torque equation
Fr=Iα⇒α=FrI……….ii
c. Acceleration of 'P':→aP=→aP,O+→aO
⇒aP=(−αR)+a=a−αR=(a−FrI)R
Hence acceleration of point of contact will be a−(FrI)R in forward direction.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Solved Examples
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A cotton reel of mass m, radius R and moment of inertia I is kept on a smooth horizontal surface. If the string is pulled horizontally by a force F, find the (i) acceleration of CM, (ii) angular acceleration of the cotton reel.

View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
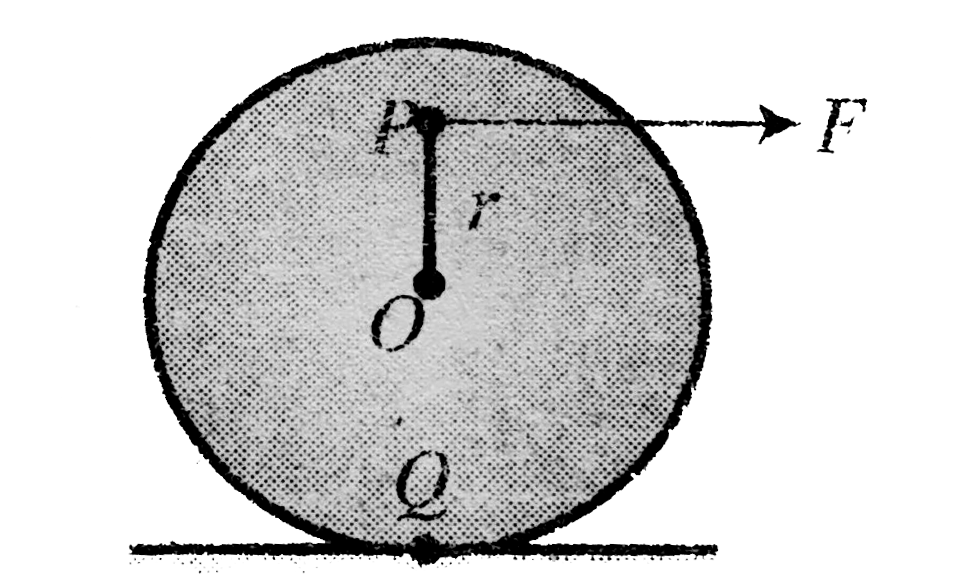
angular acceleration of the disc. (rads−1)
View Solution
Knowledge Check
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound isAzeroBω2RCaD√a2+(ω2R)2A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
Ah=RBh=2RCh=0Dthe acceleration will be same whatever h may be
A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
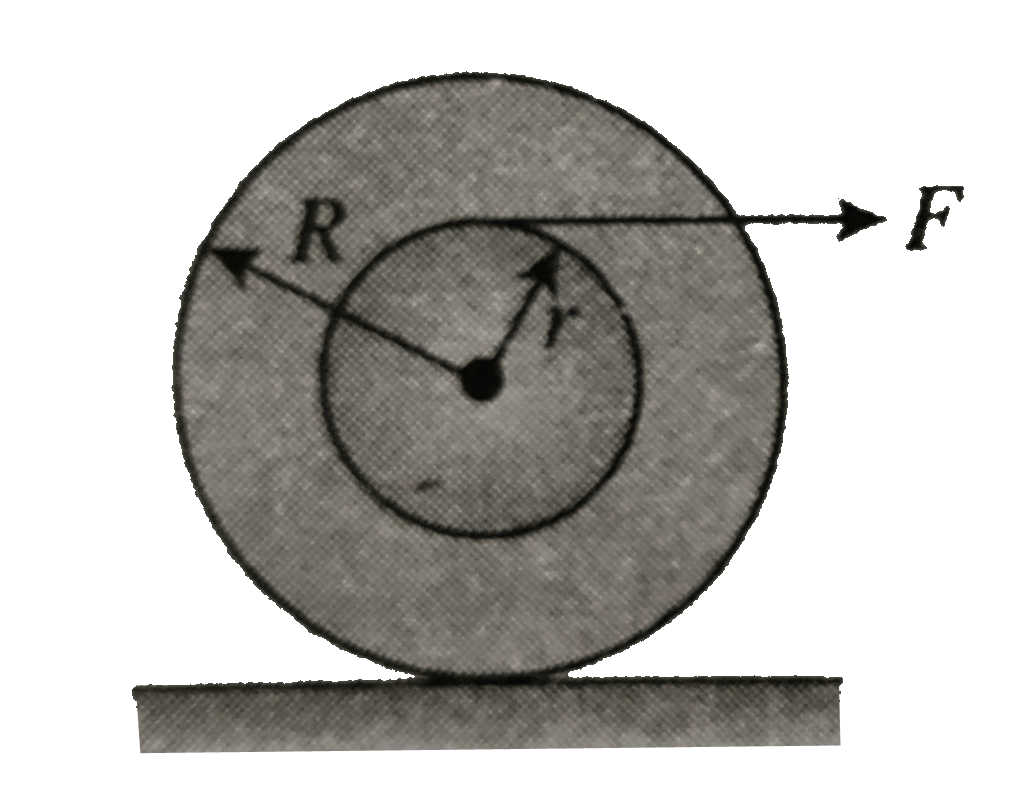
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:

acceleration of the CM (in ms2)
View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

View SolutionConsider a system of two identical particles. One of the particls is at rest and the other has an acceleration.The centre of mass has an acceleration vaca The centre of mass has an acceleration.
View Solution

