A parallel beam of particles of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
2mnv2cosθ
2mnv2cos2θ
2mnvcosθ
2mnvcos2θ
The correct Answer is:B
The change number of particle n volume dvsdxisdN=ndv=ndsx
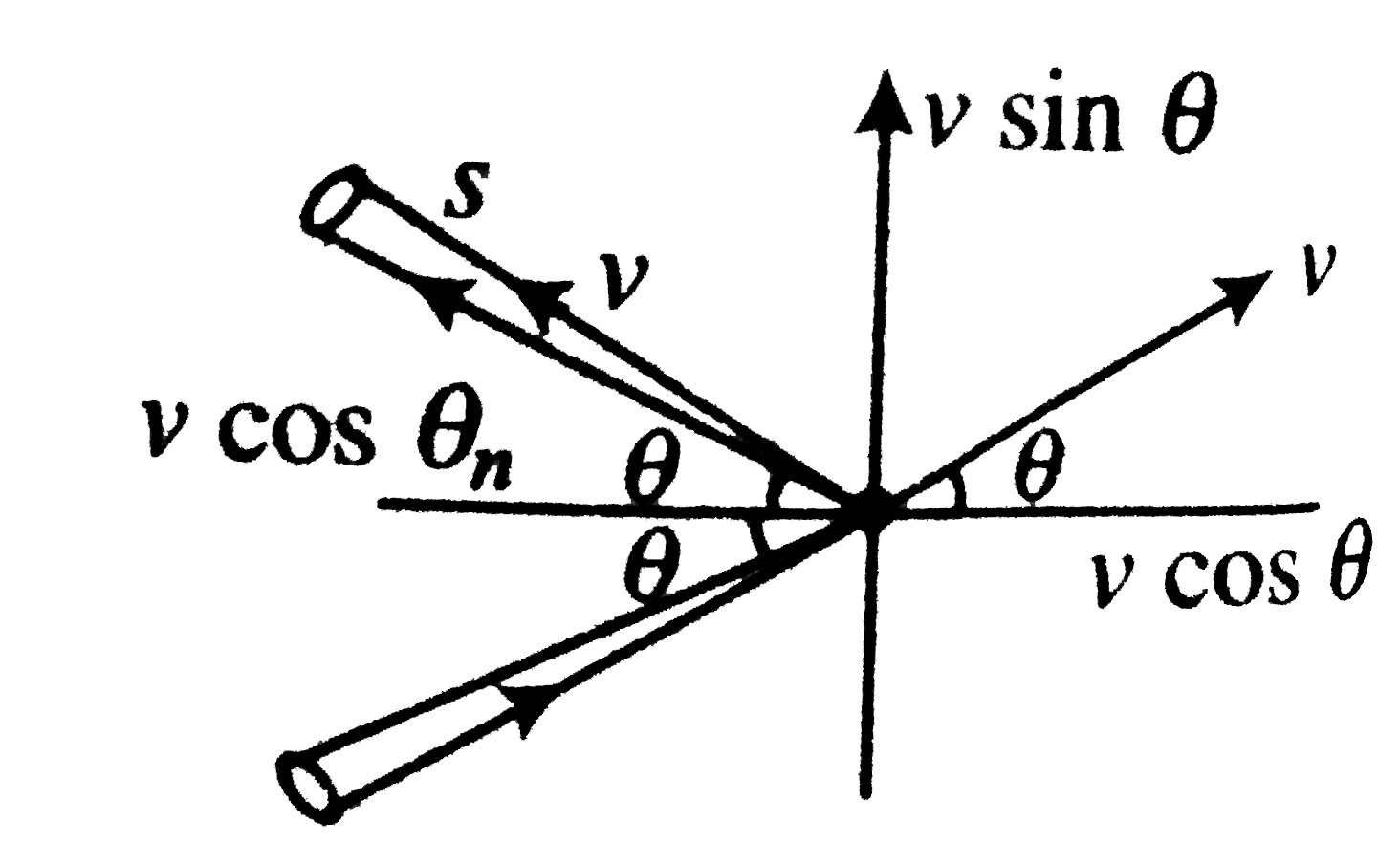
∴Dm=mdN=mnsdx
∴dmdt=mnsdxdt=mnsv
: F=dpdt=△vdmdt
F(2vcosθ)mnsv
F−2mnv2scosθ
∴ pressure p=→F.→ss2
p=Fscosθs2=Fcosθs=2mnv2cos2θ
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A parallel beam of molecules moving with velocity v impinges on a wall at an angle θ to its normal. Find the pressure exerted by the beam on the wall assuming perfect elastic collisions. The concentration of the molecules in the beam is n.
View SolutionA parallel beam of nitrogen molecules moving with velocity v=400ms−1 imprings on a wall at an angle θ=30∘ to its normal. The concentration of molecules in the beam is n=9×1018cm−3. Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.
View Solution
Knowledge Check
A molecule of mass m moving at a velocity v impinges elastically on the wall at an angle a with the wall. Then
Athe impulsive reaction of the wall is 2mvcosαBthe impulsive reaction of the wall is 2mvsinαCthe impulsive reaction of the wall is nonzeroDgiven data is insufficient to calculate impulsive reaction of the walln bullets per sec each of mass m moving with velocity v strike normally on a wall. The collision is elastic then force on wall is-
AzeroBmnvC2 mnvD4 mnvA molecule of mass m moving with a velocity v makes 5 elastic collisions with a wall of the container per second. The change in its momentum per second will be
AmvB5 mvCmv10D10 mv
A stream of particles each of mass m moving with velocity v with number of particles per unit volume n strike against a wall at an angle θ to the normal elastically. Find the pressure exerted by the exerted by the stream on the wall.
View SolutionA particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
View SolutionA particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
View Solution

