Three particles of equal masses are placed at the corners of an equilateral triangle as shown in the figure. Now particle A starts with a velocity v1 towards line AB, particle B starts with a velocity v2 towards line BC and particle C starts with velocity v3 towards line CA. The displacement of CM of three particle A,B and C after time t will be (given if v1=v2=v3)

zero
v1+v2+v33t
v1+√32v2+v323t
v1+v2+v34t
The correct Answer is:A
Using →vCM=ˆivx+ˆjvy
where vx=mv(x)1+mv(x)2+mv(x)23m=0
vy=mvy1+mvy2=mvx33m=0
net velocity of zero (using vector theory) i.e. CM is at rest. So, displcement of CM of zero. So choices b,c and d are wrong.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Let there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v1 towards line AB, particle B starts with the velocity v2, towards line BC and particle C starts with velocity v3 towards line CA. Find the displacement of the centre of mass of the three particles A,B and C after time t. What would it be if v1=v2=v3?
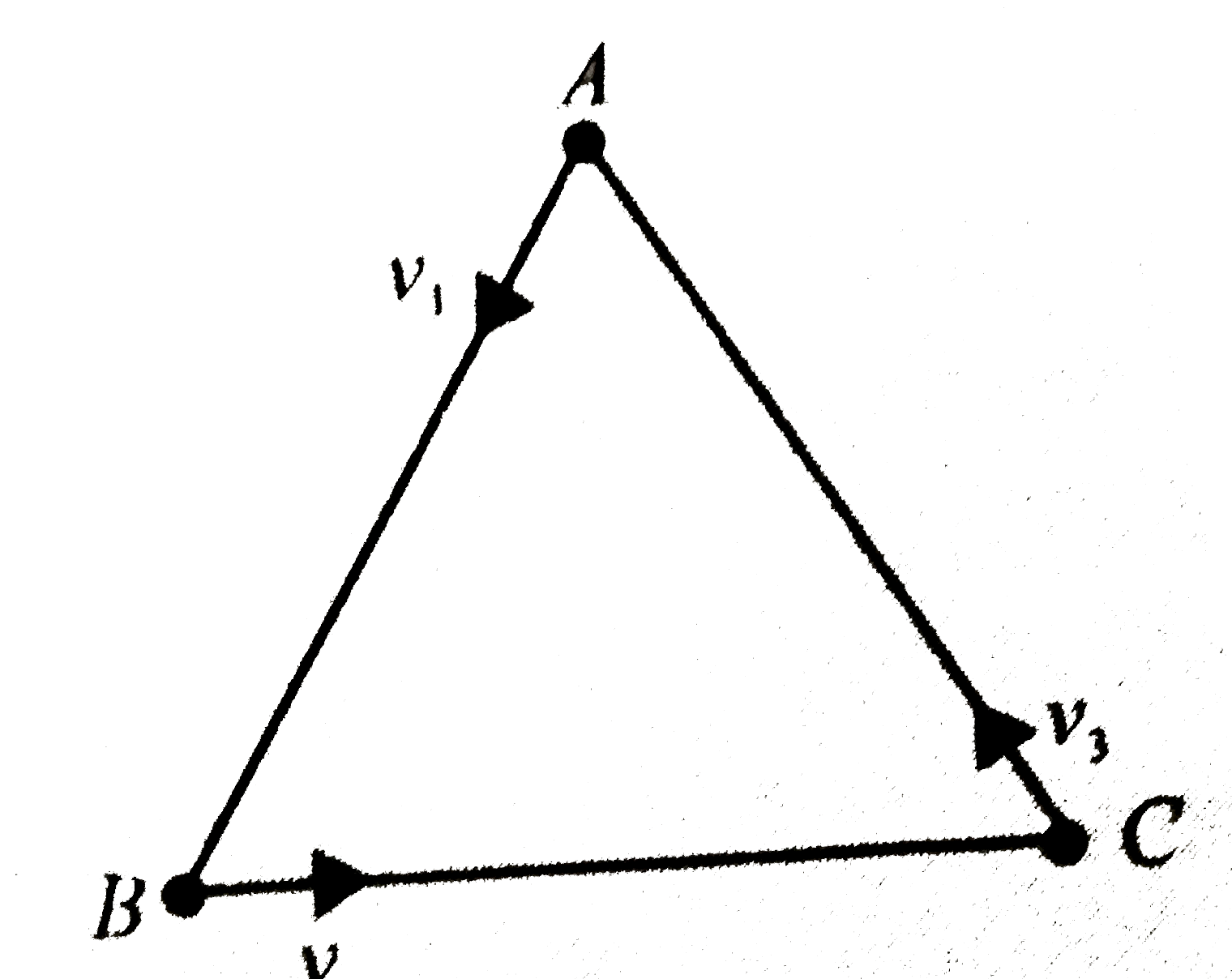
View SolutionThree particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
View Solution
Knowledge Check
Three particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
 AAwrt.Bis=vcos30∘a in z-directionBBwrt.Cis=vcos30∘a in z-directionCAwrt.Cis=vcos30∘a in z-directionDBwrt.Ais=vcos30∘a in z-direction
AAwrt.Bis=vcos30∘a in z-directionBBwrt.Cis=vcos30∘a in z-directionCAwrt.Cis=vcos30∘a in z-directionDBwrt.Ais=vcos30∘a in z-directionA particle of mass m has a velocity −v0i, while a second particle of same mass has a velocity v0j. After the particles collide, first particle is found to have a velocity −12v0¯i then the velocity of othe particle is
A−12v0→i+v0→jB12v0→i+v0→jCv0→i+v0→jD−v0→i+v0→jA particle starts from rest with uniform acceleration a. Its velocity after n seconds is v. The displacement of the particle in the two seconds is :
A2v(n−1)nBv(n−1)nCv(n+1)nD2v(2n+1)n
A particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionA particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
View SolutionA particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
View SolutionA particle moves with an initial velocity v0 and retardation αv, where v is the velocity at any time t.
View Solution
