A mass $m_{1}$ moves with a great velocity. It strikes another mass $m_{2}$ at rest in head-on collision. It comes back along its path with low speed after collision. Then

$m_{1} > m_{2}$

$m_{1} < m_{2}$

$m_{1} = m_{2}$

there is no relation between $m_{1}$ and $m_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

The sphere $A$ of mass $m_{1}$ moves with velocity $V$ on a frictionless horizontal surface and strikes with sphere $B$ of mass $m_{2}$ at rest. The sphere $A$ comes back with speed $V / 10$ . Choose the correct option.

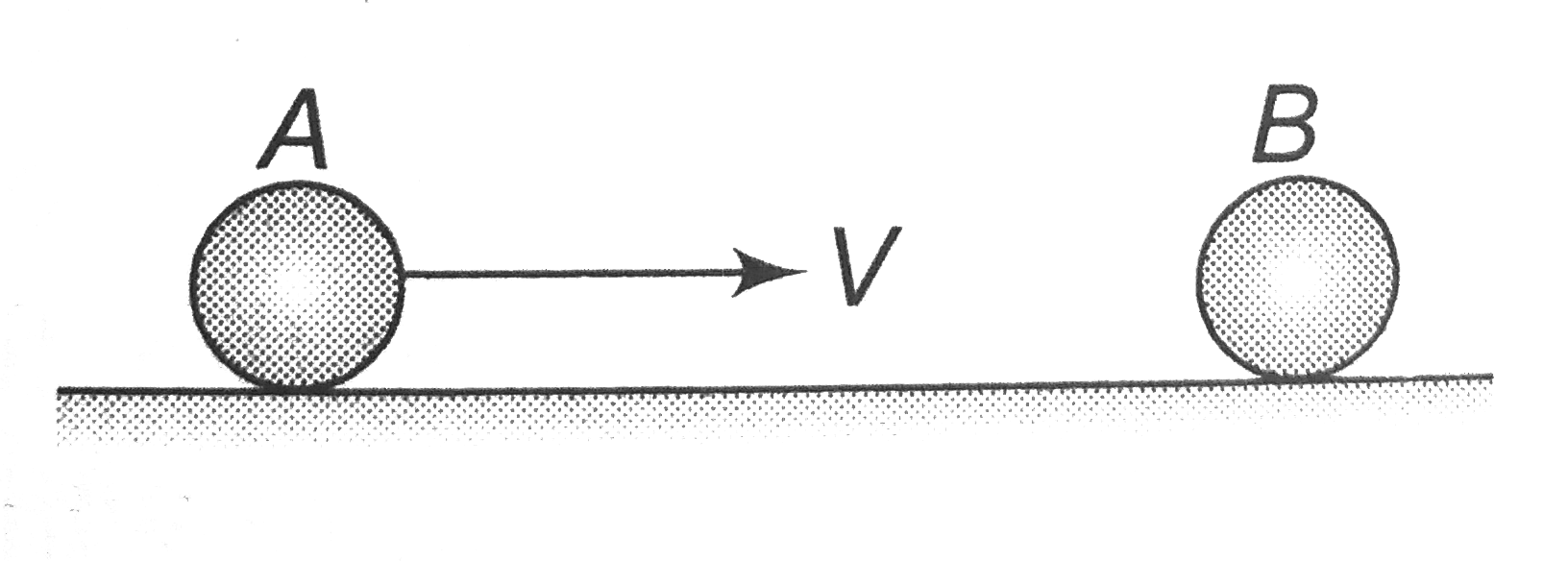A $m_{1} > m_{2}$
B $m_{1} = m_{2}$
C $m_{1} < m_{2}$
Dnone of these
Body A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
A $\frac{5}{9}$
B $\frac{1}{9}$
C $\frac{8}{9}$
D $\frac{4}{9}$
Body A of mass 4 m moving with speed u collides with another body B of mass 2m, at rest. The collision is head on and elastic in nature. After the collision the fraction of energy lost by the colliding body A is
A $5 / 9$
B $1 / 9$
C $8 / 9$
D $4 / 9$