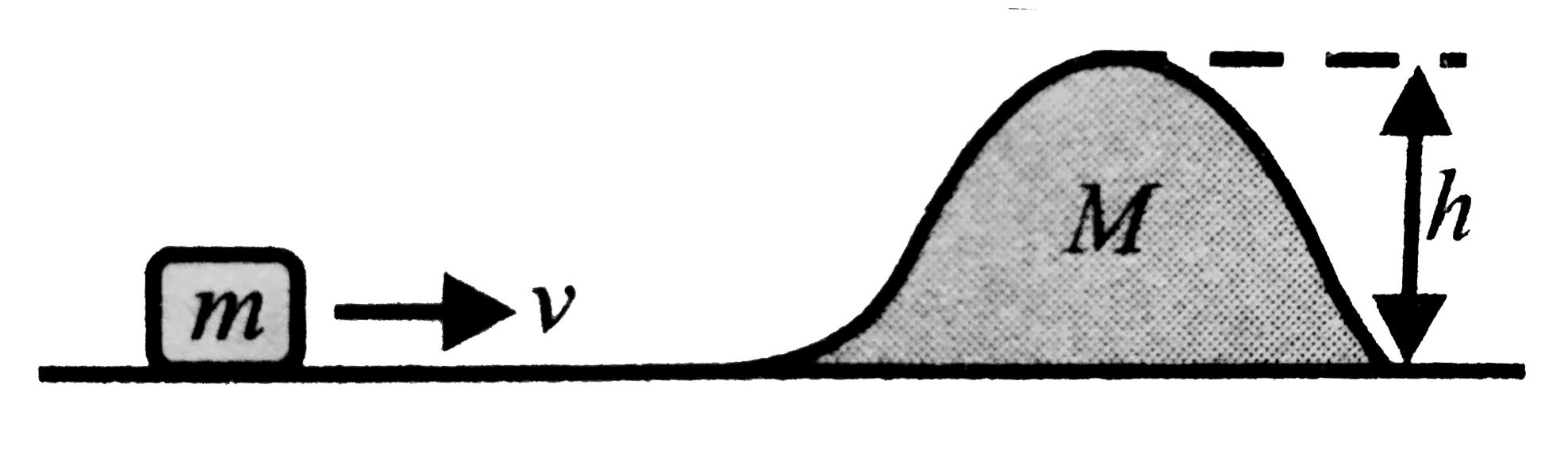
For the system shown in the figure, a small block of mass m and smooth irregular shaped block of mass M, both free to move are placed on a smooth horizontal plane. The
minimum velocity v imparted to block so that it will overcome the highest point of M is
√2gh
√2(1+mM)gh
√2mMgh
√2(1+Mm)gh
The correct Answer is:B
For the given situation, block should be able to reach just at highest point of M, and their relative velocity is to become zero. Let their common velocity of vC.
COLM→(M+m)vC=mv⇒vC=mvM+m
COME:12(M+m)v2C+mgh=12mv2
Solve to get v=√2(1+mM)gh
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Knowledge Check
Figure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
What minimum velocity should be imparted to a small block of same mass m so that it may each point B :
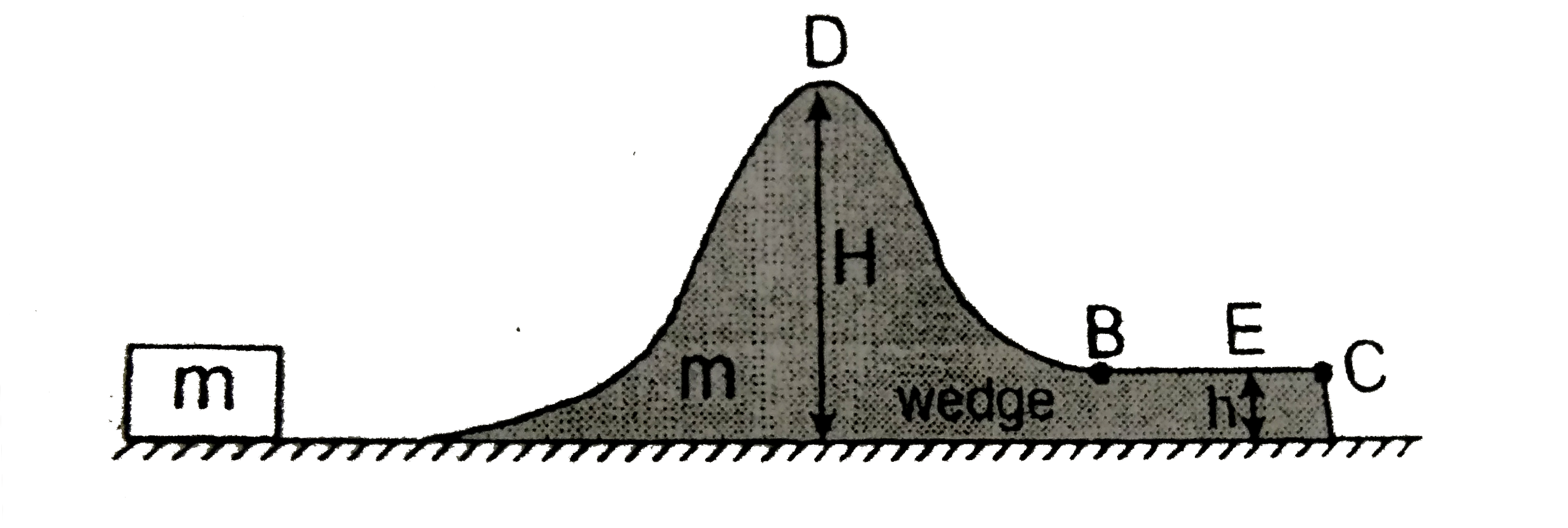 A2√gHB√2gHC2√g(H−h)D√gh
A2√gHB√2gHC2√g(H−h)D√ghA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the aboveA block of mass m is placed gently onto a long plank of mass M moving with a velocity v0 on a smooth horizontal floor. If friction is present between M and m :
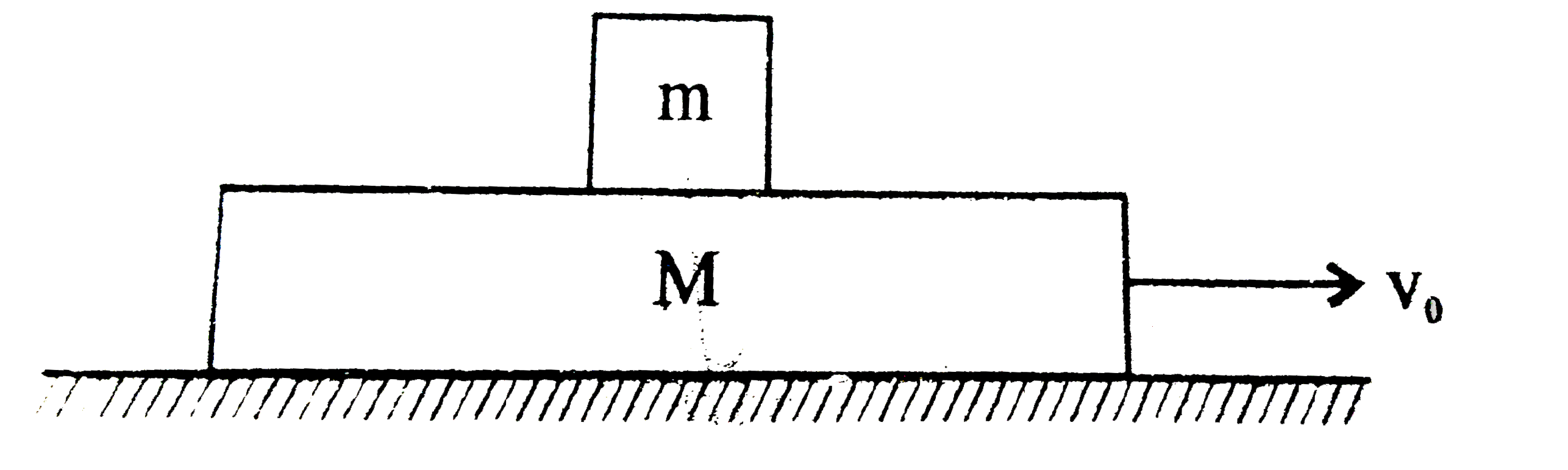 Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
In the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.

View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

View SolutionBlock A of mass m is placed over a wedge of same mass m. Both the block and wedge are placed on a fixed inclined plane. Assuming all surfaces to be smooth calculate the displacement of the block A in ground frame in 1s.
View SolutionThe figure shows a block of mass M=2m having a spherical smooth cavity of radius R placed on a smooth horizontal surface .There is a small ball of mass m moving at an instant vertically downward with a velocity v with respect to the block .At this instant :

View Solution