A parallel beam of nitrogen molecules moving with velocity v=400ms−1 imprings on a wall at an angle θ=30∘ to its normal. The concentration of molecules in the beam is n=9×1018cm−3. Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.
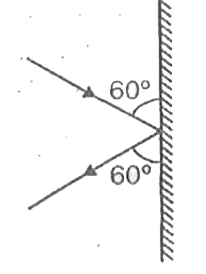
All the molecules contained in the cylinder of length v and inclined on the wall at an angle θ to the normal will strike the wall every second. Let Δ S be the base area of the cylinder.
The volume of the cylinder =ΔSvcosθ.
Therefore, the number of molecules striking ΔS every second =(ΔSvcosθ×n).
Change of momentum per molecule =2mvcosθ.
∴Pressure=ForceArea=(2mvcosθ)(ΔSvcosθ×n)(ΔScos2θ)=2mv2n
∴p=2×(286.0×1026)(9×1024)×4002×cos230∘
=1.00×105Nm−2=1 atm

Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Solved Examples
Explore 14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.1
Explore 20 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
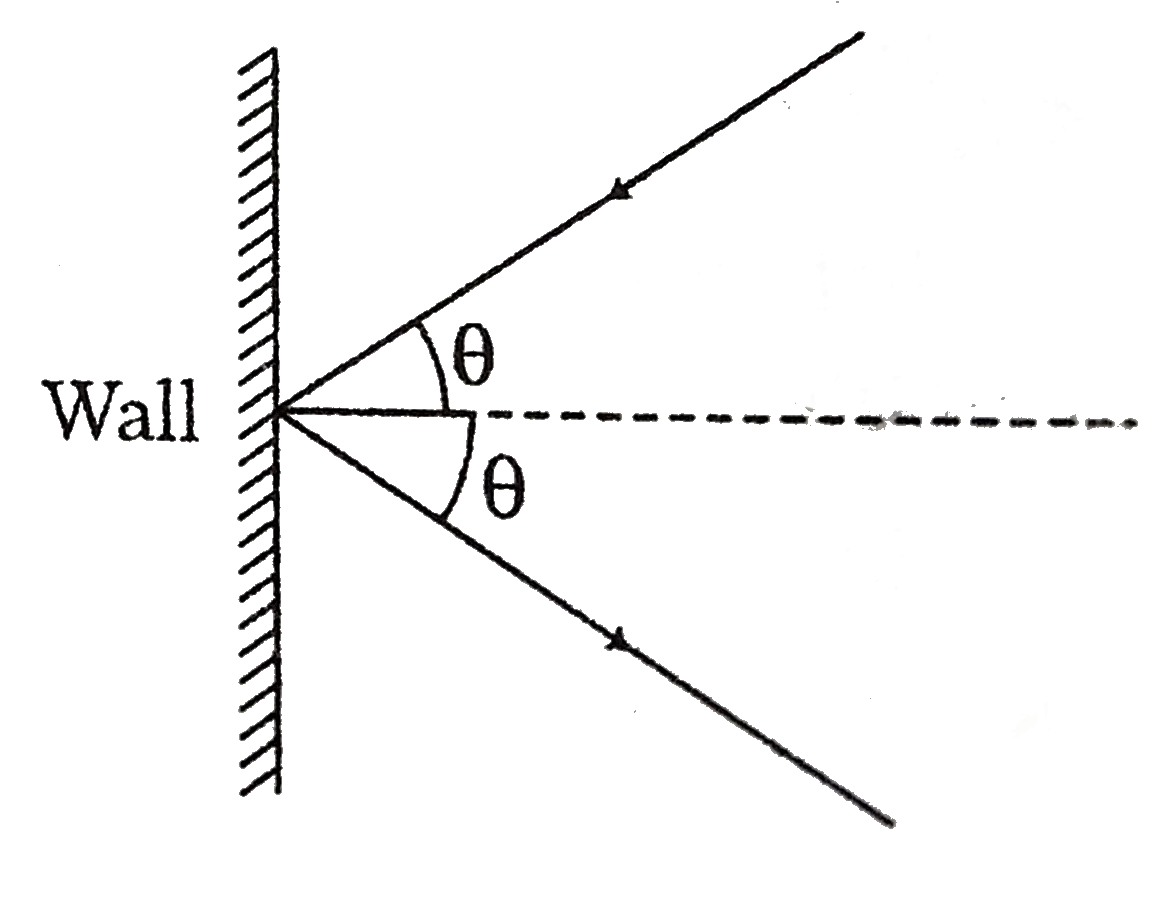
A parallel beam of molecules moving with velocity v impinges on a wall at an angle θ to its normal. Find the pressure exerted by the beam on the wall assuming perfect elastic collisions. The concentration of the molecules in the beam is n.
View SolutionA stream of particles each of mass m moving with velocity v with number of particles per unit volume n strike against a wall at an angle θ to the normal elastically. Find the pressure exerted by the exerted by the stream on the wall.
View Solution
Knowledge Check
A parallel beam of particles of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
A2mnv2cosθB2mnv2cos2θC2mnvcosθD2mnvcos2θA molecule of mass m moving with a velocity v makes 5 elastic collisions with a wall of the container per second. The change in its momentum per second will be
AmvB5 mvCmv10D10 mv1023 molecules of a gas, each having a mass of 3×10−27 kg strike per second per sq. cm. of a rigid will at an angle of 60∘ with the normal and rebound with a velocity of 500m/s. What is the pressure exerted by the gas molecules on the wall?
A500N/m2B1000N/m2C1500N/m2D2000N/m2
The mass of hydrogen molecule is 3.23×1023 hydrogen molecules strike 2cm2 of a wall per second at an angle of 45∘ with the normal when moving with a speed of 105cms−1, what pressure do they exert on the wall ? Assume collision to be elasitc.
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
View SolutionA beam of helium atoms moves with a velocity of 2×103ms−1. Find the wavelength associated with helium atoms.
View SolutionThe density of a gas is 6×10−2kg/m3 and the root mean square velocity of the gas molecules is 500 m/s. The pressure exerted by the gas on the walls of the vessel is
View SolutionThe mass of hydrogen molecule is 3.32×10−27 kg. If 1023 hydrogen molecules strick per second at 2 cm2 area of a rigid wall at an angle of 45∘ from the normal and rebound back with a speed of 1000 ms−1, then the pressure ezxeted on the wass is
View Solution

