Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
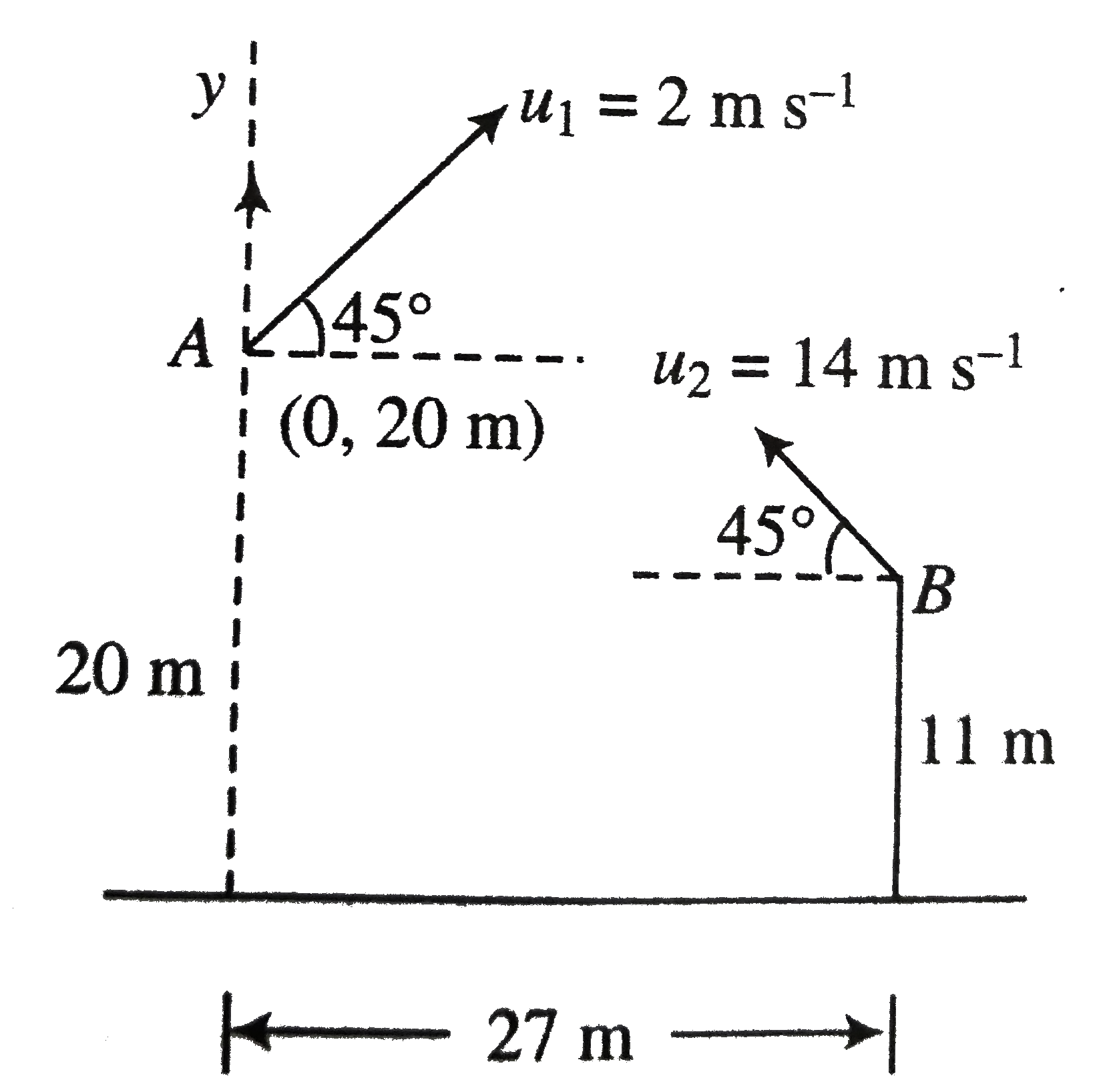
The direction (angle) with horizontal at which B will appear to move as seen from A is
37∘
53∘
15∘
90∘
The correct Answer is:B
b. tanϕ=6√28√2⇒tanϕ=34⇒ϕ=37∘ .
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type
17 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Two particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionTwo bodies A and B are projected simultaneously from points X and Y as shown in the figure, with velocities uA and uB respectively.

Find the ratio of uAuB for both the bodies to collide .
View Solution
Knowledge Check
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
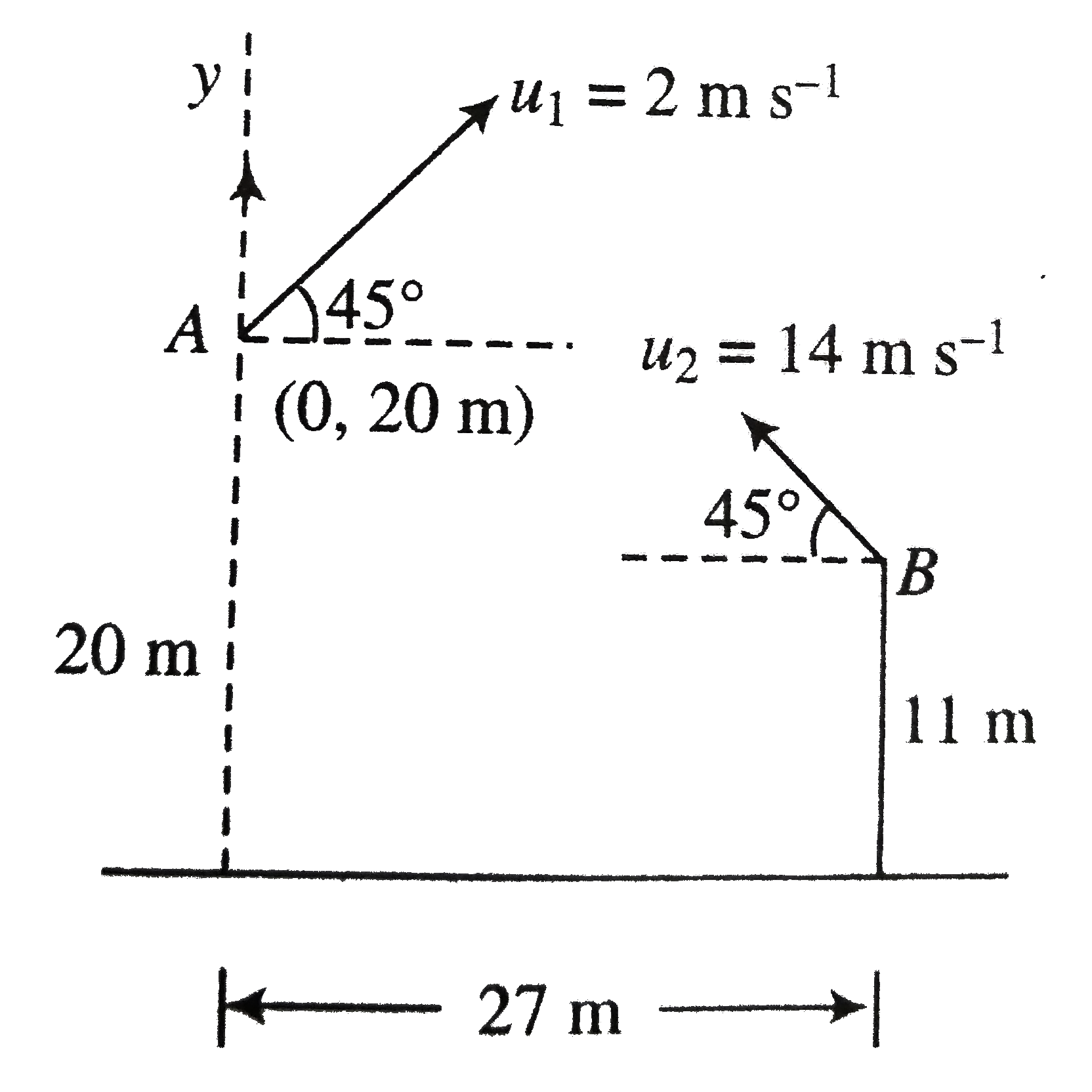
Minimum separation between A and B isA3 mB6 mC12 mD9 mTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
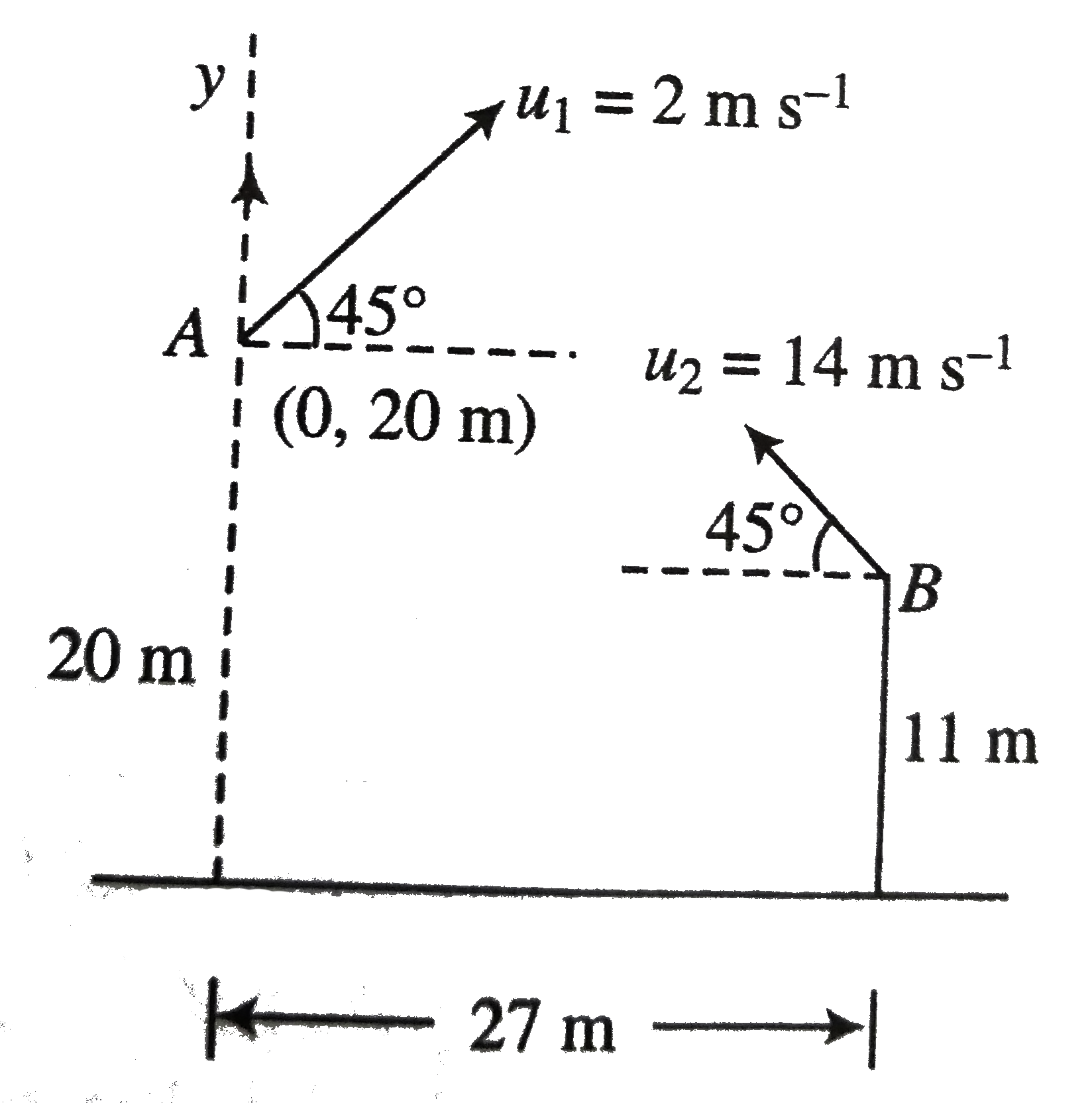
The relative velocity of B as seen from A inA−8√2ˆi+6(√2)ˆjB4√2ˆi+3(√3)ˆjC3√5ˆi+2(√3)ˆjD3√2ˆi+4(√3)ˆjTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then
 Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
Two particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionTwo particles move in a uniform gravitational field with an acceleration g.At the initial moment the particles were located at same point and moved with velocities u1=9ms−1 and u2=4ms−1 horizontally in opposite directions.The time between the particles at the moment when their velocity vectors are mutually perpendicular in s in (take g=10ms−2)
View SolutionTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
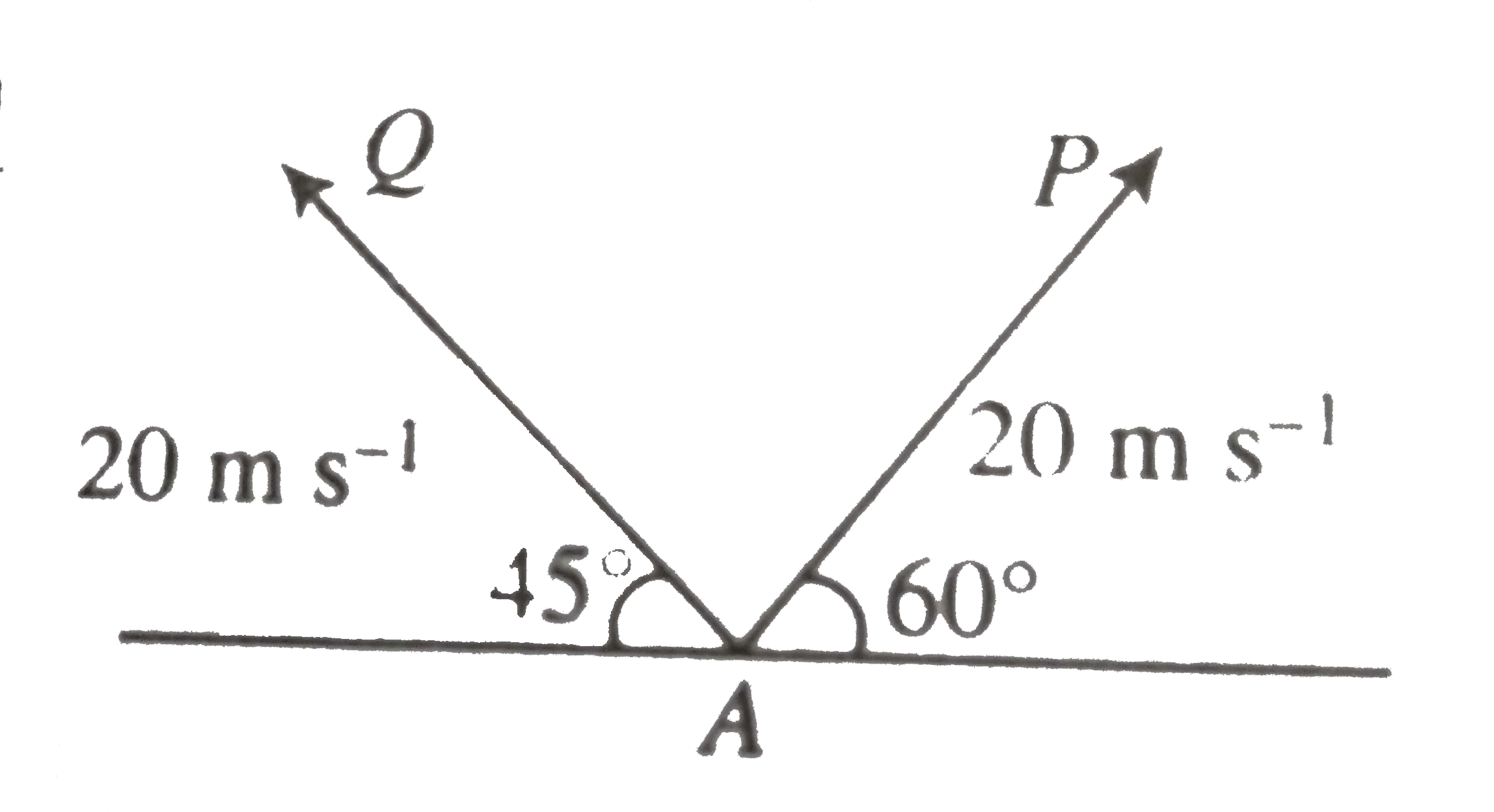
View SolutionTwo particles are projected simultaneously in the same vertical plane, from the with speed u1 and u2 at angle of projection θ1 and θ2 respectively with the horizontal. The path followed by one, as seen by other (as long as both are in flight), is
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil be
View Solution
