Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
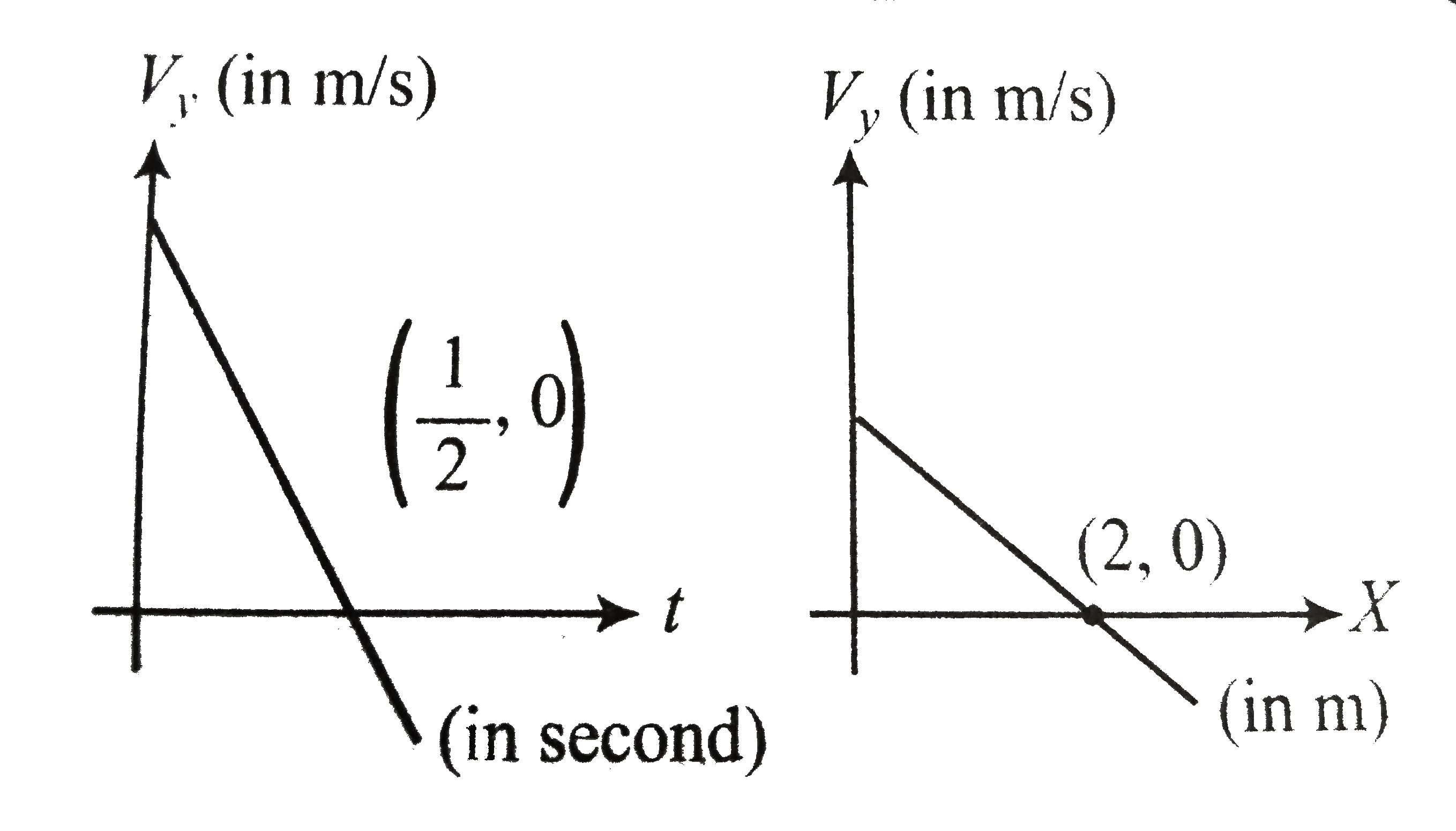 ,
,
The projection speed is :
√37ms−1
√41ms−1
√14ms−1
√40ms−1
The correct Answer is:B
Time of flight (T) = 1s
2uyg=1s⇒uy=5ms−1
Range (R) = 4m.
2(ux)(uy).g=4⇒ux=4ms−1
u=√u2x+u2y=√41ms−1
θ=tan−1(uyux)=tan−1(54)
H=u2y2g=(5)220=54=1.25m.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type
17 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Two graphs of the same projectile motion (in the x - y plane) projected from origin are shown in (Fig. 5 .10). X - axis is along horozontal direction and Y - axis is vertically upwards. Take g=10ms2
Find (i) The y component of initial velocity and
(ii) the X component of initial velocity.
 .
.
View SolutionA projectile is thrown from ground at a speed v0 at an angle α to the horizontal. Consider point of projection as origin, horizontal direction as X axis and vertically upward as Y axis. Let t be the time when the velocity vector of the projectile becomes perpendicular to its position vector.
(a) Write a quadratic equation in t.
(b) What is the maximum angle a for which the distance of projectile from the point of projection always keeps on increasing? [Hint: Start from the equation you obtained in part (a)]
View Solution
Knowledge Check
Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
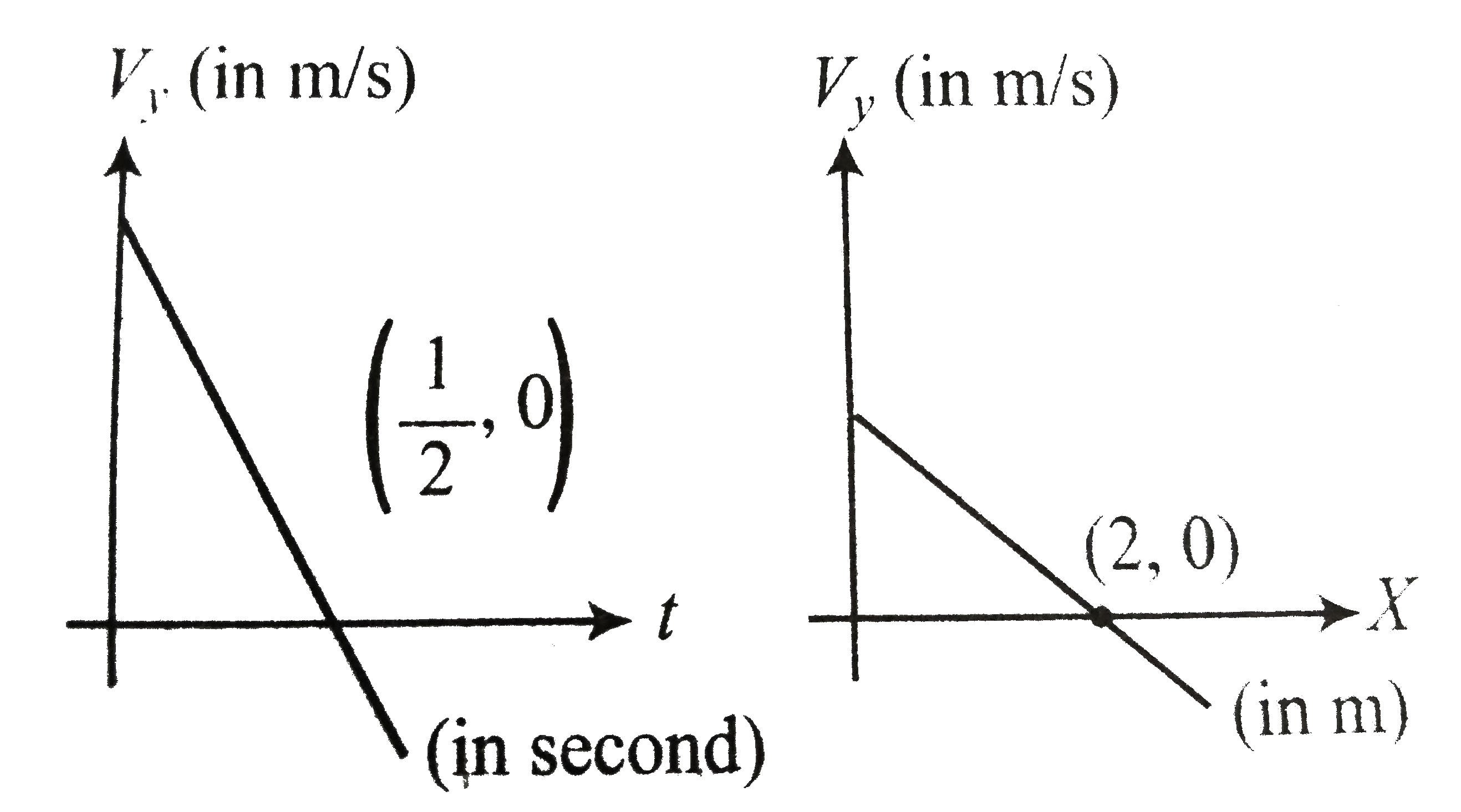
Projection angle with the horizontal is :Atan−1(45)Btan−1(23)Ctan−1(54)Dtan−1(12)Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
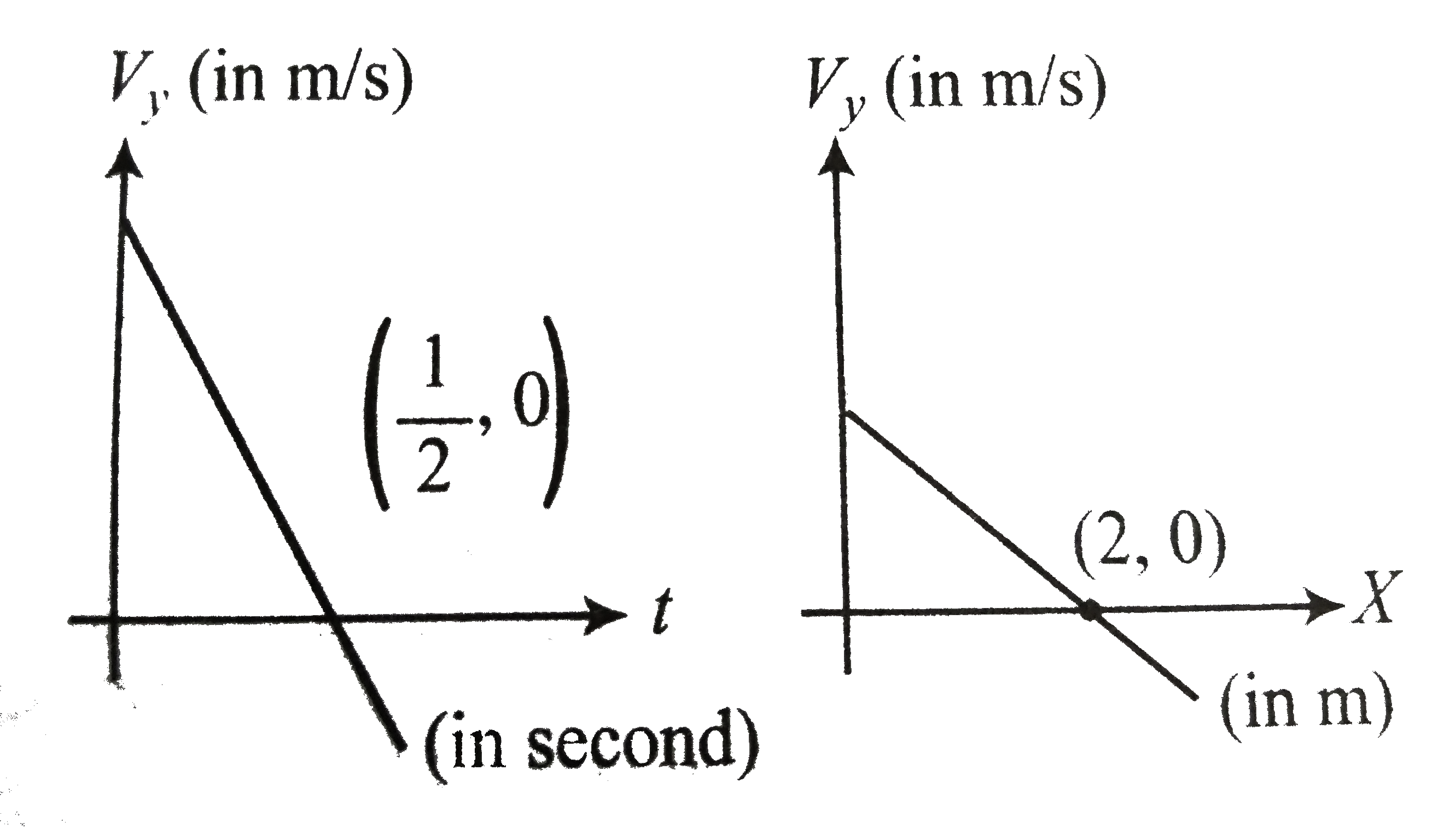 ,
,
Maximum height attained from the point of projection isA1.25 mB12.5 mC2.25 mDNone of theseA particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
A45∘B60∘C30∘Dtan−1(3/4)
For shown situation draw a graph showing accelerations of A and B on y-axis and time of x-axis. (g=10ms−2)
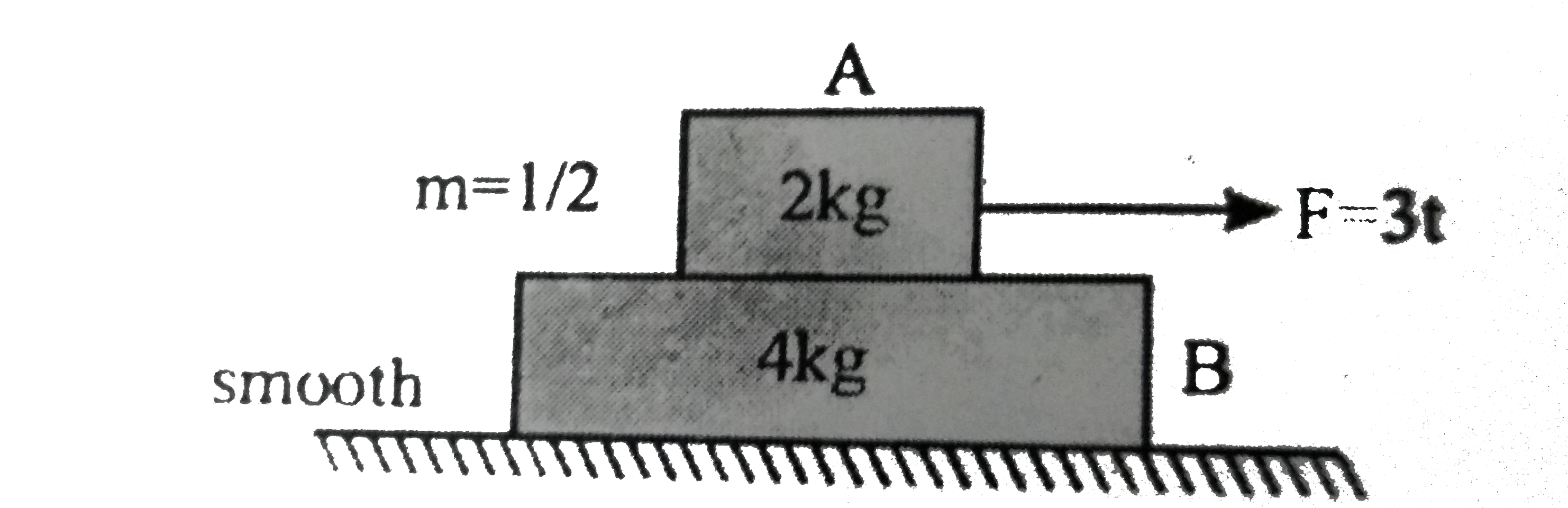
View SolutionAt a height of 0.4 m from the ground, the velocity of projectile in vector from is →u=(6ˆi+2ˆj) (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is : (g=10m/s2)
View SolutionA bullet is fired from horizontal ground at some angle passes through the point, where R is the range of the bullet. Assume point of the fire to be origin and the bullet moves in x-y plane with x-axis horizontal and y-axis vertically upwards. Then angle of projection is
View Solution
A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:
View SolutionMatch the following

A particle is projected from a large fixed incline plane as shown. Here (Vertically downward) take g=10m/s2.
View Solution
