We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

${\vec{v}}_{b o a t} = {\vec{v}}_{b o a t, w a t e r} + {\vec{v}}_{w a t e r}$ .
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.

$u {(\frac{3 d}{5})}^{1 / 3}$

$u {(\frac{3 d}{5})}^{1 / 3}$ + 1

$u {(\frac{6 d}{5})}^{1 / 3}$

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

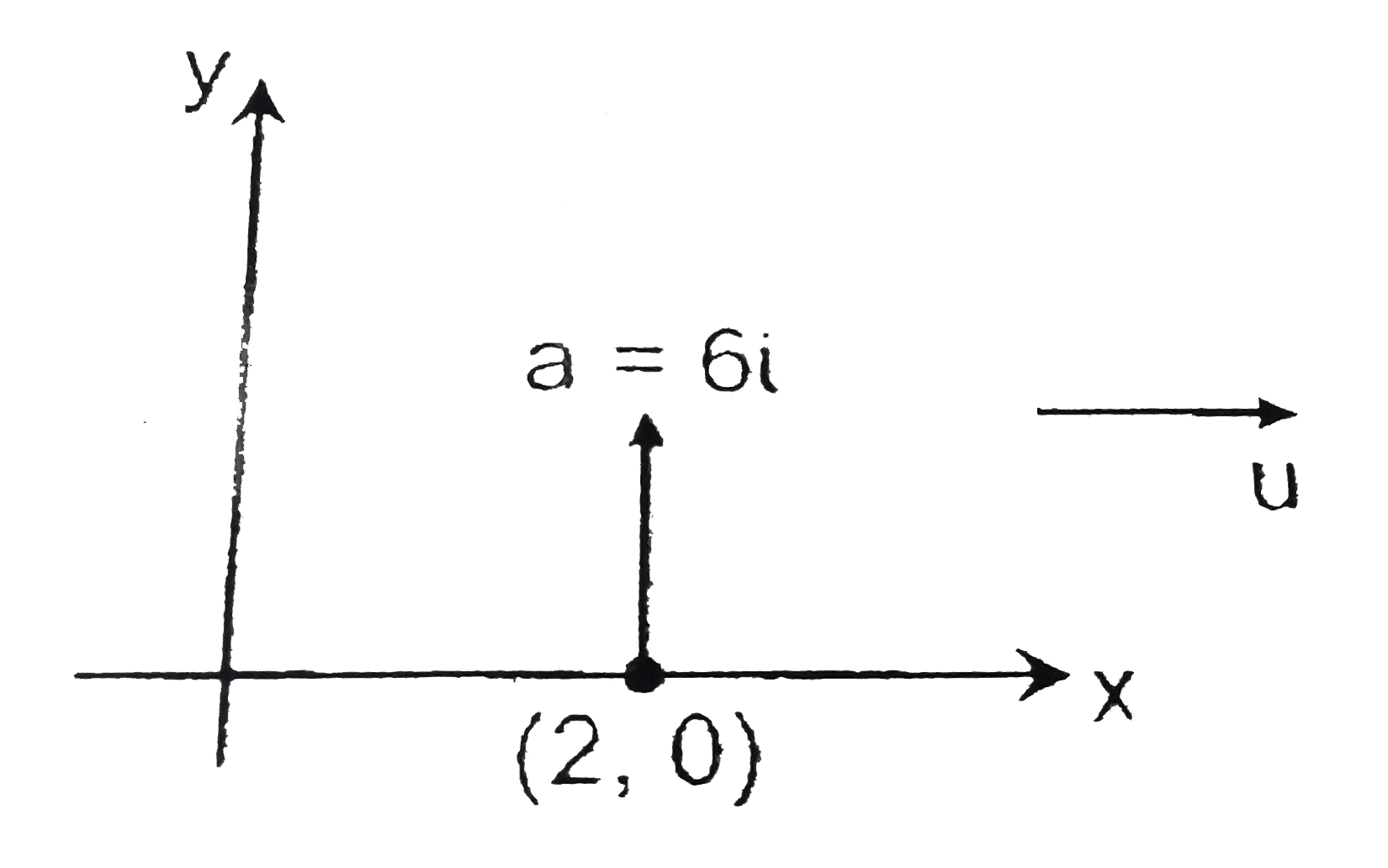
A boat starting from rest aims perpendicular to the river with an acceleration of $a = 6 t$
(where $t =$ time) the boat starts from $(2, 0)$ of the coordinate system. Find equation of trajectory. Given velocity of river $= u$ .
A $(x - 2) = u y^{\frac{2}{3}}$
B $x - 2 = u y^{\frac{1}{3}}$
C $x - 2 = u y^{\frac{1}{3}} y$
D $x - 2 = u^{\frac{2}{3}} y$
Velocity of water in a river is
ASame everywhere
BMore in the middle and less near its banks
CLess in the middle and more near its banks
DIncrease from one bank to other bank
The velocity of image w.r.t ground in the below figure is

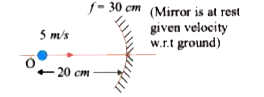A45 m/s and approaches the mirror
B45 m/s and moves away from the mirror
C60 m/s and approaches the mirror
D60 m/s and moves away from the mirror